1. treeMap,treesSet 作用:1具有对应普通的Map,Set的功能,2.能排序Map和Set (依赖树的结构进行排序---中序循环)
TreeSet<String> treeSet=new TreeSet<String>(); treeSet.add("2"); treeSet.add("1"); treeSet.add("5"); treeSet.add("3"); treeSet.add("1"); treeSet.comparator(); System.out.println(treeSet); TreeSet<Person> persons=new TreeSet<Person>(); persons.add(new Person("zhou",29)); persons.add(new Person("cao",30)); persons.add(new Person("jiao",29)); System.out.println(treeSet);
问题:TreeMap的key对象和TreeSet里的元素 在 Tree没有比较器的时候,必须要实现 Comparable 这个接口 否则会报错。
final int compare(Object k1, Object k2) { return comparator==null ? ((Comparable<? super K>)k1).compareTo((K)k2) : comparator.compare((K)k1, (K)k2); }
2.二叉树的编译分析 参照 https://blog.csdn.net/qq_40772692/article/details/79343914
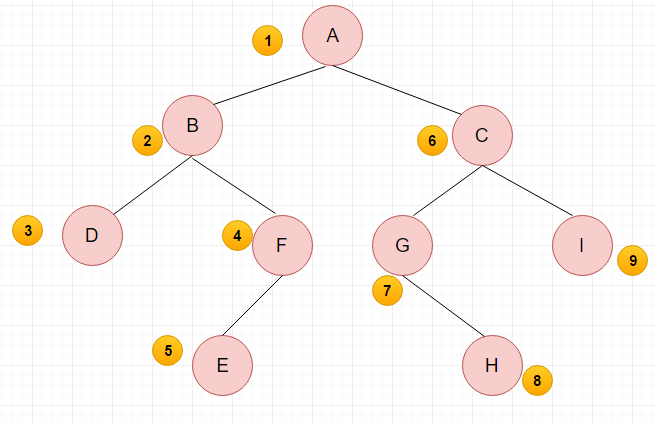
先序遍历:(1)访问根节点;(2)采用先序递归遍历左子树;(3)采用先序递归遍历右子树;
(注:每个节点的分支都遵循上述的访问顺序,体现“递归调用”)
先序遍历结果:A BDFE CGHI
思维过程:(1)先访问根节点A,
(2)A分为左右两个子树,因为是递归调用,所以左子树也遵循“先根节点-再左-再右”的顺序,所以访问B节点,
(3)然后访问D节点,
(4)访问F节点的时候有分支,同样遵循“先根节点-再左--再右”的顺序,
(5)访问E节点,此时左边的大的子树已经访问完毕,
(6)然后遵循最后访问右子树的顺序,访问右边大的子树,右边大子树同样先访问根节点C,
(7)访问左子树G,
(8)因为G的左子树没有,所以接下俩访问G的右子树H,
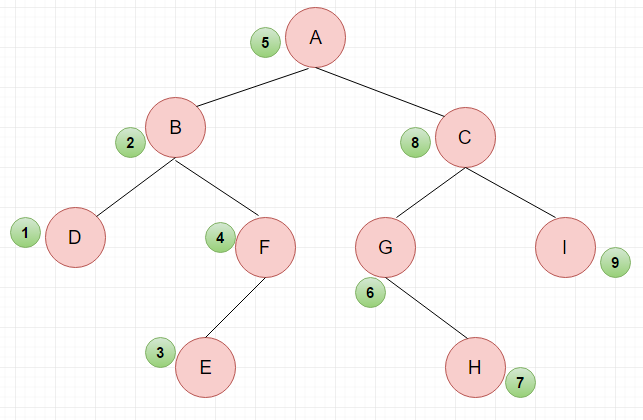
中序遍历:(1)采用中序遍历左子树;(2)访问根节点;(3)采用中序遍历右子树
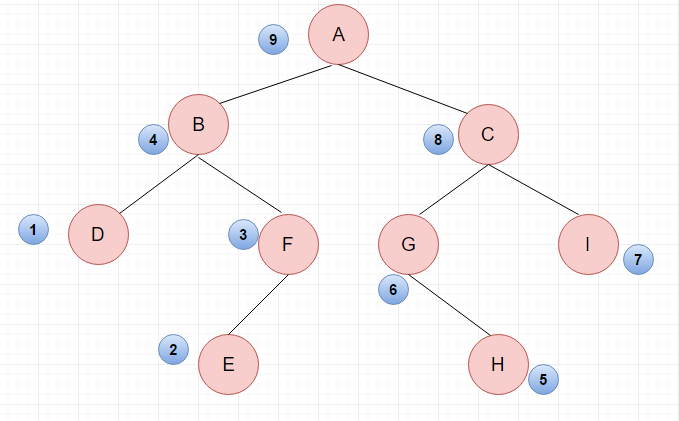
后序遍历的结果:DEFB HGIC A
小结:三种方法遍历过程中经过节点的路线一样;只是访问各个节点的时机不同。
3. LongAdder
原理:把long 求和分成了 很多cells,每个线程操作的求和,在每个线程对应的cell里进行,这样,就能减少高并发时的碰撞 类似concurrentHashMap
用途:用在高并发求和,如果在高并发的过程中调用sum() 会发生重复(因为求和和加减的过程没有加锁),这不是他的缺点,设计如此。
换句话说,如果在高并发的最后获取值 用LongAdder 如果在并发过程中,就需要操作这个数,只能用AtomicLong
原因: AtomicLong 使用了cas 直接更新值,并返回,返回的结果肯定就是当前的值。而 LongAdder 的sum()只是简单的求和。
4.bitset
java.util.BitSet可以按位存储。
计算机中一个字节(byte)占8位(bit),我们java中数据至少按字节存储的,
比如一个int占4个字节。
如果遇到大的数据量,这样必然会需要很大存储空间和内存。
如何减少数据占用存储空间和内存可以用算法解决。
java.util.BitSet就提供了这样的算法。
比如有一堆数字,需要存储,source=[3,5,6,9]
用int就需要4*4个字节。
java.util.BitSet可以存true/false。
如果用java.util.BitSet,则会少很多,其原理是:
1,先找出数据中最大值maxvalue=9
2,声明一个BitSet bs,它的size是maxvalue+1=10
3,遍历数据source,bs[source[i]]设置成true.
最后的值是:
(0为false;1为true)
bs [0,0,0,1,0,1,1,0,0,1]
3, 5,6, 9
这样一个本来要int型需要占4字节共32位的数字现在只用了1位!
比例32:1
这样就省下了很大空间。
package com; import java.util.BitSet; public class MainTestThree { /** * @param args */ public static void main(String[] args) { BitSet bm=new BitSet(); System.out.println(bm.isEmpty()+"--"+bm.size()); bm.set(0); System.out.println(bm.isEmpty()+"--"+bm.size()); bm.set(1); System.out.println(bm.isEmpty()+"--"+bm.size()); System.out.println(bm.get(65)); System.out.println(bm.isEmpty()+"--"+bm.size()); bm.set(65); System.out.println(bm.isEmpty()+"--"+bm.size()); } }
输出:
true--64
false--64
false--64
false
false--64
false--128
bitSet实现原理:
Long 为8个字节,最长的基本类型。一共64位可以放置 64个不同的数字。
Long[] 为实现原理,根据最大的数确定 有几个long可以实现。
System.out.println(1<<6);
System.out.println((64-1)>>6);
public void set(int bitIndex) { if (bitIndex < 0) throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex); int wordIndex = wordIndex(bitIndex); expandTo(wordIndex); words[wordIndex] |= (1L << bitIndex); // Restores invariants checkInvariants(); }
public void clear(int bitIndex) { if (bitIndex < 0) throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex); int wordIndex = wordIndex(bitIndex); if (wordIndex >= wordsInUse) return; words[wordIndex] &= ~(1L << bitIndex); recalculateWordsInUse(); checkInvariants(); }
5.bitarray
bitarray和bitset原理类型。但是 bitarray可以获取对应位为1的值。而bitSet只是单纯的去重。
6.BloomFilter
在计算机这个领域里,我们常常碰到时间换空间或空间换时间的情况,为了达到某一方面的性能,牺牲另外一方面。BloomFilter在时间和空间着两者之间引入了另外一个概念——错误率。也就是前文提到的布隆过滤不能准确判断一个元素是否在集合内(类似的设计还有基数统计法)。引入错误率后,极大的节省了存储空间。
private static int size = 1000000; private static BloomFilter<Integer> bloomFilter = BloomFilter.create(Funnels.integerFunnel(), size); public static void main(String[] args) { for (int i = 0; i < size; i++) { bloomFilter.put(i); } for (int i = 0; i < size; i++) { if (!bloomFilter.mightContain(i)) { System.out.println("有坏人逃脱了"); } } List<Integer> list = new ArrayList<Integer>(1000); for (int i = size + 10000; i < size + 200000; i++) { if (bloomFilter.mightContain(i)) { list.add(i); } } System.out.println("有误伤的数量:" + list.size());