题目描述:
给定一个字符串 s1,我们可以把它递归地分割成两个非空子字符串,从而将其表示为二叉树。

在扰乱这个字符串的过程中,我们可以挑选任何一个非叶节点,然后交换它的两个子节点。
例如,如果我们挑选非叶节点 "gr" ,交换它的两个子节点,将会产生扰乱字符串 "rgeat" 。
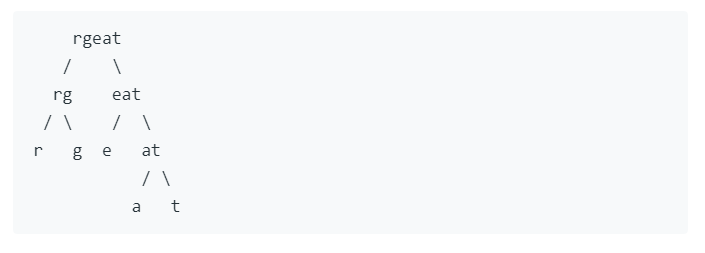
我们将 "rgtae” 称作 "great" 的一个扰乱字符串。给出两个长度相等的字符串 s1 和 s2,判断 s2 是否是 s1 的扰乱字符串。
题解:扰乱的过程实际上是划分子区间的过程,考虑区间dp。定义dp[l][i][j]表示s1从i开始,s2从j开始长度为l的区间是否为扰乱区间。
状态转移的过程也不能,对于长度为l的区间,依次选取分割点,按照题目的规则划分子区间即可(具体看代码)
AC代码:
bool isScramble(string s1, string s2) { int Len1 = s1.length(); int Len2 = s2.length(); if(Len1 != Len2 ) return false; int dp[Len1+5][Len1+5][Len1+5]; for(int i=0;i<=Len1;i++) { for(int j=0;j<=Len2;j++) { for(int k=0;k<=Len2;k++) dp[i][j][k] = 0; } }
// init() for(int i=0;i<Len1;i++) { for(int j=0;j<Len2;j++) { if(s1[i] == s2[j]) dp[1][i][j] = 1; } } for(int l=2;l<=Len1;l++) { for(int i=0;i+l-1<Len1;i++) { for(int j=0;j+l-1<Len1;j++) { for(int k=1;k<=l;k++) {
//正常比对 if(dp[k][i][j] == 1 && dp[l-k][i+k][j+k] == 1) dp[l][i][j] = 1;
//扰乱之后的比对 if(dp[k][i][j+l-k] == 1 && dp[l-k][i+k][j] == 1) dp[l][i][j] = 1; } } } } return dp[Len1][0][0]; }