zoukankan html css js c++ java

A 第三课贪心算法

内容概述及预备知识

预备知识：钞票支付问题：

代码实现：

#include <iostream>
using namespace std;

int main(){
    const int RMB[] = {200,100,20,10,5,1};
    int kinds = sizeof(RMB)/sizeof(RMB[0]); // 6 中面额 
    int money = 628;
    int total = 0;

    for(int i=0;i<kinds;i++){
        int cnt = money / RMB[i]; // 计算面额为RMB[i] 所需要的张数  
        total += cnt;
        money -= cnt*RMB[i];
        cout << "需要面额为" << RMB[i] <<" "<<cnt<<"张" << endl; 
        cout << "剩余要支付的金额是: " <<money<< endl;
    }
    cout <<"总共需要"<<total<<"张"<< endl;

    return 0;
}

/*

需要面额为200 3张
剩余要支付的金额是: 28
需要面额为100 0张
剩余要支付的金额是: 28
需要面额为20 1张
剩余要支付的金额是: 8
需要面额为10 0张
剩余要支付的金额是: 8
需要面额为5 1张
剩余要支付的金额是: 3
需要面额为1 3张
剩余要支付的金额是: 0
总共需要8张


*/

View Code

比如要支付14块钱，（按上面贪心算法所述，拿1个10块，4个1块[5个]），其实2个7块即可，所以贪心就不成立了，（如何解决呢？动态规划）

例1：分糖果（LeetCode No.455）

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个孩子 i ，都有一个胃口值 gi ，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j ，都有一个尺寸 sj 。如果 sj >= gi ，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

注意：

你可以假设胃口值为正。
一个小朋友最多只能拥有一块饼干。

思路及代码：

思考：

1，用小糖果满足即可，

2，满足需求小的即可，

代码实现：

#include <iostream>
#include <vector>
#include <algorithm> // for sort()
using namespace std;

void print(vector<int> &vec){
    for(auto it = vec.cbegin();it!= vec.cend();it++){
        cout <<*it<<" ";
    }
    cout << endl;
}

int findContentChildren(vector<int>& g, vector<int>& s) {
    // 先对 g  和 s 排序  
    sort(g.begin(),g.end());
    sort(s.begin(),s.end());
    
    int gIdx=0;int gSize = g.size();
    int sIdx=0;int sSize = s.size();
    int res = 0;
    while(1){
        // 遍历糖果
        if(gIdx>gSize-1|| sIdx>sSize -1){
            break;
        }
        if(s[sIdx]>=g[gIdx]){// sIdx 满足了 gIdx  
            res++;
            gIdx++;
            sIdx++;
        }else{ // sIdx 没有满足 gIdx  
            sIdx++;
        }
    }

    return res;
}

int main(){

    vector<int> g = {2,5,9,9,10,15};
    vector<int> s = {1,3,6,8,20};
    int ret = findContentChildren(g,s);
    cout << ret<< endl;


    return 0;
}

View Code

#include <iostream>
#include <vector>
#include <algorithm> // for sort()
using namespace std;

void print(vector<int> &vec){
    for(auto it = vec.cbegin();it!= vec.cend();it++){
        cout <<*it<<" ";
    }
    cout << endl;
}

int findContentChildren(vector<int>& g, vector<int>& s) {
    // 先对 g  和 s 排序  
    sort(g.begin(),g.end());
    sort(s.begin(),s.end());
    
    int gIdx=0;int gSize = g.size();
    int sIdx=0;int sSize = s.size();
    while(gIdx <= gSize-1 && sIdx <=sSize -1){ //gIdx 和 sIdx 都要在范围之内
        if(s[sIdx]>=g[gIdx]){// sIdx 满足了 gIdx  
            gIdx++;
        } 
        sIdx++; // sIdx 满足不满足 gIdx ,sIdx 都要向后移动一个  
    }

    return gIdx;
}

int main(){

    vector<int> g = {2,5,9,9,10,15};
    vector<int> s = {1,3,6,8,20};
    int ret = findContentChildren(g,s);
    cout << ret<< endl;


    return 0;
}

更简洁的代码

例2：摇摆序列（LeetCode No.376）

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

思路及代码：

思考：

贪心规律：

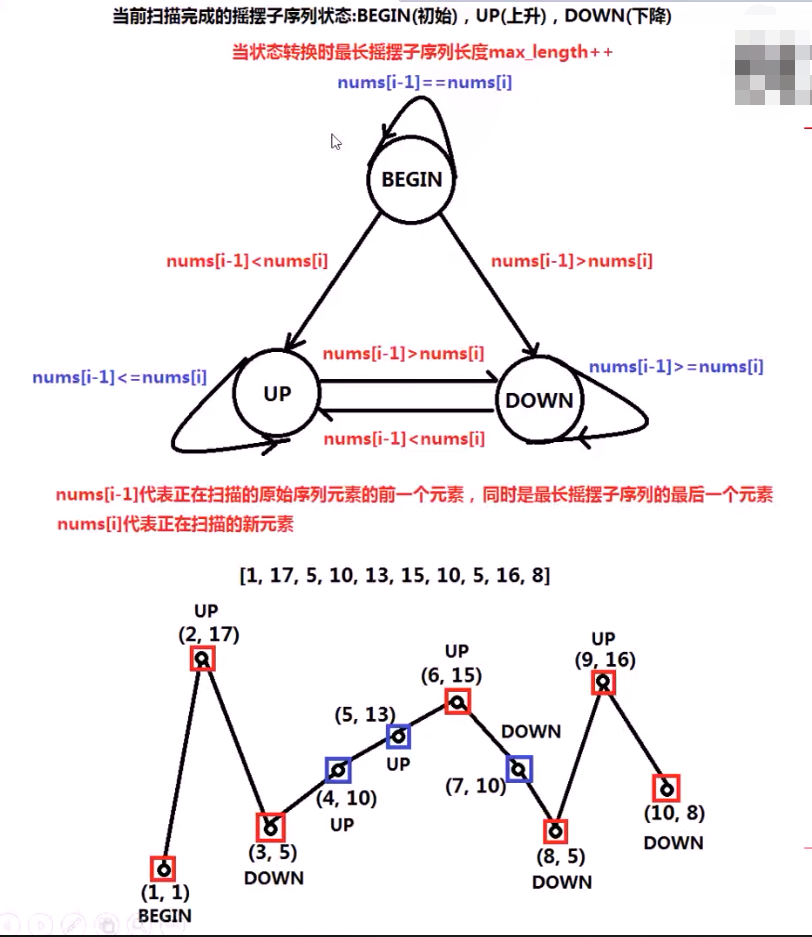
代码：

#include <iostream>
#include <vector>

using namespace std;

int wiggleMaxLength(vector<int>& nums) {
    int size = nums.size();

    if(size == 0)
        return 0;

    int maxLen = 1;
    int oldState = 0;
    int newState = 0; // 0 begin 1 up -1 down
    for(int i=0;i< size;i++){
        if(i-1 <0)
            continue;
        // 初始化
        if(newState == 0){
            if(nums[i-1]< nums[i]){
                newState = 1; // up 
                maxLen ++;
            }else if(nums[i-1]>nums[i]){
                newState = -1; // down
                maxLen ++;
            }
            continue;
        }

        // 状态不一样
        if(newState != oldState){
            if(newState == 1){ // 上升 
                if(nums[i-1] < nums[i]){
                    oldState = newState;
                }else if(nums[i-1]>nums[i]){
                    oldState = newState;
                    newState = -1;
                    maxLen++;
                }
            }else{ // 下降 
                if(nums[i-1] < nums[i]){
                    oldState = newState;
                    newState = 1;
                    maxLen++;
                }else if(nums[i-1]>nums[i]){
                    oldState = newState;
                }
            }
        }else{
            if(newState >0 ){ //上升状态 
                if(nums[i-1] > nums[i]){
                    maxLen ++;
                    newState = -1;
                }
            }else if(newState <0 ){ // 下降
                if(nums[i-1] < nums[i]){
                    maxLen ++;
                    newState = 1;
                }
            }
         }
    }
    

    return maxLen;
}

int main(){

    //vector<int> vec = {1,17,5,10,13,15,10,5,16,8};
    //vector<int> vec = {1,2,3,4,5,6,7,8,9};
    //vector<int> vec = {1,7,4,9,2,5};
    
    //vector<int> vec = {};
    //vector<int> vec = {1,3};
    
    //vector<int> vec = {1,1,2};
    //vector<int> vec = {1,1,7,4,9,2,5};
    //vector<int> vec = {1,2,2,2};
    //vector<int> vec = {2,2,2};
    vector<int> vec = {1,17,5,10,13,15,10,5,16,8};
    int ret = wiggleMaxLength(vec);
    cout << ret << endl;

    return 0;
}

我自己的

#include <iostream>
#include <vector>

using namespace std;

int wiggleMaxLength(vector<int>& nums) {
    if(nums.size() < 2 ){
        return nums.size();
    }
    int size = nums.size();

    int maxLen = 1;
    int state = 0; // 0 begin 1 up -1 down

    for(int i=1;i< size;i++){
        switch(state){
            case 0: // begin 
                if(nums[i-1]<nums[i]){ // 上升 
                    maxLen++;
                    state = 1;
                }else if(nums[i-1]>nums[i]){ // 下降  
                    maxLen++;
                    state = -1;
                }
                break;
            case 1:// up 
                if(nums[i-1]>nums[i]){ // 下降  
                    maxLen++;
                    state = -1;
                }
                break;
            case -1:// down
                if(nums[i-1]<nums[i]){ // 上升 
                    maxLen++;
                    state = 1;
                }
                break;
        }
    }
    return maxLen;
}

int main(){

    //vector<int> vec = {1,17,5,10,13,15,10,5,16,8};
    //vector<int> vec = {1,2,3,4,5,6,7,8,9};
    //vector<int> vec = {1,7,4,9,2,5};
    
    //vector<int> vec = {};
    //vector<int> vec = {1,3};
    
    //vector<int> vec = {1,1,2};
    //vector<int> vec = {1,1,7,4,9,2,5};
    //vector<int> vec = {1,2,2,2};
    //vector<int> vec = {2,2,2};
    vector<int> vec = {1,17,5,10,13,15,10,5,16,8};
    int ret = wiggleMaxLength(vec);
    cout << ret << endl;

    return 0;
}

老师代码

例3：移除k个数字（LeetCode No.402）

给定一个以字符串表示的非负整数 num，移除这个数中的 k 位数字，使得剩下的数字最小。

注意:

num 的长度小于 10002 且 ≥ k。
num 不会包含任何前导零。
示例 1 :

输入: num = "1432219", k = 3
输出: "1219"
解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。
示例 2 :

输入: num = "10200", k = 1
输出: "200"
解释: 移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。
示例 3 :

输入: num = "10", k = 2
输出: "0"
解释: 从原数字移除所有的数字，剩余为空就是0。

思路及代码：

思考：

贪心规律：

算法思路：

对于num = 1432219

具体思路：

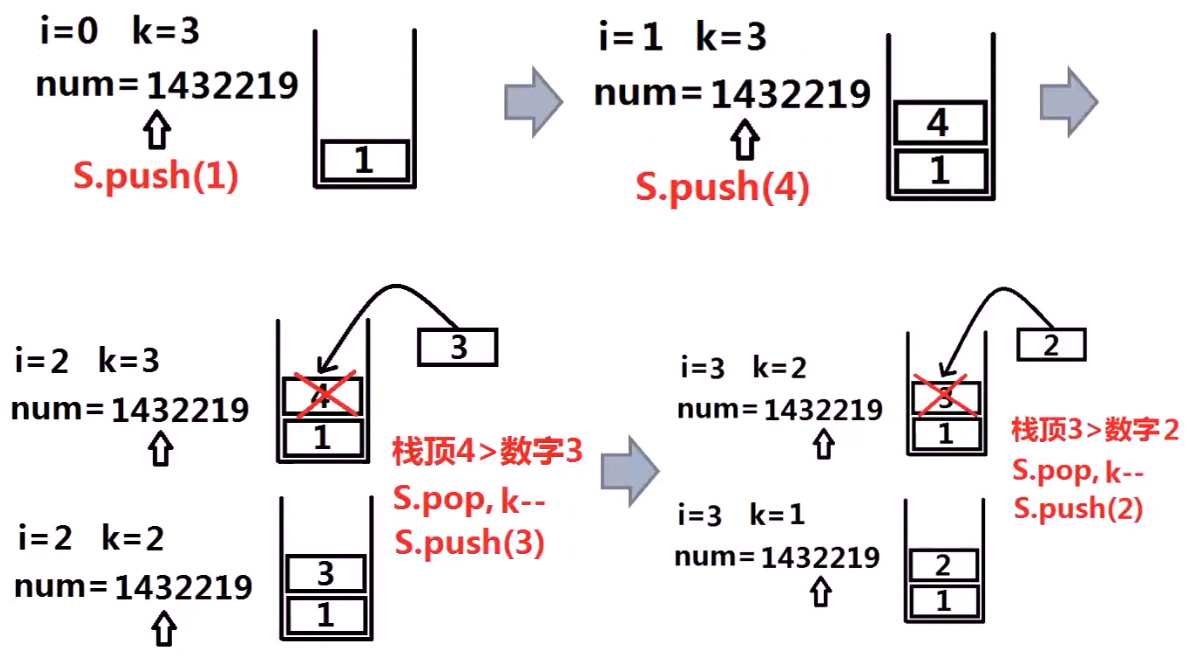
思考：

#include <iostream>
#include <string>
#include <vector> // 使用vector 做栈 因为vector 可以遍历

using namespace std;

string removeKdigits(string num, int k) {
    int len = num.length();

    vector<char> stk;
    string res = "";

    // 删除k个数字 // pop 栈 k次
    for(int i=0;i< len;i++){
        while(stk.size()>0 && k>0 && num[i] <stk[stk.size()-1]){//num[i] 小于 栈顶
            stk.pop_back();
            k--;
        }
        if(stk.size() == 0 && num[i] == '0'){ // num = 100200 ,k=1  
            continue;
        }
        stk.push_back(num[i]);
    }
    if(k>0){  // num =12345,k = 3;
        for(int i=0;i<k;i++){
            stk.pop_back();
        }
    }

    for(int i=0;i<(int)stk.size();i++){
        res.append(1,stk[i]);
    }
    if(res == ""){
        return "0";
    }
        
    return res;
}


int main(){
    string s = "1234567890";
    string ret = removeKdigits(s,9);
    cout << ret << endl;

    return 0;
}

View Code

#include <iostream>
#include <string>
#include <vector> // 使用vector 做栈 因为vector 可以遍历

using namespace std;

string removeKdigits(string num, int k) {
    int len = num.length();
    if(k == 0){
        return num;
    }
    if(len == k){
        return "0";
    }

    vector<char> stk;
    string res = "";

    // 删除k个数字 // pop 栈 k次
    for(int i=0;i< len;i++){
        while(stk.size()>0 && k>0 && num[i] <stk[stk.size()-1]){//num[i] 小于 栈顶
            stk.pop_back();
            k--;
        }
        if(stk.size() == 0 && num[i] == '0'){ // num = 100200 ,k=1  
            continue;
        }
        stk.push_back(num[i]);
    }
    if(k>0){  // num =12345,k = 3;
        for(int i=0;i<k;i++){
            stk.pop_back();
        }
    }

    for(int i=0;i<(int)stk.size();i++){
        res.append(1,stk[i]);
    }
    if(res == ""){
        return "0";
    }
        
    return res;
}


int main(){
    string s = "1234567890";
    string ret = removeKdigits(s,9);
    cout << ret << endl;

    return 0;
}

好一点

例4:跳跃游戏（LeetCode No.55）

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 1:

输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
示例 2:

输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ，所以你永远不可能到达最后一个位置。

思路及代码：

思考：

贪心规律：

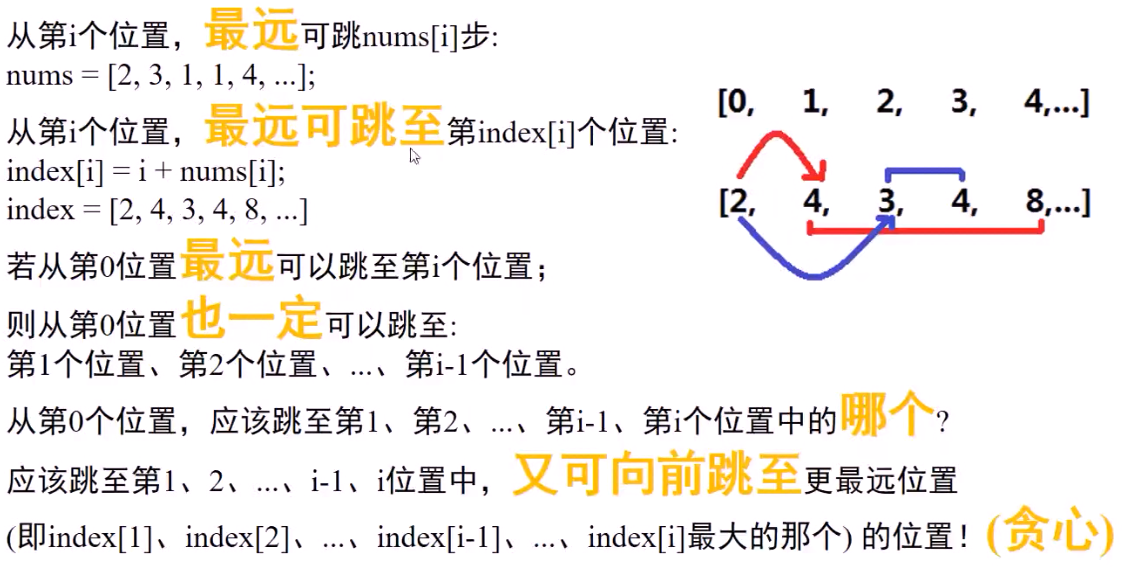
我的代码：

#include <iostream>
#include <vector>

using namespace std;

bool canJump(vector<int>& nums) {
    int size = nums.size();
    vector<int> maxIdx; // nums[i] 最大能跳到的位置 
    for(int i=0;i<size;i++){
        maxIdx.push_back(i+nums[i]);
    }
    int jumpIdx = 0; 
    int targetPos;// 要跳的位置
    while(1){
        if(nums[jumpIdx] == 0){
            break;
        }else{
            targetPos = jumpIdx+1;
        }

        for(int i=jumpIdx+2;i<= min(maxIdx[jumpIdx],size-1);i++){
            if(maxIdx[targetPos]<maxIdx[i]){
                targetPos = i;
            }
        }
        cout << targetPos<< endl;
        jumpIdx = targetPos;
        if(targetPos >= size-1){
            break;
        }
    }
    return jumpIdx >= size -1;
}

int main(){
    //vector<int> vec = {2,3,1,1,4};
    //           masIdx = 2 4 3 4 8  
    
    vector<int> vec = {2,0};
    bool ret = canJump(vec);
    cout <<"res: "<< ret << endl;




    return 0;
}

View Code

老师思路：

#include <iostream>
#include <vector>

using namespace std;

bool canJump(vector<int>& nums) {
    int size = nums.size();
    vector<int> maxIdx; // nums[i] 最大能跳到的位置 
    for(int i=0;i<size;i++){
        maxIdx.push_back(i+nums[i]);
    }
    int curIdx = 0; 
    int maxJumpIdx = maxIdx[0];
    while(curIdx < size &&  curIdx <= maxJumpIdx){
        if(maxJumpIdx < maxIdx[curIdx]){
            maxJumpIdx = maxIdx[curIdx];
        }
        curIdx++;
    }

    return curIdx == size;
}

int main(){
    //vector<int> vec = {2,3,1,1,4};
    //           masIdx = 2 4 3 4 8  
    
    
    vector<int> vec = {2,0};
    bool ret = canJump(vec);
    cout <<"res: "<< ret << endl;




    return 0;
}

View Code

例4-b:跳跃游戏（LeetCode No.45）

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。
说明:

假设你总是可以到达数组的最后一个位置。

思路及代码：

思路和上题一致，

我的代码：

#include <iostream>
#include <vector>

using namespace std;


int jump(vector<int>& nums) {
    int size = nums.size();
    if(size == 0 || size == 1)
        return 0;
    if(size == 2)
        return 1;
    vector<int> maxIdx; // nums[i] 最大能跳到的位置 
    for(int i=0;i<size;i++){
        maxIdx.push_back(i+nums[i]);
    }
    int jumpIdx = 0; 
    int targetPos;// 要跳的位置
    int cnt = 0; // 要跳几次 
    while(1){
        targetPos = jumpIdx+1;
        for(int i=jumpIdx+2;i<= min(maxIdx[jumpIdx],size-1);i++){
            if(maxIdx[targetPos] <= maxIdx[i] || i== size-1){
                targetPos = i;
            }
        }
        cout << targetPos<< endl;
        jumpIdx = targetPos;
        cnt++;
        if(targetPos >= size-1){
            break;
        }
    }
    return cnt;
}

int main(){
    //vector<int> vec = {2,3,1,1,4};
    //        maxIdx = 2 4 3 4 8  
    
    
    //vector<int> vec = {2,0};
    //vector<int> vec = {3,2,1};
    vector<int> vec = {2,3,1};
    
    int ret = jump(vec);
    cout <<"res: "<< ret << endl;




    return 0;
}

View Code

例5:射击气球（LeetCode No.452）

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以y坐标并不重要，因此只要知道开始和结束的x坐标就足够了。开始坐标总是小于结束坐标。平面内最多存在10^4个气球(好像没用)。

一支弓箭可以沿着x轴从不同点完全垂直地射出。在坐标x处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend，且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

Example:

输入:
[[10,16], [2,8], [1,6], [7,12]]

输出:
2

解释:

对于该样例，我们可以在x = 6（射爆[2,8],[1,6]两个气球）和 x = 11（射爆另外两个气球）。

思路及代码：

贪心规律：

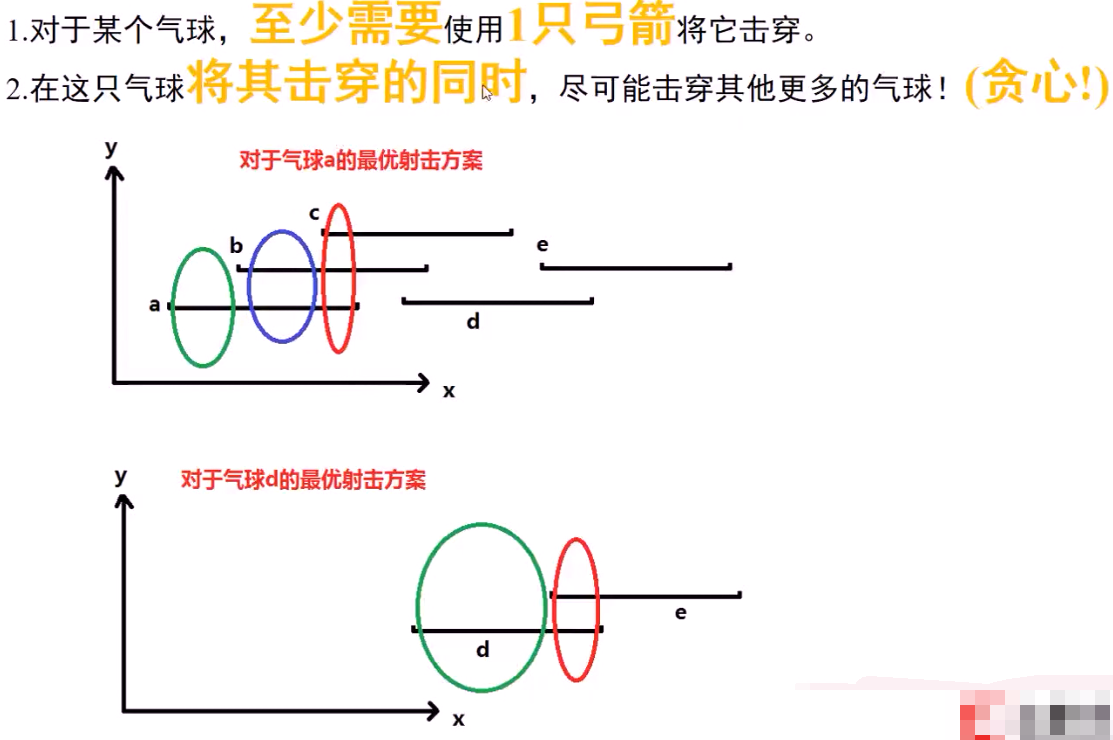
算法思路：

具体思路：

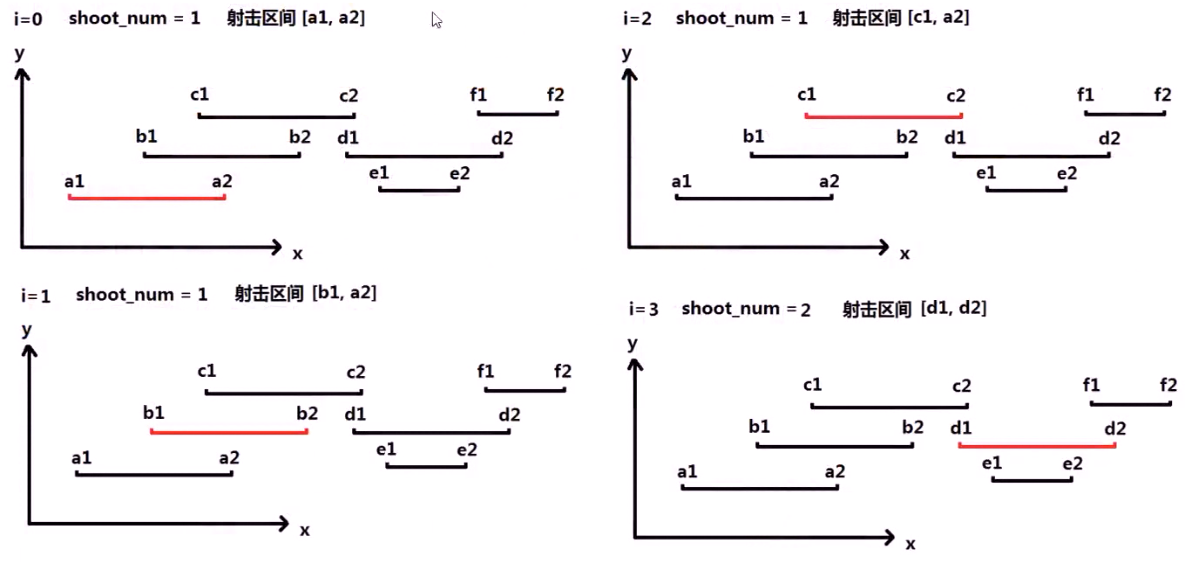
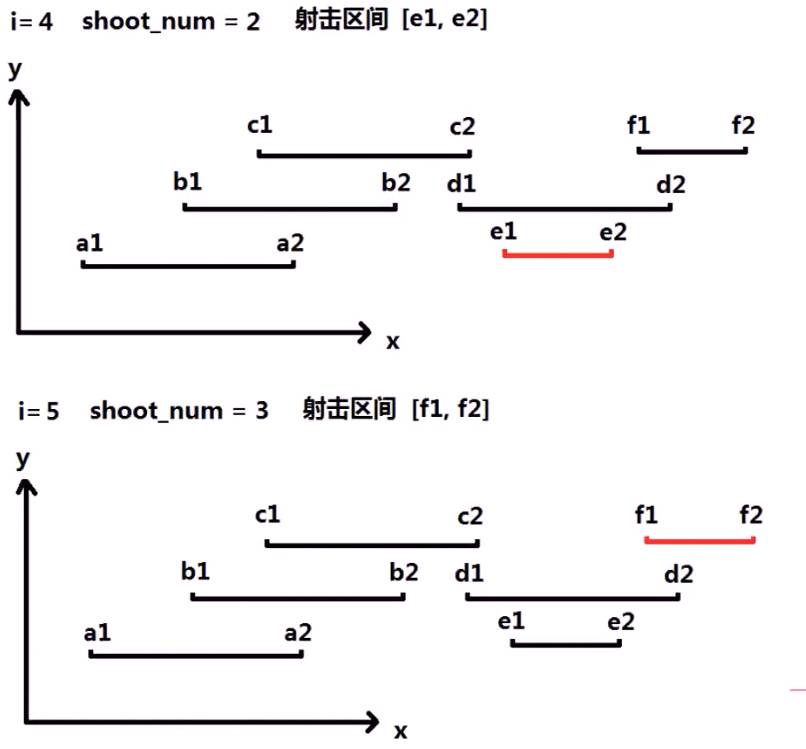
代码：

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

bool cmp(vector<int> &a,vector<int> &b){
    return a[0] < b[0]; // 无序考虑 左面端点相同的排序
}

int findMinArrowShots(vector<vector<int>>& points) {
    if(points.size() == 0)
        return 0;
    sort(points.begin(),points.end(),cmp);

    int shootNum = 1; // 初始化 弓箭手数量为 1
    int shootBegin = points[0][0];//  初始化 设计区间
    int shootEnd = points[0][1]; 

    int size = points.size();
    for(int i=1;i<size;i++){
        if(points[i][0] <= shootEnd){// 当新气球的左 < 射击区间右,更新当前的设计区间
            shootBegin = points[i][0];
            if(shootEnd > points[i][1]){ // 当射击区间 右 > 新气球的右
                shootEnd = points[i][1];
            }
        }else{ // 需要增加 新的射击区间 
            shootNum++;
            shootBegin = points[i][0];
            shootEnd = points[i][1];
        }
    }
        
    return shootNum;
}

int main(){
    vector<vector<int>> vecs;
    vector<int> vec1 = {10,16};
    vector<int> vec2 = {2,8};
    vector<int> vec3 = {1,6};
    vector<int> vec4 = {7,12};
    vecs.push_back(vec1);
    vecs.push_back(vec2);
    vecs.push_back(vec3);
    vecs.push_back(vec4);

    int ret = findMinArrowShots(vecs);
    cout << ret << endl;


    return 0;
}

View Code

例6:最优加油方法（poj No.2341）

思考和代码：

贪心规律：

算法思路：

代码：

#include <iostream>
#include <algorithm>
#include <vector>
#include <queue> // for priority_queue
using namespace std;

bool cmp(vector<int> &a,vector<int> &b){
    return a[0] > b[0]; 
}

int getMinStop(int L,int P,vector<vector<int>> &stop){ //L为起点到终点的距离, P为起点初始的汽油量 // vector[0] 是加油站距终点的距离 vector[1] 是加油站最多加的汽油量  

    
    priority_queue<int> heap;  // 存储各个加油站最大加油量的 最大堆  
    int res = 0; // 加油的次数
    vector<int> temp;
    temp.push_back(0);
    temp.push_back(0);
    stop.push_back(temp); // 终点 Push 到stop中,终点也作为一个停靠点

    sort(stop.begin(),stop.end(),cmp); // 以停靠点至 终点的距离进行从大到小排序 

    int size = stop.size();
    for(int i=0;i<size;i++){
        int dis = L -stop[i][0];
        while(P<dis && heap.size() > 0){
            P += heap.top(); // 加油  
            heap.pop();
            res++;
        }
        if(P<dis && heap.size() == 0)
            return  -1;

        P = P - dis;
        L = stop[i][0];
        heap.push(stop[i][1]); // 将该停靠点 加入最大堆 
    }
    return res;
}
int main(){

    vector<vector<int>> vecs;
    int N;
    int L; 
    int P;
    int distance;
    int fuel;
    scanf("%d",&N); // 几个 加油站 
    for(int i =0;i<N;i++){
        scanf("%d %d",&distance,&fuel); // 加油站 距离终点的 距离和最大油量
        vector<int> temp;
        temp.push_back(distance);
        temp.push_back(fuel);
        vecs.push_back(temp);
    }
    scanf("%d %d",&L,&P); // 初始时 的距离 和 油量

    cout << getMinStop(L,P,vecs)<< endl;

    return 0;
}

View Code

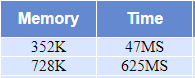
其中627Ms 是上面代码，

更好代码：

#include <iostream>
#include <algorithm>
#include <vector>
#include <queue> // for priority_queue

using namespace std;

bool cmp(pair<int,int>&a,pair<int,int>&b){
    return a.first > b.first; 
}

int getMinStop(int L,int P,vector<pair<int,int>> &stop){ //L为起点到终点的距离, P为起点初始的汽油量 // vector[0] 是加油站距终点的距离 vector[1] 是加油站最多加的汽油量  

    
    priority_queue<int> heap;  // 存储各个加油站最大加油量的 最大堆  
    int res = 0; // 加油的次数
    stop.push_back(make_pair(0,0)); // 终点 Push 到stop中,终点也作为一个停靠点

    sort(stop.begin(),stop.end(),cmp); // 以停靠点至 终点的距离进行从大到小排序 

    int size = stop.size();
    for(int i=0;i<size;i++){
        int dis = L -stop[i].first;
        while(P<dis && heap.size() > 0){
            P += heap.top(); // 加油  
            heap.pop();
            res++;
        }
        if(P<dis && heap.size() == 0)
            return  -1;

        P = P - dis;
        L = stop[i].first;
        heap.push(stop[i].second); // 将该停靠点 加入最大堆 
    }
    return res;
}
int main(){

    vector<pair<int,int>> vecs;
    int N;
    int L; 
    int P;
    int distance;
    int fuel;
    scanf("%d",&N); // 几个 加油站 
    for(int i =0;i<N;i++){
        scanf("%d %d",&distance,&fuel); // 加油站 距离终点的 距离和最大油量
        vector<int> temp;
        vecs.push_back(make_pair(distance,fuel));
    }
    scanf("%d %d",&L,&P); // 初始时 的距离 和 油量
    cout << getMinStop(L,P,vecs)<< endl;

    return 0;
}

View Code

这个代码是 47Ms ，可见换个数据结构影响是多么大，

查看全文

相关阅读:
javascript高级知识分析——灵活的参数
 javascript高级知识分析——实例化
 javascript高级知识分析——上下文
 javascript高级知识分析——作为对象的函数
 javascript高级知识分析——函数访问
 javascript高级知识分析——定义函数
 new到底做了什么？
JavaScript中的计时器原理
 解析Function.prototype.bind
将类数组对象(array-like object)转化为数组对象(Array object)

原文地址：https://www.cnblogs.com/zach0812/p/13647594.html

最新文章
POJ 2492
POJ 2485
POJ 2487
POJ 2470
POJ 2453
POJ 2418
POJ 2421
POJ 2436
POJ 2410
POJ 2405

A 第三课 贪心算法

内容概述及预备知识

预备知识：钞票支付问题：

例1：分糖果（LeetCode No.455）

思路及代码：

例2：摇摆序列（LeetCode No.376）

思路及代码：

例3：移除k个数字（LeetCode No.402）

思路及代码：

例4:跳跃游戏（LeetCode No.55）

思路及代码：

例4-b:跳跃游戏（LeetCode No.45）

思路及代码：

例5:射击气球（LeetCode No.452）

思路及代码：

例6:最优加油方法（poj No.2341）

思考和代码：

A 第三课贪心算法