自古逢秋悲寂寥,我言秋日胜春朝。
晴空一鹤排云上,便引诗情到碧霄。 ——刘禹锡
题目:推箱子
网址:http://poj.org/problem?id=1475
推箱子游戏相信大家都不陌生,在本题中,你将控制一个人把1个箱子到目的地。
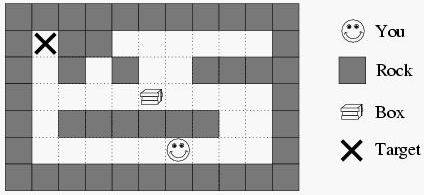
给定一张N行M列的地图,用字符”.”表示空地,字符”#”表示墙,字符”S”表示人的起始位置,字符”B”表示箱子的起始位置,字符”T”表示箱子的目标位置。
求一种移动方案,使箱子移动的次数最少,在此基础上再让人移动的总步数最少。
方案中使用大写的“EWSN”(东西南北)表示箱子的移动,使用小写的“ewsn”(东西南北)表示人的移动。
输入格式
输入包含多个测试用例。
对于每个测试用例,第一行包括两个整数N,M。
接下来N行,每行包括M个字符,用以描绘整个N行M列的地图。
当样例为N=0,M=0时,表示输入终止,且该样例无需处理。
输出格式
对于每个测试用例,第一行输出”Maze #”+测试用例的序号。
第二行输入一个字符串,表示推箱子的总体移动过程,若无解,则输出”Impossible.”。
每个测试用例输出结束后输出一个空行。
若有多条路线满足题目要求,则按照N、S、W、E的顺序优先选择箱子的移动方向(即先上下推,再左右推)。
在此前提下,再按照n、s、w、e的顺序优先选择人的移动方向(即先上下动,再左右动)。
数据范围
1≤N,M≤20
输入样例:
1 7
SB....T
1 7
SB..#.T
7 11
###########
#T##......#
#.#.#..####
#....B....#
#.######..#
#.....S...#
###########
8 4
....
.##.
.#..
.#..
.#.B
.##S
....
###T
0 0
输出样例:
Maze #1
EEEEE
Maze #2
Impossible.
Maze #3
eennwwWWWWeeeeeesswwwwwwwnNN
Maze #4
swwwnnnnnneeesssSSS
这道题有点难,我们不妨可以这样考虑进行假设:
- 若没有箱子,我们可以使用广搜求出人到任意一点的最短距离;
题意明确要求先保证箱子步数最小,再保证人走的路程最短,并要给出具体方案;
先考虑如何保证箱子步数最小,或者说如何求解这个最小值呢?
考虑状态(box_x, box_y, man_x, man_y),对于该状态进行广度优先搜索即可。
我们考虑,请试想:该状态扩展时,会扩展出什么呢?箱子显然不可能向任意方向扩展,只有当人在箱子的一侧,将其“向前”推到符合题意的位置(无障碍),进行一次扩展操作;人的扩展可以枚举四个方向,每次扩展到没有障碍的位置时,将新状态放于队尾进行扩展。
这样,当箱子处于目标位置即为最小值了。
你做错了! !
还记得广度优先搜索满足什么性质吗?单调性。
那么,队列中什么满足单调性呢?状态满足单调性。那么,我们刚刚的做法,实际上是以总步数作为关键字,总步数单调!
而实际上题目要求箱子移动步数最优的前提下再保证人步数最小值。换言之,箱子移动步数是第一关键字,而在此满足最优的情况下,人作为第二关键表示在状态中了。
那么,对于每个状态,我们只能定义关于箱子的位置,而并不能带上人的坐标。
对于人走了多少步,我们可以在对其中进行BFS扩展;
总结:对于推箱子这个问题,其实是箱子走迷宫问题,状态的每一次扩展时所需要的人最少步数,恰又是一个BFS。
大的BFS套着一个BFS,这便是所谓的“双重BFS”!
其实,不管题目有多么复杂,如果每次考虑问题都先整体去考虑,对于细节的求解假定它是可求的,那么,当大框架大部署确定后,问题便一目了然,无论是算法设计还是代码实现。
代码如下:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<stack>
#include<queue>
#define pii pair <int , int>
//To simplify the questions, we prefer to use pair and make first -> x, second -> y.
#define x first
#define y second
using namespace std;
struct rec
{
int x, y, dir;
} man, box, tg;
//tg -> target
const int MAX_size = 20 + 10;
const int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, -1, 1};
const char cdir[5] = {'N', 'S', 'W', 'E', '�'}, ddir[5] = {'n', 's', 'w', 'e', '�'}; //up 0 down 1 left 2 right 3
queue <char> ans;
bool book[MAX_size][MAX_size][4];
bool mat[MAX_size][MAX_size];
char map[MAX_size][MAX_size];
int n, m;
int d[MAX_size][MAX_size], d_man[MAX_size][MAX_size][4], f_box[MAX_size][MAX_size][4], d_box[MAX_size][MAX_size][4];
int f_man[MAX_size][MAX_size];
void init()
{
memset(f_man, -1, sizeof(f_man));
memset(f_box, -1, sizeof(f_box));
memset(d_man, -1, sizeof(d_man));
memset(d_box, -1, sizeof(d_box));
memset(mat, false, sizeof(mat));
memset(book, false, sizeof(book));
for(int i = 1; i <= n; ++ i)
{
for(int j = 1; j <= m; ++ j)
{
if(map[i][j] == 'S')man.x = i, man.y = j;
else if(map[i][j] == 'B')box.x = i, box.y = j;
else if(map[i][j] == 'T')tg.x = i, tg.y = j, tg.dir = -1;
}
}
return;
}
bool valid(int x, int y)
{
if(x < 1 || x > n || y < 1 || y > m || map[x][y] == '#') return 0;
return 1;
}
int expand(pii st, pii ed, stack <char> &s)
{
queue <pii> Q;
while(!s.empty()) s.pop();
while(!Q.empty()) Q.pop();
if(st.x == ed.x && st.y == ed.y) return 0;
Q.push(st);
mat[st.x][st.y] = true;
d[st.x][st.y] = 0;
while(!Q.empty())
{
pii now = Q.front(), next;
Q.pop();
for(int k = 0; k < 4; ++ k)
{
next = make_pair(now.x + dx[k], now.y + dy[k]);
if(!valid(next.x, next.y) || mat[next.x][next.y]) continue;
f_man[next.x][next.y] = k;
mat[next.x][next.y] = true;
d[next.x][next.y] = d[now.x][now.y] + 1;
if(next.x == ed.x && next.y == ed.y)
{
int prev_x = next.x, prev_y = next.y, tmp_1, tmp_2;
while(!(prev_x == st.x && prev_y == st.y))
{
s.push(ddir[f_man[prev_x][prev_y]]);
tmp_1 = prev_x - dx[f_man[prev_x][prev_y]];
tmp_2 = prev_y - dy[f_man[prev_x][prev_y]];
prev_x = tmp_1, prev_y = tmp_2;
}
return d[next.x][next.y];
}
Q.push(next);
}
}
return -1;
}
void _print(int x, int y, int dir)
{
stack <char> s;
if(x == box.x && y == box.y && f_box[x][y][dir] == -1)
{
mat[box.x][box.y] = true;
expand(make_pair(man.x, man.y), make_pair(box.x - dx[dir], box.y - dy[dir]), s);
memset(mat, false, sizeof(mat));
while(!s.empty())
{
ans.push(s.top());
s.pop();
}
return;
}
int prev_dir = f_box[x][y][dir], prev_x = x - (dx[dir] + dx[prev_dir]), prev_y = y - dy[dir] - dy[prev_dir];
_print(x - dx[dir], y - dy[dir], prev_dir);
mat[x - dx[dir]][y - dy[dir]] = true;
expand(make_pair(prev_x, prev_y), make_pair(x - (dx[dir] * 2), y - (dy[dir] * 2)), s);
memset(mat, false, sizeof(mat));
while(!s.empty())
{
ans.push(s.top());
s.pop();
}
ans.push(cdir[dir]);
return;
}
bool bfs()
{
queue <rec> Q;
stack <char> s;
while(!Q.empty()) Q.pop();
int k;
for(k = 0; k < 4; ++ k)
{
int &num = d_box[box.x][box.y][k], &cnt = d_man[box.x][box.y][k];
if(!valid(box.x - dx[k], box.y - dy[k])) continue;
mat[box.x][box.y] = true;
cnt = expand(make_pair(man.x, man.y), make_pair(box.x - dx[k], box.y - dy[k]), s);
memset(mat, false, sizeof(mat));
if(cnt == -1) continue;
Q.push(rec {box.x, box.y, k});
book[box.x][box.y][k] = true;
num = 0;
}
while(!Q.empty())
{
rec now = Q.front(), next;
Q.pop();
for(k = 0; k < 4; ++ k)
{
next.x = now.x + dx[k];
next.y = now.y + dy[k];
next.dir = k;
if(!valid(next.x, next.y)) continue;
int &num = d_box[next.x][next.y][k], &cnt = d_man[next.x][next.y][k] , tmp;
mat[now.x][now.y] = true;
tmp = expand(make_pair(now.x - dx[now.dir], now.y - dy[now.dir]), make_pair(now.x - dx[k], now.y - dy[k]), s);
memset(mat, false, sizeof(mat));
if(tmp == -1) continue;
if(book[next.x][next.y][next.dir])
{
if(num >= d_box[now.x][now.y][now.dir] + 1 && cnt > tmp + d_man[now.x][now.y][now.dir])
{
num = d_box[now.x][now.y][now.dir] + 1;
cnt = d_man[now.x][now.y][now.dir] + tmp;
f_box[next.x][next.y][k] = now.dir;
}
continue;
}
book[next.x][next.y][k] = true;
f_box[next.x][next.y][next.dir] = now.dir;
num = d_box[now.x][now.y][now.dir] + 1;
cnt = d_man[now.x][now.y][now.dir] + tmp;
if(next.x == tg.x && next.y == tg.y)
{
if(tg.dir == -1)
tg.dir = next.dir;
else
{
if(num > d_box[tg.x][tg.y][tg.dir])
{
_print(tg.x, tg.y, tg.dir);
return true;
}
else if(cnt < d_man[tg.x][tg.y][tg.dir]) tg.dir = next.dir;
}
}
Q.push(next);
}
}
if(tg.dir != -1)
{
_print(tg.x, tg.y, tg.dir);
return true;
}
return false;
}
int main()
{
int T = 1;
while(scanf("%d %d", &n, &m) == 2 && n && m)
{
printf("Maze #%d
", (T ++));
for(int i = 1; i <= n; ++ i)
{
scanf("%s", map[i] + 1);
}
init();
if(bfs())
{
while(!ans.empty())
{
printf("%c", ans.front());
ans.pop();
}
puts("");
}
else puts("Impossible.");
puts("");
}
return 0;
}