题目链接:https://abc042.contest.atcoder.jp/tasks/arc058_b
题目大意:
给定一个 H * W 的矩阵,其中左下角 A * B 区域是禁区,要求在不踏入禁区的前提下,从左上角走到右下角一共有多少种走法?
分析:
设 D 为往下,R为往左。
这里举个 H = 10,W = 7,A = 3,B = 4的例子:
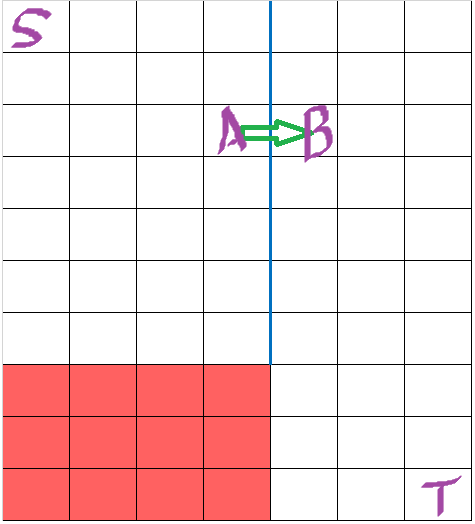
首先不管怎么走,路线都是要跨越蓝色边界线的,这里我们只讨论从 A 跨越到 B 的情况,其余情况同理。
在这种情况下,总的路数就是所有从 S 走到 A 的路线总数乘上所有从 B 走到 T 的路线总数。
从 S 走到 A 的路线总数就是组合数 C(5, 2),这是因为从 S 走到 A 需要走2个 D 和3个 R,也就是说,2个 D 和3个 L 能组合出多少不同的序列,这是非常基本的组合题,答案就是5个里选2个即 C(5, 2)。
同理从 B 走到 T 的路线总数为 C(9, 2)。
于是这种情况下的总路数为 C(5, 2) * C(9, 2)。
找一下规律把所有情况加起来即可,注意数据规模很大,所以在求组合数时要用到逆元。
代码如下:

1 #pragma GCC optimize("Ofast") 2 #include <bits/stdc++.h> 3 using namespace std; 4 5 #define INIT() std::ios::sync_with_stdio(false);std::cin.tie(0); 6 #define Rep(i,n) for (int i = 0; i < (n); ++i) 7 #define For(i,s,t) for (int i = (s); i <= (t); ++i) 8 #define rFor(i,t,s) for (int i = (t); i >= (s); --i) 9 #define ForLL(i, s, t) for (LL i = LL(s); i <= LL(t); ++i) 10 #define rForLL(i, t, s) for (LL i = LL(t); i >= LL(s); --i) 11 #define foreach(i,c) for (__typeof(c.begin()) i = c.begin(); i != c.end(); ++i) 12 #define rforeach(i,c) for (__typeof(c.rbegin()) i = c.rbegin(); i != c.rend(); ++i) 13 14 #define pr(x) cout << #x << " = " << x << " " 15 #define prln(x) cout << #x << " = " << x << endl 16 17 #define LOWBIT(x) ((x)&(-x)) 18 19 #define ALL(x) x.begin(),x.end() 20 #define INS(x) inserter(x,x.begin()) 21 22 #define ms0(a) memset(a,0,sizeof(a)) 23 #define msI(a) memset(a,inf,sizeof(a)) 24 #define msM(a) memset(a,-1,sizeof(a)) 25 26 #define MP make_pair 27 #define PB push_back 28 #define ft first 29 #define sd second 30 31 template<typename T1, typename T2> 32 istream &operator>>(istream &in, pair<T1, T2> &p) { 33 in >> p.first >> p.second; 34 return in; 35 } 36 37 template<typename T> 38 istream &operator>>(istream &in, vector<T> &v) { 39 for (auto &x: v) 40 in >> x; 41 return in; 42 } 43 44 template<typename T1, typename T2> 45 ostream &operator<<(ostream &out, const std::pair<T1, T2> &p) { 46 out << "[" << p.first << ", " << p.second << "]" << " "; 47 return out; 48 } 49 50 typedef long long LL; 51 typedef unsigned long long uLL; 52 typedef pair< double, double > PDD; 53 typedef pair< int, int > PII; 54 typedef set< int > SI; 55 typedef vector< int > VI; 56 typedef map< int, int > MII; 57 const double EPS = 1e-10; 58 const int inf = 1e9 + 9; 59 const LL mod = 1e9 + 7; 60 const int maxN = 1e5 + 7; 61 const LL ONE = 1; 62 const LL evenBits = 0xaaaaaaaaaaaaaaaa; 63 const LL oddBits = 0x5555555555555555; 64 65 LL fac[2 * maxN]; 66 void init_fact() { 67 fac[0] = 1; 68 For(i, 1, 2 * maxN - 1) { 69 fac[i] = (i * fac[i - 1]) % mod; 70 } 71 } 72 73 //ax + by = gcd(a, b) = d 74 // 扩展欧几里德算法 75 inline void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){ 76 if (!b) {d = a, x = 1, y = 0;} 77 else{ 78 ex_gcd(b, a % b, y, x, d); 79 y -= x * (a / b); 80 } 81 } 82 83 // 求a关于p的逆元,如果不存在,返回-1 84 // a与p互质,逆元才存在 85 inline LL inv_mod(LL a, LL p){ 86 LL d, x, y; 87 ex_gcd(a, p, x, y, d); 88 return d == 1 ? (x % p + p) % p : -1; 89 } 90 91 // Calculate x^y % p 92 inline LL pow_mod(LL x, LL y, LL p){ 93 LL ans = 1; 94 while(y){ 95 if(y & 1) ans = (ans * x) % p; 96 x = (x * x) % p; 97 y >>= 1; 98 } 99 return ans; 100 } 101 102 inline LL comb_mod(LL m,LL n){ 103 LL ans; 104 if(m > n) swap(m, n); 105 106 ans = (fac[n] * inv_mod(fac[m], mod)) % mod; 107 ans = (ans * inv_mod(fac[n - m], mod)) % mod; 108 109 return ans; 110 } 111 112 int H, W, A, B; 113 LL ans; 114 115 int main(){ 116 INIT(); 117 init_fact(); 118 cin >> H >> W >> A >> B; 119 For(i, 1, H - A) { 120 ans += (comb_mod(i - 1, i + B - 2) * comb_mod(W - B - 1, W - B + H - i - 1)) % mod; 121 ans %= mod; 122 } 123 124 cout << ans << endl; 125 return 0; 126 }
