题目链接:HDU-6057
题意:

思路:先按照官方题解推导出下面的式子:

现在唯一的问题就是怎么解决[bit(x)-bit(y)=bit(k)]的问题。
我们定义( F(A,k)_{i}=left[ bitleft( i ight) =k ight] * A_{i} ),相当于把A、B、C分别按照bit划分成m+1个序列。
有如下公式:
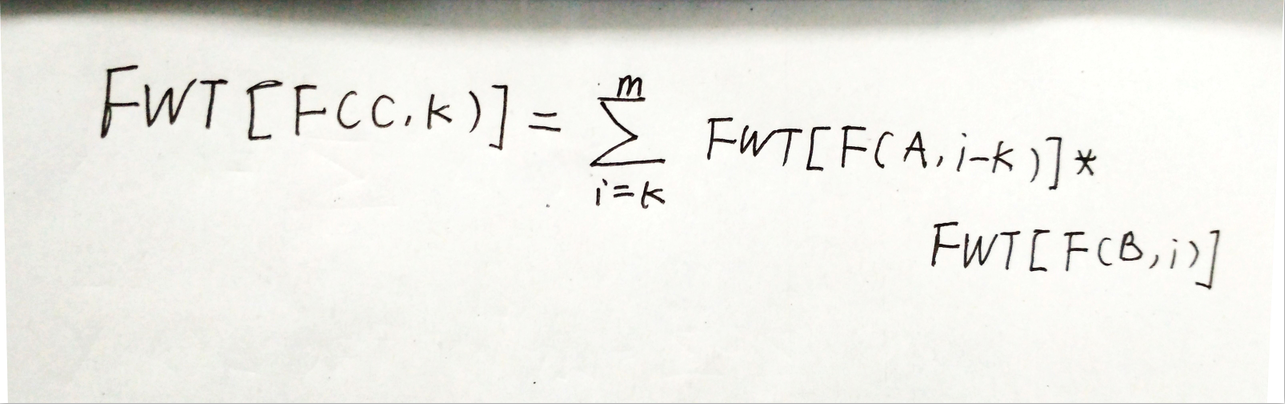
同时我们发现( C_k=F(C,bit(k)))_k )。
然后我们就可以搞出来啦!
代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 using namespace std; 6 typedef long long LL; 7 8 const LL MAXN=600010; 9 const LL MOD=998244353; 10 LL A[32][MAXN],B[32][MAXN],C[32][MAXN]; 11 LL two[32]; 12 LL bit(LL x) 13 { 14 LL ret=0; 15 while(x>0) 16 { 17 if(x&1) ret++; 18 x>>=1; 19 } 20 return ret; 21 } 22 // 快速幂 23 // 求x^n%mod 24 // Verified! 25 LL powMod(LL x,LL n,LL mod) 26 { 27 LL res=1; 28 while(n>0) 29 { 30 if(n&1) res=res*x % mod; 31 x=x*x % mod; 32 n>>=1; 33 } 34 return res; 35 } 36 LL inv(LL a,LL m) 37 { 38 return powMod(a,m-2,m); 39 // return powMod(a,eularPhi(m)-1,m); 40 } 41 LL inv2; 42 void FWT_Xor(LL *A, LL len) { 43 if (len == 1) return; 44 LL len2 = len >> 1; 45 FWT_Xor(A, len2); 46 FWT_Xor(A + len2, len2); 47 for (LL i = 0; i < len2; ++i) { 48 LL x = A[i], y = A[i + len2]; 49 A[i] = (x + y) % MOD; 50 A[i + len2] = ((((x - y) % MOD) + MOD) % MOD); 51 } 52 } 53 void IFWT_Xor(LL *A, LL len) { 54 if (len == 1) return; 55 LL len2 = len >> 1; 56 for (LL i = 0; i < len2; ++i) { 57 LL x = A[i], y = A[i + len2]; 58 A[i] = ((x + y) % MOD) * inv2 % MOD; 59 A[i + len2] = ((((x - y) % MOD) + MOD) % MOD) * inv2 % MOD; 60 } 61 IFWT_Xor(A, len2); 62 IFWT_Xor(A + len2, len2); 63 } 64 int main() 65 { 66 #ifdef LOCAL 67 freopen("in.txt","r",stdin); 68 #endif 69 inv2=inv(2,MOD); 70 memset(A,0,sizeof(A)); 71 memset(B,0,sizeof(B)); 72 memset(C,0,sizeof(C)); 73 two[0]=1; 74 for(LL i=1;i<32;i++) two[i]=two[i-1]*2%MOD; 75 76 LL m; 77 scanf("%lld",&m); 78 for(LL i=0;i<(1<<m);i++) 79 { 80 LL x; 81 scanf("%lld",&x); 82 A[bit(i)][i]=x*two[bit(i)]%MOD; 83 } 84 for(LL i=0;i<(1<<m);i++) 85 { 86 LL x; 87 scanf("%lld",&x); 88 B[bit(i)][i]=x; 89 } 90 for(LL i=0;i<=m;i++) FWT_Xor(A[i],(1<<m)); 91 for(LL i=0;i<=m;i++) FWT_Xor(B[i],(1<<m)); 92 for(LL k=0;k<=m;k++) 93 for(LL i=k;i<=m;i++) 94 for(LL j=0;j<(1<<m);j++) 95 C[k][j]=(C[k][j]+A[i-k][j]*B[i][j])%MOD; 96 for(LL i=0;i<=m;i++) IFWT_Xor(C[i],(1<<m)); 97 LL ans=0,mi=1; 98 for(LL i=0;i<(1<<m);i++) 99 { 100 ans=(ans+C[bit(i)][i]*mi)%MOD; 101 mi=mi*1526%MOD; 102 } 103 printf("%lld ",ans); 104 return 0; 105 }