noip模拟赛 同余方程组

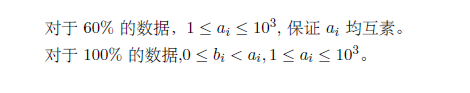
分析：这道题一个一个枚举都能有70分......

      前60分可以用中国剩余定理搞一搞.然而并没有枚举分数高......考虑怎么省去不必要的枚举，每次跳都只跳a的倍数,这样对前面的式子没有影响,为了使得这个倍数最小从而不会WA掉，每次跳最小公倍数就可以了.

 60分代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

ll mod[5], a[5], ans, M = 1;

void exgcd(ll a, ll b, ll &x, ll &y)
{
    if (!b)
    {
        x = 1;
        y = 0;
        return;
    }
    exgcd(b, a % b, x, y);
    ll t = x;
    x = y;
    y = t - (a / b) * y;
    return;
}

int main()
{
    scanf("%lld%lld%lld%lld%lld%lld%lld%lld", &mod[1], &a[1], &mod[2], &a[2], &mod[3], &a[3], &mod[4], &a[4]);
    for (int i = 1; i <= 4; i++)
        M *= mod[i];
    for (int i = 1; i <= 4; i++)
    {
        ll mi = M / mod[i];
        ll x, y;
        exgcd(mi, mod[i], x, y);
        ans = (ans + a[i] * mi * x) % M;
    }
    if (ans < 0)
        ans += M;
    printf("%lld
", ans);

    return 0;
}

100分代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

ll mod[5], a[5], gcd, lcm, ans;

ll GCD(ll x, ll y)
{
    if (!y)
        return x;
    return GCD(y, x % y);
}

int main()
{
    scanf("%lld%lld%lld%lld%lld%lld%lld%lld", &mod[1], &a[1], &mod[2], &a[2], &mod[3], &a[3], &mod[4], &a[4]);
    lcm = mod[1];
    gcd = mod[1];
    ans = a[1];
    for (int i = 2; i <= 4; i++)
    {
        while (ans % mod[i] != a[i])
            ans += lcm;
        gcd = GCD(gcd, mod[i]);
        lcm = lcm / gcd * mod[i];
    }
    printf("%lld
", ans);

    return 0;
}