2597: [Wc2007]剪刀石头布
Time Limit: 20 Sec Memory Limit: 128 MBSec Special JudgeSubmit: 1765 Solved: 763
[Submit][Status][Discuss]
Description
在一些一对一游戏的比赛(如下棋、乒乓球和羽毛球的单打)中,我们经常会遇到A胜过B,B胜过C而C又胜过A的有趣情况,不妨形象的称之为剪刀石头布情况。有的时候,无聊的人们会津津乐道于统计有多少这样的剪刀石头布情况发生,即有多少对无序三元组(A, B, C),满足其中的一个人在比赛中赢了另一个人,另一个人赢了第三个人而第三个人又胜过了第一个人。注意这里无序的意思是说三元组中元素的顺序并不重要,将(A, B, C)、(A, C, B)、(B, A, C)、(B, C, A)、(C, A, B)和(C, B, A)视为相同的情况。
有N个人参加一场这样的游戏的比赛,赛程规定任意两个人之间都要进行一场比赛:这样总共有场比赛。比赛已经进行了一部分,我们想知道在极端情况下,比赛结束后最多会发生多少剪刀石头布情况。即给出已经发生的比赛结果,而你可以任意安排剩下的比赛的结果,以得到尽量多的剪刀石头布情况。
Input
输入文件的第1行是一个整数N,表示参加比赛的人数。
之后是一个N行N列的数字矩阵:一共N行,每行N列,数字间用空格隔开。
在第(i+1)行的第j列的数字如果是1,则表示i在已经发生的比赛中赢了j;该数字若是0,则表示在已经发生的比赛中i败于j;该数字是2,表示i和j之间的比赛尚未发生。数字矩阵对角线上的数字,即第(i+1)行第i列的数字都是0,它们仅仅是占位符号,没有任何意义。
输入文件保证合法,不会发生矛盾,当i≠j时,第(i+1)行第j列和第(j+1)行第i列的两个数字要么都是2,要么一个是0一个是1。
Output
输出文件的第1行是一个整数,表示在你安排的比赛结果中,出现了多少剪刀石头布情况。
输出文件的第2行开始有一个和输入文件中格式相同的N行N列的数字矩阵。第(i+1)行第j个数字描述了i和j之间的比赛结果,1表示i赢了j,0表示i负于j,与输入矩阵不同的是,在这个矩阵中没有表示比赛尚未进行的数字2;对角线上的数字都是0。输出矩阵要保证合法,不能发生矛盾。
Sample Input
3
0 1 2
0 0 2
2 2 0
0 1 2
0 0 2
2 2 0
Sample Output
1
0 1 0
0 0 1
1 0 0
0 1 0
0 0 1
1 0 0
HINT
100%的数据中,N≤ 100。
分析:挺妙的一道题!
直接想怎么构造最多的三元组很难. 反向思考. 用总的三元组的个数-最少的不合法的三元组的个数即为所求.
关键就是如何使得不合法的三元组最少.
首先要知道不合法的三元组有什么特征.画个图可以发现:一个不合法的三元组中必然有一个点,另外两个点指向它.那么答案就是
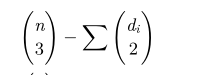 。
。
第一部分是一个定值,关键就是要使得第二部分最小.
每一条没有确定方向的边都只会对它连着的某一个点产生贡献,可以用容量表示数量的限制. 那么贡献是多少呢?
仔细分析,可以发现这其实是一个贡献递增的模型,类似bzoj1449,bzoj1070.每条边的费用只需要设为这一次的增量即可.
最后输出方案枚举每条边看是否满流即可.
反向思考是很重要的技巧!遇到这类问题,要求的东西的条件非常多/复杂,减去不符合条件的即可.
Tips:bzoj的spj好像有点问题?我的程序和标准输出会有差异,过了洛谷的官方数据在bzoj上会WA掉.
#include <cstdio> #include <queue> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int maxn = 110,maxm = 200010,inf = 0x3f3f3f3f,maxx = 20000; int n,a[maxn][maxn],pos[maxn][maxn],ans,S,T,tot = 2,cnt; int head[maxm],to[maxm],nextt[maxm],w[maxm],cost[maxm]; int vis[maxm],vis2[maxm],d[maxm]; void add(int x,int y,int z,int p) { w[tot] = z; cost[tot] = p; to[tot] = y; nextt[tot] = head[x]; head[x] = tot++; w[tot] = 0; cost[tot] = -p; to[tot] = x; nextt[tot] = head[y]; head[y] = tot++; } void pre() { S = maxx; T = S + 1; for (int i = 1; i <= n; i++) for (int j = 0; j < n - 1; j++) add(S,i,1,j); cnt = n; for (int i = 1; i <= n; i++) for (int j = 1; j < i; j++) { cnt++; add(cnt,T,1,0); if (a[i][j] == 0 || a[i][j] == 2) { pos[i][j] = tot; add(i,cnt,1,0); } if (a[i][j] == 1 || a[i][j] == 2) { pos[j][i] = tot; add(j,cnt,1,0); } } } bool spfa() { queue <int> q; memset(vis,0,sizeof(vis)); memset(vis2,0,sizeof(vis2)); memset(d,0x3f,sizeof(d)); d[S] = 0; vis[S] = 1; q.push(S); while (!q.empty()) { int u = q.front(); q.pop(); vis[u] = 0; for (int i = head[u]; i; i = nextt[i]) { int v = to[i]; if (w[i] && d[v] > d[u] + cost[i]) { d[v] = d[u] + cost[i]; if (!vis[v]) { vis[v] = 1; q.push(v); } } } } return d[T] < inf; } int dfs(int u,int f) { if (u == T) { ans -= f * d[u]; return f; } int res = 0; vis2[u] = 1; for (int i = head[u]; i; i = nextt[i]) { int v = to[i]; if (w[i] && !vis2[v] && d[v] == d[u] + cost[i]) { int temp = dfs(v,min(f - res,w[i])); w[i] -= temp; w[i ^ 1] += temp; res += temp; if (res == f) return res; } } return res; } void dinic() { while(spfa()) dfs(S,inf); } int main() { scanf("%d",&n); for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) scanf("%d",&a[i][j]); ans = n * (n - 1) * (n - 2) / 6; pre(); dinic(); printf("%d ",ans); for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { if(i==j) printf("0 "); else if (a[i][j] != 2) printf("%d ",a[i][j]); else printf("%d ",w[pos[i][j]]); } printf(" "); } return 0; }