题解
数据结构维护区间凸包
应该有一个非常裸的dp:记 (f_u) 代表节点 (u) 的答案,有 (f_u=min_{vin anc(u),dep_u-dep_vle l_u}f_v+ (dep_u-dep_v) imes p_u+q_u) 其中 (dep_u) 代表 (u) 到根的距离。
然后我们发现如果没有 (l_u) 的限制这就是是一个非常套路的斜率优化式,直接套树上斜率优化的板子即可。但是这里有这么一个条件,可是我们发现这个条件其实也是满足一个单调性的,直接二分找到第一个满足这个条件的决策点然后以这个点为决策二分的左端点即可。然后你就可以获得50分的好成绩(配合上暴力估计70分)。
问题是有可能出现满足条件的点但是不在凸包上,在凸包上的点不满足条件,而这个不在凸包上的点还是最优决策点。
比如说下面这张图:
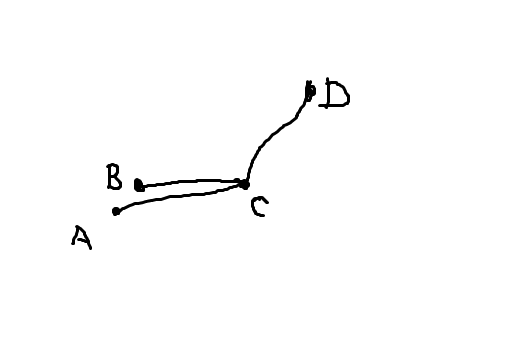
这里 A 不满足条件,但是 B 满足条件且为最优决策点。我们不难发现对于一个决策的可行决策点必然是一段区间,那么我们可以用线段树来维护(线段树上的下标是深度,而线段树所维护的其实是一条从当前点到根的链)。对于线段树上的每一个节点维护这个区间内的决策点所形成的凸壳。因为每个决策点只会在 (log{n}) 的节点内所以总空间复杂度为 (O(nlog{n})),然后对于查询在每个节点上二分找到当前节点的最优再在全部里选一个最优即可,时间复杂度 (O(log^2{n})),对于插入,每个决策点在 (log{n}) 个线段树上的节点只会插入删除各一次,所以之间复杂度均摊是 (O(log{n})) 的。
不难发现每个查询都是后缀,所以直接树状数组也可(还是线段树写得舒服)。每个节点维护凸壳的方法和树上斜率优化一样,要一个可撤销栈。
点分治
这道神仙题还可以点分治来做。
假设当前树的根是 (x),重心是 (y),那么我们考虑用 (x ightarrow y) 这条链上的点用斜率优化更新 (y) 的子树内的点。考虑条件 (dep[v]-dep[u]le l[v]),即 (dep[v]-l[v]le dep[u]),那么我们把子树内的点按 (dep[v]-l[v]),然后链上的点按 (dep) 从大到小排序。按顺序加入凸包(尺取)。这时我们就要保证 (x ightarrow y) 的点都算出了其的答案,我们可以先递归处理除了 (y) 的子树的部分,这样就得到了实现。
思路很简单写起来恶心得很(注意凸包维护的方向)。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const double inf = 1e18;
const int MAXN = 200005;
int n;
int fa[MAXN];
ll dep[MAXN], lim[MAXN], val[MAXN], p[MAXN], q[MAXN];
vector<int> vec[MAXN];
int stk[MAXN], top;
ll f[MAXN];
ll mini;
int rt;
int sz[MAXN];
bool vis[MAXN];
void get_root(int x, int tot_size) {
sz[x] = 1;
ll maxi = -inf;
for (auto y : vec[x]) {
if (vis[y]) continue;
get_root(y, tot_size);
sz[x] += sz[y];
maxi = max(maxi, (ll)sz[y]);
}
maxi = max(maxi, (ll)(tot_size - sz[x]));
// cout << x << " " << maxi << endl;
if ((mini > maxi) || (mini == maxi && dep[rt] > dep[x])) {
mini = maxi;
rt = x;
}
}
double X(int i) {
return dep[i];
}
double Y(int i) {
return f[i];
}
double slope(int i, int j) {
if (X(i) == X(j)) return Y(j) >= Y(i) ? inf : -inf;
return (Y(j) - Y(i)) / (X(j) - X(i));
}
void dfs1(int x) {
for (auto y : vec[x]) {
dep[y] = dep[x] + val[y];
dfs1(y);
}
}
struct Pair{
ll val, id;
friend bool operator < (Pair a, Pair b) {
return a.val > b.val;
}
}P[MAXN];
int num;
void dfs(int x) {
P[++num] = Pair{dep[x] - lim[x], x};
for (auto y : vec[x]) {
if (vis[y]) continue;
dfs(y);
}
}
void solve(int x, int size) {//处理根为 x,大小为 size 的子树
if (size == 1) return;//如果只有一个点直接返回就好了
mini = inf;
get_root(x, size);//找到重心 rt
if (mini >= inf) return;
int RT = rt;//因为 root 有可能更改所以存一下
for (auto y : vec[RT]) vis[y] = 1;//把 rt 的子树都打上标记,不让其下到 rt 的子树内
solve(x, size - sz[RT] + 1);//处理除了 rt 子树的其他部分
//此时从 x 到 rt 的链上的点的 dp 值已经处理出来了
num = 0;
for (auto y : vec[RT]) dfs(y);
sort(P + 1, P + 1 + num);//从大到小排序
int j = RT;
top = 0;
for (int i = 1; i <= num; i++) {
while (j != fa[x] && dep[j] >= P[i].val) {//决策点 j 是满足条件的,将决策点 j 加入凸包
while (top > 1 && slope(stk[top], stk[top - 1]) <= slope(j, stk[top])) top--;
stk[++top] = j;
j = fa[j];
}
//对 i 进行决策
if (top > 0) {
int l = 2, r = top, pos = 1;
while (l <= r)
{
int mid = (l + r) >> 1;
if (slope(stk[mid], stk[mid - 1]) >= p[P[i].id]) pos = mid, l = mid + 1;
else r = mid - 1;
}
pos = stk[pos];
f[P[i].id] = min(f[P[i].id], f[pos] + (dep[P[i].id] - dep[pos]) * p[P[i].id] + q[P[i].id]);
}
}
for (auto y : vec[RT]) solve(y, sz[y]);
}
int main() {
memset(f, 0x3f, sizeof(f));
f[1] = 0;
int T;
scanf("%d%d", &n, &T);
for (int i = 2; i <= n; i++) {
scanf("%d%lld%lld%lld%lld", fa + i, val + i, p + i, q + i, lim + i);
vec[fa[i]].push_back(i);
}
dfs1(1);
solve(1, n);
for (int i = 2; i <= n; i++) {
printf("%lld
", f[i]);
}
return 0;
}