【转】风控中的特征评价指标（二）——PSI

转自：https://zhuanlan.zhihu.com/p/79682292

风控业务背景

在风控中，稳定性压倒一切。原因在于，一套风控模型正式上线运行后往往需要很久（通常一年以上）才会被替换下线。如果模型不稳定，意味着模型不可控，对于业务本身而言就是一种不确定性风险，直接影响决策的合理性。这是不可接受的。

本文将从稳定性的直观理解、群体稳定性指标（Population Stability Index，PSI）的计算逻辑、PSI背后的含义等多维度展开分析。

目录
Part 1. 稳定性的直观理解
Part 2. 群体稳定性指标（Population Stability Index，PSI）的理解
Part 3. 相对熵（KL散度）的理解
Part 4. 相对熵与PSI之间的关系
Part 5. PSI指标的业务应用
Part 6. PSI的计算代码（Python）
致谢
版权声明
参考资料

Part 1. 稳定性的直观理解

在日常生活中，我们可能会看到每月电表、水表数值的变化。直观理解上的系统稳定，通常是指某项指标波动小（低方差），指标曲线几乎是一条水平的直线。此时，我们就会觉得系统运行正常稳定，很有安全感。

在数学上，我们通常可以用变异系数（Coefficient of Variation，CV）来衡量这种数据波动水平。变异系数越小，代表波动越小，稳定性越好。

变异系数的计算公式为：变异系数 C·V =（ 标准偏差 SD / 平均值Mean ）× 100%

那么，是不是只用用变异系数就可以了呢？方便、直观。——答案是否定的。在机器学习建模时，我们基于假设“历史样本分布等于未来样本分布”。因此，我们通常认为：

模型或变量稳定 <=> 未来样本分布与历史样本分布之间的偏差小。

然而，实际中由于受到客群变化（互金市场用户群体变化快）、数据源采集变化（比如爬虫接口被风控了）等等因素影响，实际样本分布将会发生偏移，就会导致模型不稳定。

Part 2. 群体稳定性指标（Population Stability Index，PSI）的理解

如果你有基础的风控建模经验，想必会很熟悉PSI（Population Stability Index）指标。PSI反映了验证样本在各分数段的分布与建模样本分布的稳定性。在建模中，我们常用来筛选特征变量、评估模型稳定性。

那么，PSI的计算逻辑是怎样的呢？很多博客文章都会直接告诉我们，稳定性是有参照的，因此需要有两个分布——实际分布（actual）和预期分布（expected）。其中，在建模时通常以训练样本（In the Sample, INS）作为预期分布，而验证样本通常作为实际分布。验证样本一般包括样本外（Out of Sample，OOS）和跨时间样本（Out of Time，OOT）。

我们从直觉上理解，是不是可以把两个分布重叠放在一起，比较下两个分布的差异有多大？

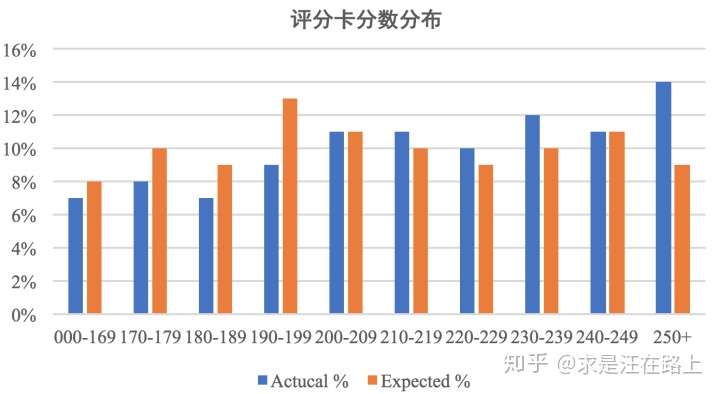图 1 - 分数分布差异对比

PSI的计算公式也告诉我们，的确是这样的：

PSI = SUM( (实际占比 - 预期占比）* ln(实际占比 / 预期占比) )

大多数同学到了这里，遵循拿来主义，直接应用。但是，大家有没有思考过以下几个问题：

Q1: 为什么要在计算公式中引入对数—— ln(实际占比 / 预期占比)？

Q2: 为什么log的底数是自然常数e，而不是其他常数（比如2）？（信息论中基常常选择为2，因此信息的单位为比特bits；而机器学习中基常选择为自然常数，因此单位常被称为奈特nats）

Q3: 如果只是衡量两个分布的差异，为什么不直接定义成以下公式呢？这个公式含义是把各个分数段里的人群占比差异进行累加放大。

自定义的稳定性指标 = SUM(实际占比 - 预期占比）

让我们先保留这些疑问，回到PSI的计算公式，以图2表格数据为例介绍下计算步骤。

• step1：将变量预期分布（excepted）进行分箱（binning）离散化，统计各个分箱里的样本占比。
  注意：
  a) 分箱可以是等频、等距或其他方式，分箱方式不同，将导致计算结果略微有差异；
  b) 对于连续型变量（特征变量、模型分数等），分箱数需要设置合理，一般设为10或20；对于离散型变量，如果分箱太多可以提前考虑合并小分箱；分箱数太多，可能会导致每个分箱内的样本量太少而失去统计意义；分箱数太少，又会导致计算结果精度降低。
• step2: 按相同分箱区间，对实际分布（actual）统计各分箱内的样本占比。
• step3:计 算各分箱内的A - E和Ln(A / E)，计算index = (实际占比 - 预期占比）* ln(实际占比 / 预期占比) 。
• step4: 将各分箱的index进行求和，即得到最终的PSI。

图 2 - PSI计算表格

在计算得到PSI指标后，这个数字又代表什么业务含义呢？PSI数值越小，两个分布之间的差异就越小，代表越稳定。

图 3 - PSI数值的业务含义

Part 3. 相对熵（KL散度）的理解

相对熵（relative entropy），又被称为Kullback-Leibler散度（Kullback-Leibler divergence）或信息散度（information divergence），是两个概率分布间差异的非对称性度量。

划重点——KL散度不满足对称性。

我们先不考虑相对熵的计算逻辑，先看它的物理含义是什么？

相对熵可以衡量两个随机分布之间的"距离“。
1）当两个随机分布相同时，它们的相对熵为零；当两个随机分布的差别增大时，它们的相对熵也会增大。
2）注意⚠️：相对熵是一个从信息论角度量化距离的指标，与数学概念上的距离有所差异。数学上的距离需要满足：非负性、对称性、同一性、传递性等；而相对熵不满足对称性。

看到这里，是不是感觉和PSI的概念非常相似？

当两个随机分布完全一样时，PSI = 0；反之，差异越大，PSI越大。

直觉告诉我们相对熵和PSI应该存在着某种隐含的关系，真相正在慢慢浮出水面。

我们再来看相对熵的计算公式。在信息理论中，相对熵等价于两个概率分布的信息熵（Shannon entropy）的差值。

其中，P(x)表示数据的真实分布，而Q(x)表示数据的观察分布。上式可以理解为：

概率分布携带着信息，可以用信息熵来衡量。
若用观察分布Q(x)来描述真实分布P(x)，还需要多少额外的信息量？

图 4 - KL散度具有非对称性

因此，KL散度是单向描述信息熵差异。为了加强大家理解，接下来以数值案例介绍相对熵如何计算。

假如一个字符发射器，随机发出0和1两种字符，真实发出概率分布为A，但实际不知道A的具体分布。通过观察，得到概率分布B与C，各个分布的具体情况如下：

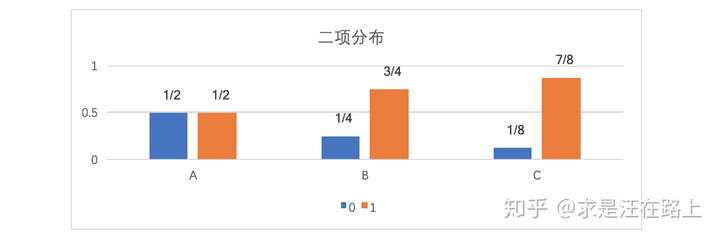图 5 - 三种数据分布

可以计算出得到KL散度如下：

由上式可知，相对熵KL(A||C) > KL(A||B)，说明A和B之间的概率分布在信息量角度更为接近。而通过概率分布可视化观察，我们也认为A和B更为接近，两者吻合。

Part 4. 相对熵与PSI之间的关系

接下来，我们从数学上来分析相对熵和PSI之间的关系。

将PSI计算公式变形后可以分解为2项，其中：

第1项：实际分布（A）与预期分布（E）之间的KL散度—— 
第2项：预期分布（E）与实际分布（A）之间的KL散度—— 

因此，PSI本质上是实际分布（A）与预期分布（E）的KL散度的一个对称化操作。其双向计算相对熵，并把两部分相对熵相加，从而更为全面地描述两个分布的差异。

至此，已经回答了上文的问题Q1——为什么要在计算公式中引入对数？

可能有人还会问，那为什么不把PSI定义成下式呢？

按笔者理解，一是为了保证数学公式的优雅；二是只要在同一尺度上比较，同时放大2倍也无所谓。

再回到上文的问题Q2——为什么log的底数是自然常数e，而不是其他常数（比如2）？按笔者理解，两者都可以，从信息量角度而言，底数为2或许更为合理。

至于问题Q3——为什么不定义为“SUM(实际占比 - 预期占比）”？这是因为有正有负，会存在相互抵消的现象。另一方面，也确实没有从相对熵角度来定义更为合理。

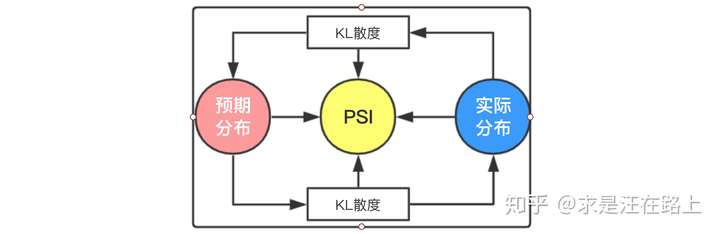图 6 - PSI与KL散度之间的关系

Part 5. PSI指标的业务应用

我们在业务上一般怎么用呢？一般以训练集（INS）的样本分布作为预期分布，进而跨时间窗按月/周来计算PSI，得到如图6所示的Monthly PSI Report，进而剔除不稳定的变量。同理，在模型上线部署后，也将通过PSI曲线报表来观察模型的稳定性。

入模变量保证稳定性，变量监控
模型分数保证稳定性，模型监控

根据建模经验，给出一些建议：

1. 实际评估需要分不同粒度：时间粒度（按月、按样本集）、订单层次（放贷层、申请层）、人群（若没有分群建模，可忽略）。

2. 先在放贷样本上计算PSI，剔除不稳定的特征；再对申请样本抽样（可能数据太大），计算PSI再次筛选。之前犯的错误就是只在放贷样本上评估，后来在全量申请订单上评估时发现并不稳定，导致返工。

3. 时间窗尽可能至今为止，有可能建模时间窗稳定，但近期时间窗出现不稳定。

4. PSI只是一个宏观的指标，建议先看变量数据分布（EDD），看分位数跨时间变化来检验数据质量。我们无法得知PSI上升时，数据分布是左偏还是右偏。因此，建议把PSI计算细节也予以保留，便于在模型不稳定时，第一时间排查问题。

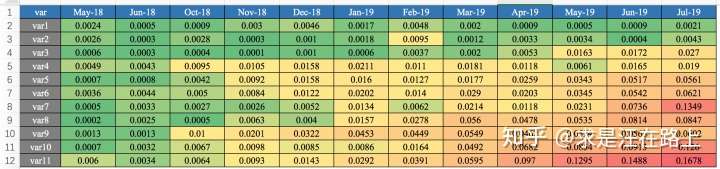图 7 - Monthly PSI Report

Part 6. PSI的计算代码（Python）

参考：https://github.com/mwburke/population-stability-index/blob/master/psi.py

def psi_for_continue_var(expected_array, actual_array, bins=10, bucket_type='bins', detail=False, save_file_path=None):
    '''
    ----------------------------------------------------------------------
    功能: 计算连续型变量的群体性稳定性指标（population stability index ,PSI）
    ----------------------------------------------------------------------
    :param expected_array: numpy array of original values，基准组
    :param actual_array: numpy array of new values, same size as expected，比较组
    :param bins: number of percentile ranges to bucket the values into，分箱数, 默认为10
    :param bucket_type: string, 分箱模式，'bins'为等距均分，'quantiles'为按等频分箱
    :param detail: bool, 取值为True时输出psi计算的完整表格, 否则只输出最终的psi值
    :param save_file_path: string, csv文件保存路径. 默认值=None. 只有当detail=Ture时才生效.
    ----------------------------------------------------------------------
    :return psi_value: 
            当detail=False时, 类型float, 输出最终psi计算值;
            当detail=True时, 类型pd.DataFrame, 输出psi计算的完整表格。最终psi计算值 = list(psi_value['psi'])[-1]
    ----------------------------------------------------------------------
    示例：
    >>> psi_for_continue_var(expected_array=df['score'][:400],
                             actual_array=df['score'][401:], 
                             bins=5, bucket_type='bins', detail=0)
    >>> 0.0059132756739701245
    ------------
    >>> psi_for_continue_var(expected_array=df['score'][:400],
                             actual_array=df['score'][401:], 
                             bins=5, bucket_type='bins', detail=1)
    >>>
    	score_range	expecteds	expected(%)	actucalsactucal(%)ac - ex(%)ln(ac/ex)psi	max
    0	[0.021,0.2095]	120.0	30.00	152.0	31.02	1.02	0.033434	0.000341	
    1	(0.2095,0.398]	117.0	29.25	140.0	28.57	-0.68	-0.023522	0.000159	
    2	(0.398,0.5865]	81.0	20.25	94.0	19.18	-1.07	-0.054284	0.000577	<<<<<<<
    3	(0.5865,0.7751]	44.0	11.00	55.0	11.22	0.22	0.019801	0.000045	
    4	(0.7751,0.9636]	38.0	9.50	48.0	9.80	0.30	0.031087	0.000091	
    5	>>> summary	400.0	100.00	489.0	100.00	NaN	NaN	0.001214	<<< result
    ----------------------------------------------------------------------
    知识:
    公式： psi = sum(（实际占比-预期占比）* ln(实际占比/预期占比))
    一般认为psi小于0.1时候变量稳定性很高，0.1-0.25一般，大于0.25变量稳定性差，建议重做。
    相对于变量分布(EDD)而言, psi是一个宏观指标, 无法解释两个分布不一致的原因。但可以通过观察每个分箱的sub_psi来判断。
    ----------------------------------------------------------------------
    '''
    import math
    import numpy as np
    import pandas as pd
    
    expected_array = pd.Series(expected_array).dropna()
    actual_array = pd.Series(actual_array).dropna()
    if isinstance(list(expected_array)[0], str) or isinstance(list(actual_array)[0], str):
        raise Exception("输入数据expected_array只能是数值型, 不能为string类型")
        
    """step1: 确定分箱间隔"""
    def scale_range(input_array, scaled_min, scaled_max):
        '''
        ----------------------------------------------------------------------
        功能: 对input_array线性放缩至[scaled_min, scaled_max]
        ----------------------------------------------------------------------
        :param input_array: numpy array of original values, 需放缩的原始数列
        :param scaled_min: float, 放缩后的最小值
        :param scaled_min: float, 放缩后的最大值
        ----------------------------------------------------------------------
        :return input_array: numpy array of original values, 放缩后的数列
        ----------------------------------------------------------------------
        '''
        input_array += -np.min(input_array) # 此时最小值放缩到0
        if scaled_max == scaled_min:
            raise Exception('放缩后的数列scaled_min = scaled_min, 值为{}, 请检查expected_array数值！'.format(scaled_max))
        scaled_slope = np.max(input_array) * 1.0 / (scaled_max - scaled_min)
        input_array /= scaled_slope
        input_array += scaled_min
        return input_array
    
    # 异常处理，所有取值都相同时, 说明该变量是常量, 返回999999
    if np.min(expected_array) == np.max(expected_array):
        return 999999
    
    breakpoints = np.arange(0, bins + 1) / (bins) * 100 # 等距分箱百分比
    if 'bins' == bucket_type:        # 等距分箱
        breakpoints = scale_range(breakpoints, np.min(expected_array), np.max(expected_array))
    elif 'quantiles' == bucket_type: # 等频分箱
        breakpoints = np.stack([np.percentile(expected_array, b) for b in breakpoints])
 
    """step2: 统计区间内样本占比"""
    def generate_counts(arr, breakpoints):
        '''
        ----------------------------------------------------------------------
        功能: Generates counts for each bucket by using the bucket values 
        ----------------------------------------------------------------------
        :param arr: ndarray of actual values
        :param breakpoints: list of bucket values
        ----------------------------------------------------------------------
        :return cnt_array: counts for elements in each bucket, length of breakpoints array minus one
        :return score_range_array: 分箱区间
        ----------------------------------------------------------------------
        '''
        def count_in_range(arr, low, high, start):
            '''
            ----------------------------------------------------------------------
            功能: 统计给定区间内的样本数(Counts elements in array between low and high values)
            ----------------------------------------------------------------------
            :param arr: ndarray of actual values
            :param low: float, 左边界
            :param high: float, 右边界
            :param start: bool, 取值为Ture时，区间闭合方式[low, high],否则为(low, high]
            ----------------------------------------------------------------------
            :return cnt_in_range: int, 给定区间内的样本数
            ----------------------------------------------------------------------
            '''
            if start:
                cnt_in_range = len(np.where(np.logical_and(arr >= low, arr <= high))[0])
            else:
                cnt_in_range = len(np.where(np.logical_and(arr > low, arr <= high))[0])
            return cnt_in_range
 
        cnt_array = np.zeros(len(breakpoints) - 1)
        score_range_array = [''] * (len(breakpoints) - 1)
        for i in range(1, len(breakpoints)):
            cnt_array[i-1] = count_in_range(arr, breakpoints[i-1], breakpoints[i], i==1)
            if 1 == i:
                score_range_array[i-1] = '[' + str(round(breakpoints[i-1], 4)) + ',' + str(round(breakpoints[i], 4)) + ']'
            else:   
                score_range_array[i-1] = '(' + str(round(breakpoints[i-1], 4)) + ',' + str(round(breakpoints[i], 4)) + ']'
                                                                                
        return (cnt_array, score_range_array)
 
    expected_cnt = generate_counts(expected_array, breakpoints)[0]
    expected_percents = expected_cnt / len(expected_array)
    actual_cnt = generate_counts(actual_array, breakpoints)[0]
    actual_percents = actual_cnt / len(actual_array)
    delta_percents = actual_percents - expected_percents
    score_range_array = generate_counts(expected_array, breakpoints)[1]
                                                                               
    """step3: 区间放缩"""
    def sub_psi(e_perc, a_perc):
        '''
        ----------------------------------------------------------------------
        功能: 计算单个分箱内的psi值。Calculate the actual PSI value from comparing the values.
             Update the actual value to a very small number if equal to zero
        ----------------------------------------------------------------------
        :param e_perc: float, 期望占比
        :param a_perc: float, 实际占比
        ----------------------------------------------------------------------
        :return value: float, 单个分箱内的psi值
        ----------------------------------------------------------------------
        '''
        if a_perc == 0: # 实际占比
            a_perc = 0.001
        if e_perc == 0: # 期望占比
            e_perc = 0.001
        value = (e_perc - a_perc) * np.log(e_perc * 1.0 / a_perc)
        return value
    
    """step4: 得到最终稳定性指标"""
    sub_psi_array = [sub_psi(expected_percents[i], actual_percents[i]) for i in range(0, len(expected_percents))]
    if detail:
        psi_value = pd.DataFrame()
        psi_value['score_range'] = score_range_array
        psi_value['expecteds'] = expected_cnt
        psi_value['expected(%)'] = expected_percents * 100
        psi_value['actucals'] = actual_cnt
        psi_value['actucal(%)'] = actual_percents * 100
        psi_value['ac - ex(%)'] = delta_percents * 100
        psi_value['actucal(%)'] = psi_value['actucal(%)'].apply(lambda x: round(x, 2))
        psi_value['ac - ex(%)'] = psi_value['ac - ex(%)'].apply(lambda x: round(x, 2))
        psi_value['ln(ac/ex)'] = psi_value.apply(lambda row: np.log((row['actucal(%)'] + 0.001) 
                                                                  / (row['expected(%)'] + 0.001)), axis=1)
        psi_value['psi'] = sub_psi_array
        flag = lambda x: '<<<<<<<' if x == psi_value.psi.max() else ''
        psi_value['max'] = psi_value.psi.apply(flag)
        psi_value = psi_value.append([{'score_range':'>>> summary', 
                                       'expecteds': sum(expected_cnt),
                                       'expected(%)':100, 
                                       'actucals': sum(actual_cnt),
                                       'actucal(%)':100, 
                                       'ac - ex(%)': np.nan,
                                       'ln(ac/ex)': np.nan,
                                       'psi': np.sum(sub_psi_array),
                                       'max':'<<< result'}], ignore_index=True)
        if save_file_path:
            if not isinstance(save_file_path, str):
                raise Exception('参数save_file_path类型必须是str, 同时注意csv文件后缀!')
            elif not save_file_path.endswith('.csv'):
                raise Exception('参数save_file_path不是csv文件后缀，请检查!')
            psi_value.to_csv(save_file_path, encoding='utf-8', index=1)
    else:
        psi_value = np.sum(sub_psi_array)
 
    return psi_value