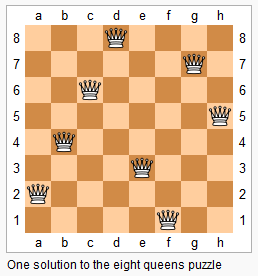
n皇后问题是一个以国际象棋为背景的问题:在n×n的国际象棋棋盘上放置n个皇后,使得任何一个皇后都无法直接吃掉其他的皇后,即任意两个皇后都不能处于同一条横行、纵行或斜线上。请问有多少种摆法,并将每种摆法打印出来。
递归算法1(最暴力的解法)
可以从左到右尝试棋子的摆放,例如先放置在第一行(1,1)放置,然后在第二行开始找与第一行放置不冲突的棋子,找到了(2,3),接着开始在第三行找,找到了(3,2)……一直到最后一行。如果出现下一行的每一列都有冲突,则返回到上一行,修改上一行的放置……重复上面的操作。
- 关于存储放置的棋子的坐标,一般会想到二维数组来存放,如arr[i][j]=1,代表i行,j列有棋子,实际上用一个一维数组就可以解决该问题。例如a[4]=1表示第4列有棋子,而且无需再判断两个皇后是否在同一行。
- 关于如何判断两个棋子在不在对角线,若两个棋子坐标(X 1,Y1),(X 2,Y2),则 |X 1-X2| != |Y 1-Y2|。当然在在之前应该首先判断在不在同一列(a[j]==y)
#include <iostream>
#include<cmath>
using namespace std;
int n,number;
int a[20]= {0};
int Try(int x,int y)/*测试x行y列可否摆放棋子*/
{
int j=1;
while(j<x) /*与数组中已放好的数比较*/
{
if((a[j]==y)||(abs(x-j)==abs(a[j]-y)))
return 0;
j++;
}
return 1;
}
void place(int x)//递归,x代表放置第几个棋子
{
if(x>n)
number++;//print();/*已到末尾结束,打印结果*/
else
{
for(int y=1; y<=n; y++) /*控制每一列的棋子进行尝试*/
{
if(Try(x,y))//如果可以摆放
{
a[x]=y;//在a中标记一下
place(x+1);/*继续下一列的递归*/
}
}
}
}
int main()
{
cin>>n;
place(1);
cout<<number<<endl;
}