1.poj 1330
数据结构中的树,在计算机科学中是非常重要的,例如我们来看看下面这棵树:
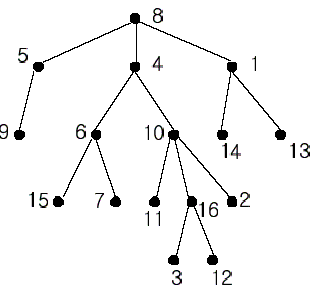
在图中我们对每个节点都有编号了。 8号节点是这棵树的根。我们定义,一个子节点向它的根节点的路径上,任意一个节点都称为它的祖先。例如, 4号节点是16号节点的祖先。而10号节点同样也是16号的祖先。事实上,16号的祖先有8,4,10,16共四个。另外8, 4, 6,7都是7号节点的祖先,所以7号和16号的公共祖先是4和8号,而在这两个里面,4号是距离7和16最近的一个,所以我们称7号和16号的最近公共祖先是4号。
再例如,2和3的最近公共祖先是10,再例如6和13的是8。
现在你需要编写一个程序,在一棵树中找出指定两个节点的最近公共祖先
Input
第一行输入T表示有T组数据。每组第一行是N表示这棵树有多少个节点,其中 2<=N<=10,000。 节点用正整数1, 2,..., N表示。 接下来的 N -1 行表示这棵树的边,每行两个数,都是节点编号,前一个是后一个的父节点。最后一行是要查询的两个节点,计算出这两个节点的最近公共祖先
Output
对于每组测试输出一行,输出它们的最近公共祖先的编号。
分析:lca
代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
using namespace std;
#define maxn 10005
int n,m,s;
int cnt,head[maxn],depth[maxn],p[maxn][25],fat[500005];
struct node{
int nxt,to;
}e[maxn];
void add(int x,int y){
e[++cnt].nxt=head[x];
head[x]=cnt;
e[cnt].to=y;
fat[y]=x;
}
void pre(int u,int fa){
depth[u]=depth[fa]+1;
p[u][0]=fa;
for(int i=1;1<<i<=depth[u];i++)p[u][i]=p[p[u][i-1]][i-1];
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v!=fa)pre(v,u);
}
}
int lca(int a,int b){
if(depth[a]>depth[b])swap(a,b);
for(int i=20;i>=0;i--){
if(depth[a]<=depth[b]-(1<<i))b=p[b][i];
}
if(a==b)return a;
for(int i=20;i>=0;i--){
if(p[a][i]==p[b][i])continue;
else a=p[a][i],b=p[b][i];
}
return p[a][0];
}
int main(){
int t;scanf("%d",&t);
while(t--){
memset(head,0,sizeof(head));
memset(depth,0,sizeof(depth));
memset(p,0,sizeof(p));
memset(fat,0,sizeof(fat));
memset(e,0,sizeof(e));
cnt=0;
scanf("%d",&n);
for(int i=1;i<n;i++){
int x,y;scanf("%d%d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;i++){
if(!fat[i]){
s=i;
break;
}
}
pre(s,0);
int a,b;scanf("%d%d",&a,&b);
printf("%d
",lca(a,b));
}
return 0;
}
T3 P4281
题目描述
欢乐岛上有个非常好玩的游戏,叫做“紧急集合”。在岛上分散有 nnn 个等待点,有 n−1n-1n−1 条道路连接着它们,每一条道路都连接某两个等待点,且通过这些道路可以走遍所有的等待点,通过道路从一个点到另一个点要花费一个游戏币。
参加游戏的人三人一组,开始的时候,所有人员均任意分散在各个等待点上(每个点同时允许多个人等待),每个人均带有足够多的游戏币(用于支付使用道路的花费)、地图(标明等待点之间道路连接的情况)以及对话机(用于和同组的成员联系)。当集合号吹响后,每组成员之间迅速联系,了解到自己组所有成员所在的等待点后,迅速在 nnn 个等待点中确定一个集结点,组内所有成员将在该集合点集合,集合所用花费最少的组将是游戏的赢家。
小可可和他的朋友邀请你一起参加这个游戏,由你来选择集合点,聪明的你能够完成这个任务,帮助小可可赢得游戏吗?
输入格式
第一行两个正整数 nnn 和 mmm,分别表示等待点的个数(等待点也从 111 到 nnn 进行编号)和获奖所需要完成集合的次数。随后 n−1n-1n−1 行,每行两个正整数 a,ba,ba,b,表示编号为 aaa 和编号为 bbb 的等待点之间有一条路。随后 mmm 行,每行用三个正整数 x,y,zx,y,zx,y,z,表示某次集合前小可可、小可可的朋友以及你所在等待点的编号。
输出格式
输出共 mmm 行,每行两个用空格隔开的整数 p,cp,cp,c。其中第 iii 行表示第 iii 次集合点选择在编号为 ppp 的等待点,集合总共的花费是 ccc 个游戏币。
分析:
经分析,对每两个点求lca,三个点一定有其中两个lca相同,并在另一个lca上面,下面的lca一定是到三点路径并最小的,正确性显然。
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
#define maxn 500005
int n,m,s;
int cnt,head[maxn],depth[maxn],p[maxn][25],fat[maxn];
struct node{
int nxt,to;
}e[2*maxn];
void add(int x,int y){
e[++cnt].nxt=head[x];
head[x]=cnt;
e[cnt].to=y;
}
void pre(int u,int fa){
depth[u]=depth[fa]+1;
fat[u]=fa;
p[u][0]=fa;
for(int i=1;1<<i<=depth[u];i++)p[u][i]=p[p[u][i-1]][i-1];
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v!=fa)pre(v,u);
}
}
int lca(int a,int b){
if(depth[a]>depth[b])swap(a,b);
for(int i=20;i>=0;i--){
if(depth[a]<=depth[p[b][i]])b=p[b][i];//printf("$$$$%d %d
",i,b);
}
//printf("%d %d
",a,b);
if(a==b)return a;
for(int i=20;i>=0;i--){
if(p[a][i]==p[b][i])continue;
else a=p[a][i],b=p[b][i];
}
return p[a][0];
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++){
int a,b;scanf("%d%d",&a,&b);
add(a,b);add(b,a);
}
pre(1,0);
//printf("sidjhsdl%d
",depth[0]);
//for(int i=1;i<=n;i++){
// printf("%d",depth[i]);
// }
for(int i=1;i<=m;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
int aa=lca(x,y);
int bb=lca(x,z);
int cc=lca(y,z);
// printf("%d %d %d
",aa,bb,cc);
int t;
if(aa==bb)t=cc;
if(aa==cc)t=bb;
if(bb==cc)t=aa;
printf("%d %d
",t,depth[x]+depth[y]+depth[z]-depth[aa]-depth[bb]-depth[cc]);
}
return 0;
}