洛谷 P1330 封锁阳光大学题解

题目描述

曹是一只爱刷街的老曹，暑假期间，他每天都欢快地在阳光大学的校园里刷街。河蟹看到欢快的曹，感到不爽。河蟹决定封锁阳光大学，不让曹刷街。

阳光大学的校园是一张由N个点构成的无向图，N个点之间由M条道路连接。每只河蟹可以对一个点进行封锁，当某个点被封锁后，与这个点相连的道路就被封锁了，曹就无法在与这些道路上刷街了。非常悲剧的一点是，河蟹是一种不和谐的生物，当两只河蟹封锁了相邻的两个点时，他们会发生冲突。

询问：最少需要多少只河蟹，可以封锁所有道路并且不发生冲突。

输入格式

第一行：两个整数N，M

接下来M行：每行两个整数A，B，表示点A到点B之间有道路相连。

输出格式

仅一行：如果河蟹无法封锁所有道路，则输出“Impossible”，否则输出一个整数，表示最少需要多少只河蟹。

输入输出样例

输入 #1复制

3 3
1 2
1 3
2 3

输出 #1复制

Impossible

输入 #2复制

3 2
1 2
2 3

输出 #2复制

1

说明/提示

【数据规模】

1<=N<=10000，1<=M<=100000，任意两点之间最多有一条道路。

---

题解

本题实际上是一道二分图的题目。

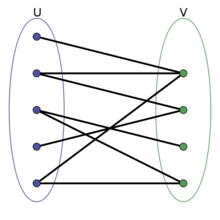
如果我们把图中U、V两个集合中的所有连线都用河蟹断开，就达到了题目要求。要判断图中的二分图，只需要类似01迷宫进行BFS遍历染色即可。在染色的过程中，如果发现连线的另一个端点未染色，就用和当前端点不同的颜色染色，要是已经染色且和当前节点颜色相同，就说明构成循环圈，不能构成二分图，类似下图的情况。

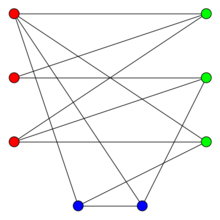
代码如下：

#include <iostream>
#include <math.h>
#include <stdio.h>
#include <algorithm>
#include <string.h>

using namespace std;

const int MAXN = 100005;
int first[MAXN], n, m, en, color[MAXN], f[2], u, v; //f统计不同颜色节点数 
int front, rear; 
bool vis[MAXN]; 
int ans;

struct edge
{
    int zhongdian, changdu;
    int next;
};

edge ed[MAXN]; 

void add_edge(int s, int e, int d) 
{
    en++; 
    ed[en].next = first[s]; 
    first[s] = en;
    ed[en].zhongdian = e;
    ed[en].changdu = d;
}

struct Node
{
    int x, y;
    int step;
};
Node q[MAXN];

int bfs(int a)
{
    Node now, next;
    now.x = a;
    vis[a] = 1;
    color[a] = 1;
    f[0] = 0;
    f[1] = 1;
    front = rear = 0;
    q[rear] = now;
    rear++;
    while(front < rear)
    {
        now = q[front++];
        for(int i = first[now.x]; i; i = ed[i].next)
        //first[now]：当前点的第一条边；ed[i].next：下一个访问的点  
        {
            if(color[ed[i].zhongdian] != -1)
            {
                if(color[ed[i].zhongdian] == color[now.x])
                {
                    cout << "Impossible" << endl;
                    return -1;
                }
            } 
            else
            {
                color[ed[i].zhongdian] = (color[now.x] + 1) % 2;
                q[rear].x = ed[i].zhongdian;
                rear++;
                f[color[ed[i].zhongdian]]++;
            }
        } 
    }
    ans += min(f[0], f[1]);
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        color[i] = -1; //初始化  
    }
    for(int i = 1; i <= m; i++)
    {
        cin >> u >> v;
        add_edge(u, v, 0);
        add_edge(v, u, 0);
    }
    for(int i = 1; i <= n; i++)
    {
        if(color[i] == -1)
        {
            if(bfs(i) < 0)
            {
                return 0;
            }
        } 
    }
    cout << ans << endl;
    
    return 0;
}

代码中的f数组是用来统计黑白两种染色点的个数的，本题所求的最小河蟹数就是两种染色点个数的最小值。