题意:将 $2n$ 个点两两匹配为 $n$ 个点对,问有多少方案满足:
- 任意两个点对,至少满足【距离相等】或【一对点 在 另一对点连接成的线段上】的其中一个条件。
答案对 $998244353$ 取模,$n le 10^6$。
解析
看 $n le 10^6$ 就应该知道这不是结论题,OEIS 大概率找不到。
我们尝试分类点对分布的情况,如下图是 $n=3$ 的所有方案。
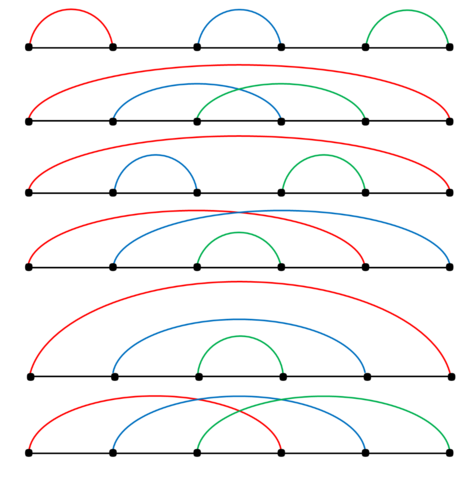
显然,我们可以进行第一次分类:当 $1,2n$ 两点匹配,中间会留下 $2n-2$ 个点(上图第 $2,3,5$ 个例子),因此 $n$ 的方案数一定被 $n-1$ 的方案数影响。
同理,当 $1,2n-1$ 与 $2,2n$ 都匹配时,中间会留下 $2n-4$ 个点(上图第 $4$ 个例子),因此 $n$ 的方案数还被 $n-2$ 的方案数影响。
结论一:$n$ 的方案数与 $0~(n-1)$ 的方案数的和有关。
那么数到这,上图的第 $1,6$ 个例子还没有提及,我们可以试着讨论一下。
但看了半天,除了第 $1$ 个例子被分成 $3$ 段,第 $6$ 个例子还是 $1$ 段以外没有别的什么特点。
这时不妨画一画 $n=4$ 的情况(其余 $10$ 种最外面有环的方案省略):
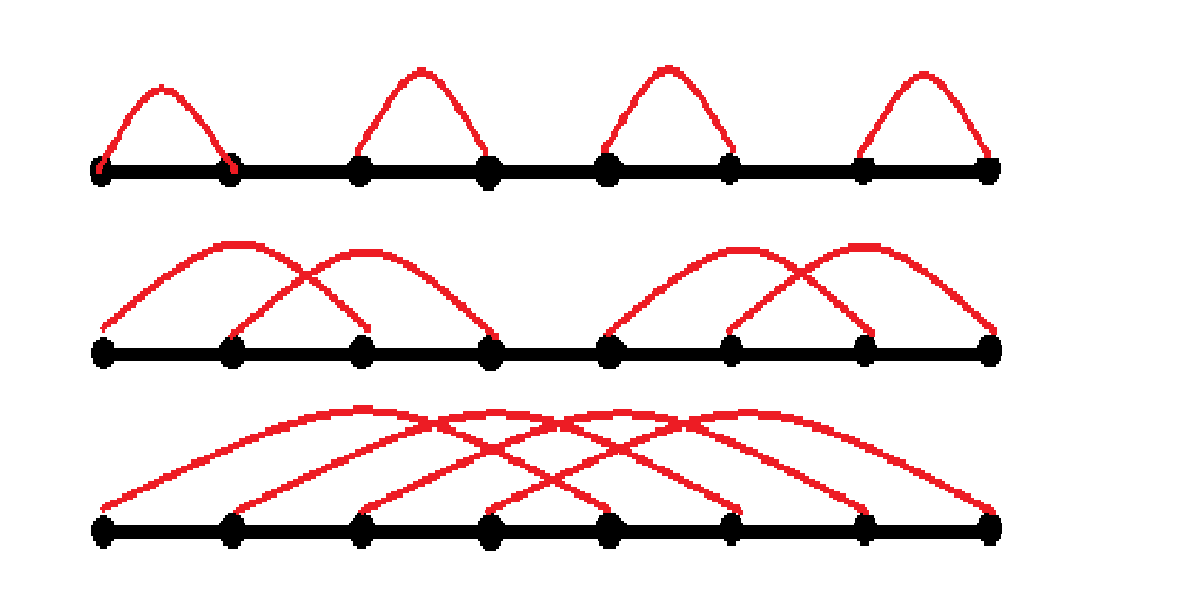
可以发现,如果要将 $2n$ 个点分为若干个互不相交的段,分的段数必须是 $n$ 的因数。
而每种因数分别代表一种情况。
所以,设 $2n$ 个点的方案数为 $dp_n$,那么有方程式($d(i)$ 指 $i$ 的约数个数)
$$dp_i=d(i)+sum_{j=0}^{i-1}dp_j$$
$1 sim n$ 的 $d(i)$ 可以用类似埃拉托色尼筛法的办法以 $O(n log n)$ 的复杂度解决,而 $sum dp_j$ 可以递推解决。
代码
#include <cstdio> #define INF 1e9 #define eps 1e-6 #define MOD 998244353 typedef long long ll; int n, s[1000010], dp[1000010], sum, ans; int main(){ scanf("%d", &n); for(int i = 1; i <= n; i++) for(int j = i; j <= n; j += i) s[j]++; for(int i = 1; i <= n; i++){ dp[i] = (sum + s[i]) % MOD; sum = (sum + dp[i]) % MOD; } printf("%d ", dp[n]); return 0; }