Codeforces Round #292 (Div. 2)——C——Drazil and Factorial

Drazil is playing a math game with Varda.

Let's define 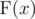 for positive integer x as a product of factorials of its digits. For example, .

First, they choose a decimal number a consisting of n digits that contains at least one digit larger than 1. This number may possibly start with leading zeroes. Then they should find maximum positive number x satisfying following two conditions:

1. x doesn't contain neither digit 0 nor digit 1.

2.  = .

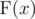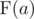Help friends find such number.

Input

The first line contains an integer n (1 ≤ n ≤ 15) — the number of digits in a.

The second line contains n digits of a. There is at least one digit in a that is larger than 1. Number a may possibly contain leading zeroes.

Output

Output a maximum possible integer satisfying the conditions above. There should be no zeroes and ones in this number decimal representation.

Sample test(s)

input

4
1234

output

33222

input

3
555

output

555

Note

In the first case, 

大意：让你算出阶乘相同的序列最大的数是多少，即能分成的最多的数，再把他们从大到小排列，把1到9所有数能分的都写出来然后用一个数组b记录。

思路比较简单

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
int main()
{
    int n;
   char a[20];
   int  b[100];
    scanf("%d",&n);
    getchar();
        scanf("%s",a);
        int count = 0;
    for(int i = 0; i < n ; i++){
        switch(a[i]){
      case'2':b[count++] = 2;break;
      case'3':b[count++] = 3;break;
      case'4':b[count++] = 3;b[count++]=2;b[count++]=2;break;
      case'5':b[count++] = 5;break;
      case'6':b[count++] = 5;b[count++]=3;break;
      case'7':b[count++] = 7;break;
      case'8':b[count++] = 7;b[count++]=2;b[count++]=2;b[count++]=2;break;
      case'9':b[count++] = 7;b[count++]=3;b[count++]=3;b[count++]=2;break;
        }
    }
    count--;
    sort(b,b+count+1);
    for(int i = count;i >= 0;i--)
        printf("%d",b[i]);
   return 0;
}