LeetCode 258. Add Digits

Given a non-negative integer num, repeatedly add all its digits until the result has only one digit.

For example:

Given num = 38, the process is like: 3 + 8 = 11, 1 + 1 = 2. Since 2 has only one digit, return it.

Follow up:
Could you do it without any loop/recursion in O(1) runtime?

Credits:
Special thanks to @jianchao.li.fighter for adding this problem and creating all test cases.

题意：给定一个非负整数，将其每位上的数字加起来，重复此操作，直到相加的和为一位数
follow up：要求时间复杂度为O(1)，不使用循环或递归

方法一：直接计算。但要使用循环。时间复杂度高

public int addDigits(int num) {
        int sum = 0;
        while(num / 10 != 0){
            while(num % 10 != 0 || num != 0){
                sum += num % 10;
                num /= 10;
            }
            num = sum;
            sum = 0;
        }
        return num;
    }

方法二：参考：https://www.cnblogs.com/grandyang/p/4741028.html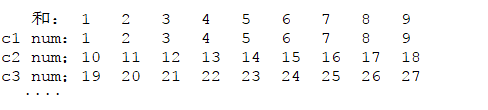

可看出：c3列每个数相加，变成对应的c2列；而c2列的每个数相加，又变成对应的c1列。
可得出规律：每9个数为一个循环，所求的sum为num除以9取余，即num % 9。但是存在一个问题，即像9、18、27这些除以9余数为0.
因此为了对所有数都适用，改为：(num - 1) % 9 + 1

public int addDigits(int num){
        return (num - 1) % 9 + 1;
    }