Arcface训练问题分析
1、现象
使用ArcFace 层时,训练前期准确率一直为0,到后面才逐渐上升;
2、分析
从代码入手
output = (y * phi) + ((1.0 - y) * cosine)
output *= s
y 是one-hot形式的真实label,phi=cos(θ+m),cosine=cosθ,θ即特征向量与权值向量的夹角。则:
(1) label = 0 -> y=[1, 0] -> output = [s*cos(θ1+m), s*cosθ2]
(2) label = 1 -> y=[0,1] -> output = [s*cosθ1, s*cos(θ2+m)]
然后经过softmax操作进行概率转换;
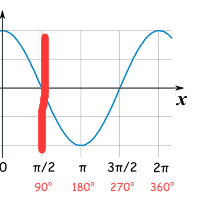
初始时,θ1和θ2在高维空间中均接近pi/2,m一般为正数(这里为0.05)。针对softmax的输出使用CE-loss进行约束,形式如下:
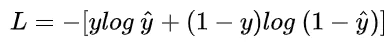
则:
(1) label = 0 -> 损失函数会朝着s*cos(θ1+m) >> s*cosθ2 的方向约束,结合cos函数在[0, pi]上的单调递减性,则(θ1+m) 应越来越小于 θ2;但是初始时 θ1=θ2=pi/2,则θ1+m 在训练初期都大于θ2,即训练初期 s*cos(θ1+m) < s*cosθ2 ,即label = 0 时, prediction =1;
(2) label = 1时的情况同上
所以训练初期:label = 0 的样本都被判为负样本,label = 1的样本都被判为正样本,所以训练初期acc = 0%。
而随着训练的不断进行,比如对于label = 0时, θ1从pi/2缩小到pi/2 -m 至更小时,则acc开始上升。
备注:m值需为正数,它代表着类别在角度空间中的margin。若m为负数,则根据上面的分析可知:训练初期就有θ1+m<θ2,从而导致对于θ1没有惩罚作用。(训练时acc均为100%)