NMS和soft-nms算法

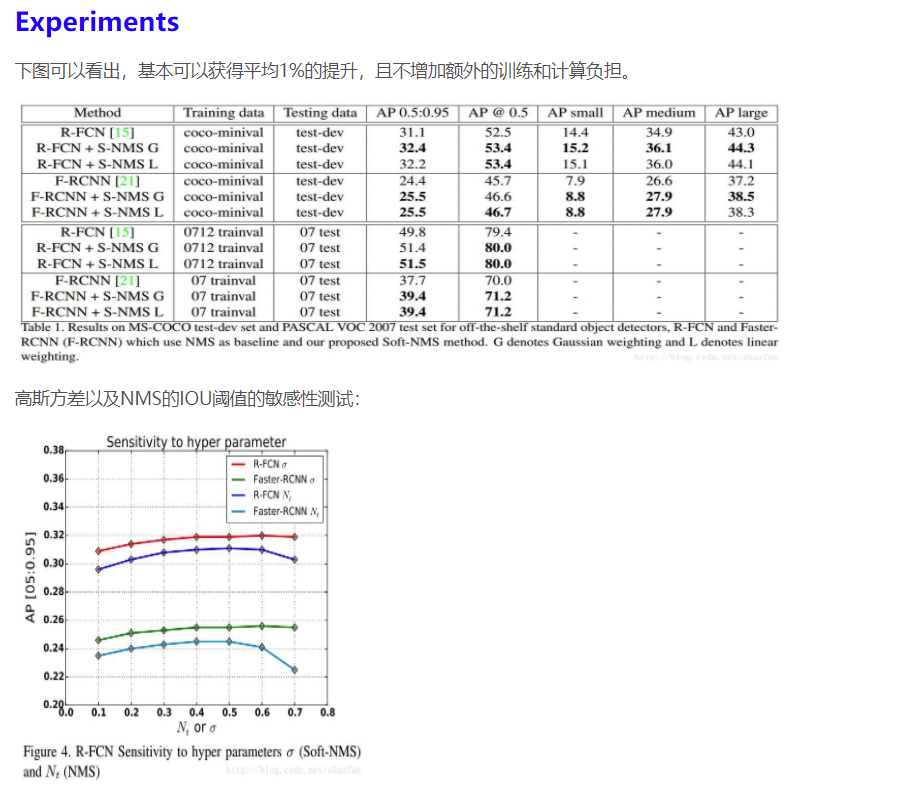
非极大值抑制算法(nms)

1. 算法原理

  非极大值抑制算法（Non-maximum suppression, NMS）的本质是搜索局部极大值，抑制非极大值元素。

2. 3邻域情况下NMS的实现

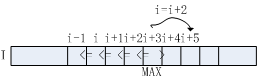
  3邻域情况下的NMS即判断一维数组I[W]的元素I[i](2<=i<=W-1)是否大于其左邻元素I[i-1]和右邻元素I[i+1]，算法流程如下图所示：

  

  a. 算法流程3-5行判断当前元素是否大于其左邻与右邻元素，如符合条件，该元素即为极大值点。对于极大值点I[i]，已知I[i]>I[i+1]，故无需对i+1位置元素做进一步处理，直接跳至i+2位置，对应算法流程第12行。

    

  b. 若元素I[i]不满足算法流程第3行判断条件，将其右邻I[i+1]作为极大值候选，对应算法流程第7行。采用单调递增的方式向右查找，直至找到满足I[i]>I[i+1]的元素，若i<=W-1，该点即为极大值点，对应算法流程第10-11行。

    

3. NMS在物体检测中的应用

  物体检测中应用NMS算法的主要目的是消除多余（交叉重复）的窗口，找到最佳物体检测位置。

  

  如上图所示，人脸检测中，虽然每个窗口均检测到人脸，但仅需给出一个最有可能表征人脸的窗口

程序整体思路：

         先将box中的数据分别存入x1，y1，x2，y2，s中，分别为坐标和置信度，算出每个框的面积，存入area，基于置信度s，从小到达进行排序，做一个while循环，取出置信度最高的，即排序后的最后一个，然后将该框进行保留，存入pick中，然后和其他所有的框进行比对，大于规定阈值就将别的框去掉，并将该置信度最高的框和所有比对过程，大于阈值的框存入suppress，for循环后，将I中满足suppress条件的置为空。直到I为空退出while。

代码（C++）：

static void sort(int n, const float* x, int* indices)  
{  
// 排序函数(降序排序)，排序后进行交换的是indices中的数据  
// n：排序总数// x：带排序数// indices：初始为0~n-1数目   
  
    int i, j;  
    for (i = 0; i < n; i++)  
        for (j = i + 1; j < n; j++)  
        {  
            if (x[indices[j]] > x[indices[i]])  
            {  
                //float x_tmp = x[i];  
                int index_tmp = indices[i];  
                //x[i] = x[j];  
                indices[i] = indices[j];  
                //x[j] = x_tmp;  
                indices[j] = index_tmp;  
            }  
        }  
}

int nonMaximumSuppression(int numBoxes, const CvPoint *points,  
                          const CvPoint *oppositePoints, const float *score,  
                          float overlapThreshold,  
                          int *numBoxesOut, CvPoint **pointsOut,  
                          CvPoint **oppositePointsOut, float **scoreOut)  
{  
  
// numBoxes：窗口数目// points：窗口左上角坐标点// oppositePoints：窗口右下角坐标点  
// score：窗口得分// overlapThreshold：重叠阈值控制// numBoxesOut：输出窗口数目  
// pointsOut：输出窗口左上角坐标点// oppositePoints：输出窗口右下角坐标点  
// scoreOut：输出窗口得分  
    int i, j, index;  
    float* box_area = (float*)malloc(numBoxes * sizeof(float));    // 定义窗口面积变量并分配空间   
    int* indices = (int*)malloc(numBoxes * sizeof(int));          // 定义窗口索引并分配空间   
    int* is_suppressed = (int*)malloc(numBoxes * sizeof(int));    // 定义是否抑制表标志并分配空间   
    // 初始化indices、is_supperssed、box_area信息   
    for (i = 0; i < numBoxes; i++)  
    {  
        indices[i] = i;  
        is_suppressed[i] = 0;  
        box_area[i] = (float)( (oppositePoints[i].x - points[i].x + 1) *  
                                (oppositePoints[i].y - points[i].y + 1));  
    }  
    // 对输入窗口按照分数比值进行排序，排序后的编号放在indices中   
    sort(numBoxes, score, indices);  
    for (i = 0; i < numBoxes; i++)                // 循环所有窗口   
    {  
        if (!is_suppressed[indices[i]])           // 判断窗口是否被抑制   
        {  
            for (j = i + 1; j < numBoxes; j++)    // 循环当前窗口之后的窗口   
            {  
                if (!is_suppressed[indices[j]])   // 判断窗口是否被抑制   
                {  
                    int x1max = max(points[indices[i]].x, points[indices[j]].x);                     // 求两个窗口左上角x坐标最大值   
                    int x2min = min(oppositePoints[indices[i]].x, oppositePoints[indices[j]].x);     // 求两个窗口右下角x坐标最小值   
                    int y1max = max(points[indices[i]].y, points[indices[j]].y);                     // 求两个窗口左上角y坐标最大值   
                    int y2min = min(oppositePoints[indices[i]].y, oppositePoints[indices[j]].y);     // 求两个窗口右下角y坐标最小值   
                    int overlapWidth = x2min - x1max + 1;            // 计算两矩形重叠的宽度   
                    int overlapHeight = y2min - y1max + 1;           // 计算两矩形重叠的高度   
                    if (overlapWidth > 0 && overlapHeight > 0)  
                    {  
                        float overlapPart = (overlapWidth * overlapHeight) / box_area[indices[j]];    // 计算重叠的比率   
                        if (overlapPart > overlapThreshold)          // 判断重叠比率是否超过重叠阈值   
                        {  
                            is_suppressed[indices[j]] = 1;           // 将窗口j标记为抑制   
                        }  
                    }  
                }  
            }  
        }  
    }  
  
    *numBoxesOut = 0;    // 初始化输出窗口数目0   
    for (i = 0; i < numBoxes; i++)  
    {  
        if (!is_suppressed[i]) (*numBoxesOut)++;    // 统计输出窗口数目   
    }  
  
    *pointsOut = (CvPoint *)malloc((*numBoxesOut) * sizeof(CvPoint));           // 分配输出窗口左上角坐标空间   
    *oppositePointsOut = (CvPoint *)malloc((*numBoxesOut) * sizeof(CvPoint));   // 分配输出窗口右下角坐标空间   
    *scoreOut = (float *)malloc((*numBoxesOut) * sizeof(float));                // 分配输出窗口得分空间   
    index = 0;  
    for (i = 0; i < numBoxes; i++)                  // 遍历所有输入窗口   
    {  
        if (!is_suppressed[indices[i]])             // 将未发生抑制的窗口信息保存到输出信息中   
        {  
            (*pointsOut)[index].x = points[indices[i]].x;  
            (*pointsOut)[index].y = points[indices[i]].y;  
            (*oppositePointsOut)[index].x = oppositePoints[indices[i]].x;  
            (*oppositePointsOut)[index].y = oppositePoints[indices[i]].y;  
            (*scoreOut)[index] = score[indices[i]];  
            index++;  
        }  
  
    }  
  
    free(indices);          // 释放indices空间   
    free(box_area);         // 释放box_area空间   
    free(is_suppressed);    // 释放is_suppressed空间   
  
    return LATENT_SVM_OK;  
}  

软化非极大值抑制算法（softnms）

参考链接：http://blog.csdn.net/app_12062011/article/details/77963494

Motivation

绝大部分目标检测方法，最后都要用到 NMS-非极大值抑制进行后处理。 通常的做法是将检测框按得分排序，然后保留得分最高的框，同时删除与该框重叠面积大于一定比例的其它框。

这种贪心式方法存在如下图所示的问题： 红色框和绿色框是当前的检测结果，二者的得分分别是0.95和0.80。如果按照传统的NMS进行处理，首先选中得分最高的红色框，然后绿色框就会因为与之重叠面积过大而被删掉。

另一方面，NMS的阈值也不太容易确定，设小了会出现下图的情况（绿色框因为和红色框重叠面积较大而被删掉），设置过高又容易增大误检。

思路：不要粗鲁地删除所有IOU大于阈值的框，而是降低其置信度。

Method

先直接上伪代码，如下图：如文章题目而言，就是用一行代码来替换掉原来的NMS。按照下图整个处理一遍之后，指定一个置信度阈值，然后最后得分大于该阈值的检测框得以保留

原来的NMS可以描述如下：将IOU大于阈值的窗口的得分全部置为0。

文章的改进有两种形式，一种是线性加权的：

一种是高斯加权的：

分析上面的两种改进形式，思想都是：M为当前得分最高框， 为待处理框， 和M的IOU越大， 的得分 就下降的越厉害。

具体地，下面是作者给出的代码：(当然不止一行T_T)

def cpu_soft_nms(np.ndarray[float, ndim=2] boxes, float sigma=0.5, float Nt=0.3, float threshold=0.001, unsigned int method=0):
    cdef unsigned int N = boxes.shape[0]
    cdef float iw, ih, box_area
    cdef float ua
    cdef int pos = 0
    cdef float maxscore = 0
    cdef int maxpos = 0
    cdef float x1,x2,y1,y2,tx1,tx2,ty1,ty2,ts,area,weight,ov

    for i in range(N):
        maxscore = boxes[i, 4]
        maxpos = i

        tx1 = boxes[i,0]
        ty1 = boxes[i,1]
        tx2 = boxes[i,2]
        ty2 = boxes[i,3]
        ts = boxes[i,4]

        pos = i + 1
    # get max box
        while pos < N:
            if maxscore < boxes[pos, 4]:
                maxscore = boxes[pos, 4]
                maxpos = pos
            pos = pos + 1

    # add max box as a detection 
        boxes[i,0] = boxes[maxpos,0]
        boxes[i,1] = boxes[maxpos,1]
        boxes[i,2] = boxes[maxpos,2]
        boxes[i,3] = boxes[maxpos,3]
        boxes[i,4] = boxes[maxpos,4]

    # swap ith box with position of max box
        boxes[maxpos,0] = tx1
        boxes[maxpos,1] = ty1
        boxes[maxpos,2] = tx2
        boxes[maxpos,3] = ty2
        boxes[maxpos,4] = ts

        tx1 = boxes[i,0]
        ty1 = boxes[i,1]
        tx2 = boxes[i,2]
        ty2 = boxes[i,3]
        ts = boxes[i,4]

        pos = i + 1
    # NMS iterations, note that N changes if detection boxes fall below threshold
        while pos < N:
            x1 = boxes[pos, 0]
            y1 = boxes[pos, 1]
            x2 = boxes[pos, 2]
            y2 = boxes[pos, 3]
            s = boxes[pos, 4]

            area = (x2 - x1 + 1) * (y2 - y1 + 1)
            iw = (min(tx2, x2) - max(tx1, x1) + 1)
            if iw > 0:
                ih = (min(ty2, y2) - max(ty1, y1) + 1)
                if ih > 0:
                    ua = float((tx2 - tx1 + 1) * (ty2 - ty1 + 1) + area - iw * ih)
                    ov = iw * ih / ua #iou between max box and detection box

                    if method == 1: # linear
                        if ov > Nt: 
                            weight = 1 - ov
                        else:
                            weight = 1
                    elif method == 2: # gaussian
                        weight = np.exp(-(ov * ov)/sigma)
                    else: # original NMS
                        if ov > Nt: 
                            weight = 0
                        else:
                            weight = 1

                    boxes[pos, 4] = weight*boxes[pos, 4]

            # if box score falls below threshold, discard the box by swapping with last box
            # update N
                    if boxes[pos, 4] < threshold:
                        boxes[pos,0] = boxes[N-1, 0]
                        boxes[pos,1] = boxes[N-1, 1]
                        boxes[pos,2] = boxes[N-1, 2]
                        boxes[pos,3] = boxes[N-1, 3]
                        boxes[pos,4] = boxes[N-1, 4]
                        N = N - 1
                        pos = pos - 1

            pos = pos + 1

    keep = [i for i in range(N)]
    return keep

 这么做的解释如下：

如上图：

假如还检测出了3号框，而我们的最终目标是检测出1号和2号框，并且剔除3号框，原始的nms只会检测出一个1号框并剔除2号框和3号框，而softnms算法可以对1、2、3号检测狂进行置信度排序，可以知道这三个框的置信度从大到小的顺序依次为：1-》2-》3（由于是使用了惩罚，所有可以获得这种大小关系），如果我们再选择了合适的置信度阈值，就可以保留1号和2号，同时剔除3号，实现我们的功能。

但是，这里也有一个问题就是置信度的阈值如何选择，作者在这里依然使用手工设置的值，依然存在很大的局限性，所以该算法依然存在改进的空间。

result: