参考链接:https://www.cnblogs.com/skywang12345/p/3576328.html
定义:二叉查找树(Binary Search Tree),又被称为二叉搜索树。设x为二叉查找树中的一个结点,x节点包含关键字key,节点x的key值记为key[x]。如果y是x的左子树中的一个结点,则key[y] <= key[x];如果y是x的右子树的一个结点,则key[y] >= key[x]。
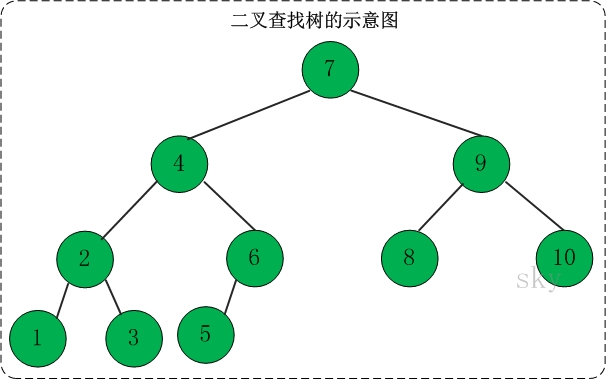
在二叉查找树中:
(01) 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(02) 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点(no duplicate nodes)。
代码如下:
1. 节点定义
1.1 节点定义
typedef int Type; typedef struct BSTreeNode{ Type key; // 关键字(键值) struct BSTreeNode *left; // 左孩子 struct BSTreeNode *right; // 右孩子 struct BSTreeNode *parent; // 父结点 }Node, *BSTree;
1.2 创建节点
创建节点的代码
static Node* create_bstree_node(Type key, Node *parent, Node *left, Node* right) { Node* p; if ((p = (Node *)malloc(sizeof(Node))) == NULL) return NULL; p->key = key; p->left = left; p->right = right; p->parent = parent; return p; }
2 遍历
2.1 前序遍历
void preorder_bstree(BSTree tree) { if(tree != NULL) { printf("%d ", tree->key); preorder_bstree(tree->left); preorder_bstree(tree->right); } }
2.2 中序遍历
void inorder_bstree(BSTree tree) { if(tree != NULL) { inorder_bstree(tree->left); printf("%d ", tree->key); inorder_bstree(tree->right); } }
2.3 后序遍历
void postorder_bstree(BSTree tree) { if(tree != NULL) { postorder_bstree(tree->left); postorder_bstree(tree->right); printf("%d ", tree->key); } }
3. 查找
递归版本的代码:
Node* bstree_search(BSTree x, Type key) { if (x==NULL || x->key==key) return x; if (key < x->key) return bstree_search(x->left, key); else return bstree_search(x->right, key); }
非递归版本的代码:
Node* iterative_bstree_search(BSTree x, Type key) { while ((x!=NULL) && (x->key!=key)) { if (key < x->key) x = x->left; else x = x->right; } return x; }
4. 最大值和最小值
查找最大值的代码:
Node* bstree_maximum(BSTree tree) { if (tree == NULL) return NULL; while(tree->right != NULL) tree = tree->right; return tree; }
查找最小值的代码
Node* bstree_minimum(BSTree tree) { if (tree == NULL) return NULL; while(tree->left != NULL) tree = tree->left; return tree; }
5. 前驱和后继:
什么是后继和前驱,如果对数的节点的关键字排序:
key1<=key2<=......<=keyn−3<=keyn−2<=keyn−1<=keynkey1<=key2<=......<=keyn−3<=keyn−2<=keyn−1<=keyn,那么keyn−3keyn−3和keyn−1keyn−1就是keyn−2keyn−2的前驱和后继;
查找前驱节点的代码:
Node* bstree_predecessor(Node *x) { // 如果x存在左孩子,则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。 if (x->left != NULL) return bstree_maximum(x->left); // 如果x没有左孩子。则x有以下两种可能: // (01) x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。 // (01) x是"一个左孩子",则查找"x的最低的父结点,并且该父结点要具有右孩子",找到的这个"最低的父结点"就是"x的前驱结点"。 Node* y = x->parent; while ((y!=NULL) && (x==y->left)) { x = y; y = y->parent; } return y; }
查找后继节点的代码:
Node* bstree_successor(Node *x) { // 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。 if (x->right != NULL) return bstree_minimum(x->right); // 如果x没有右孩子。则x有以下两种可能: // (01) x是"一个左孩子",则"x的后继结点"为 "它的父结点"。 // (02) x是"一个右孩子",则查找"x的最低的父结点,并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。 Node* y = x->parent; while ((y!=NULL) && (x==y->right)) { x = y; y = y->parent; } return y; }