Packmen CodeForces

A game field is a strip of 1 × n square cells. In some cells there are Packmen, in some cells — asterisks, other cells are empty.

Packman can move to neighboring cell in 1 time unit. If there is an asterisk in the target cell then Packman eats it. Packman doesn't spend any time to eat an asterisk.

In the initial moment of time all Packmen begin to move. Each Packman can change direction of its move unlimited number of times, but it is not allowed to go beyond the boundaries of the game field. Packmen do not interfere with the movement of other packmen; in one cell there can be any number of packmen moving in any directions.

Your task is to determine minimum possible time after which Packmen can eat all the asterisks.

Input

The first line contains a single integer n (2 ≤ n ≤ 10⁵) — the length of the game field.

The second line contains the description of the game field consisting of n symbols. If there is symbol '.' in position i — the cell i is empty. If there is symbol '*' in position i — in the cell i contains an asterisk. If there is symbol 'P' in position i — Packman is in the cell i.

It is guaranteed that on the game field there is at least one Packman and at least one asterisk.

Output

Print minimum possible time after which Packmen can eat all asterisks.

Example

Input

7
*..P*P*

Output

3

Input

10
.**PP.*P.*

Output

2

Note

In the first example Packman in position 4 will move to the left and will eat asterisk in position 1. He will spend 3 time units on it. During the same 3 time units Packman in position 6 will eat both of neighboring with it asterisks. For example, it can move to the left and eat asterisk in position 5 (in 1 time unit) and then move from the position 5 to the right and eat asterisk in the position 7 (in 2 time units). So in 3 time units Packmen will eat all asterisks on the game field.

In the second example Packman in the position 4 will move to the left and after 2 time units will eat asterisks in positions 3 and 2. Packmen in positions 5 and 8 will move to the right and in 2 time units will eat asterisks in positions 7 and 10, respectively. So 2 time units is enough for Packmen to eat all asterisks on the game field.

题解：二分时间，然后检查答案（emmmmm，然而check不会写），借鉴大佬的代码（》《）

官方：这是 codeforces 343c Read Time的题解，不过和这道题是相同的解法

Let's search the answer t with the binary search. Fix some value of t. Look at the first head from the left h[i] that can read track p[0]. If p[0] > h[i], then h[i] goes to the right t seconds and reads all tracks on its way. Otherwise if p[0] ≤ h[i], then the head has two choices:

1. go to the right 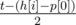seconds, then 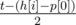to the left and h[i] - p[0] again to the left;
2. go to the left h[i] - p[0] seconds, then h[i] - p[0] to the right and t - 2·(h[i] - p[0]) again to the right.

Obviously, for h[i] it is more advantageous to visit the track positioned as much as possible to the right. So we choose by 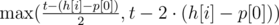. Then we move the pointer onto the first unread track, and repeat the algorithm for h[i + 1], and so on with each head.

Solution complexity: 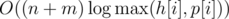. Problem authors

#include<bits/stdc++.h>
using namespace std;

const int maxn=1e5+5;

int n,pn,sn;
int p[maxn],x[maxn];
char S[maxn];

int calc(int l,int r,int pos){
    return min(abs(pos-l),abs(pos-r))+abs(r-l);
}

bool check(int temp){
    int pre=-1,pos=-1;
    for(int i=0;i<pn;i++){
        while((pos<sn-1)&&(calc(x[pre+1],x[pos+1],p[i])<=temp)) ++pos;
        pre=pos;
    }
    return pos==sn-1;
}

int main()
{   scanf("%d%s",&n,S);
    pn=0,sn=0;
    for(int i=0;i<n;i++){
        if(S[i]=='P') p[pn++]=i;
        if(S[i]=='*') x[sn++]=i;
    }
    int l=0,r=2*n;
    while(l<r){
        int mid=(l+r)>>1;
        if(check(mid)) r=mid;
        else l=mid+1;
    }
    printf("%d
",r);
}