Lucky Days -codeforce

题意

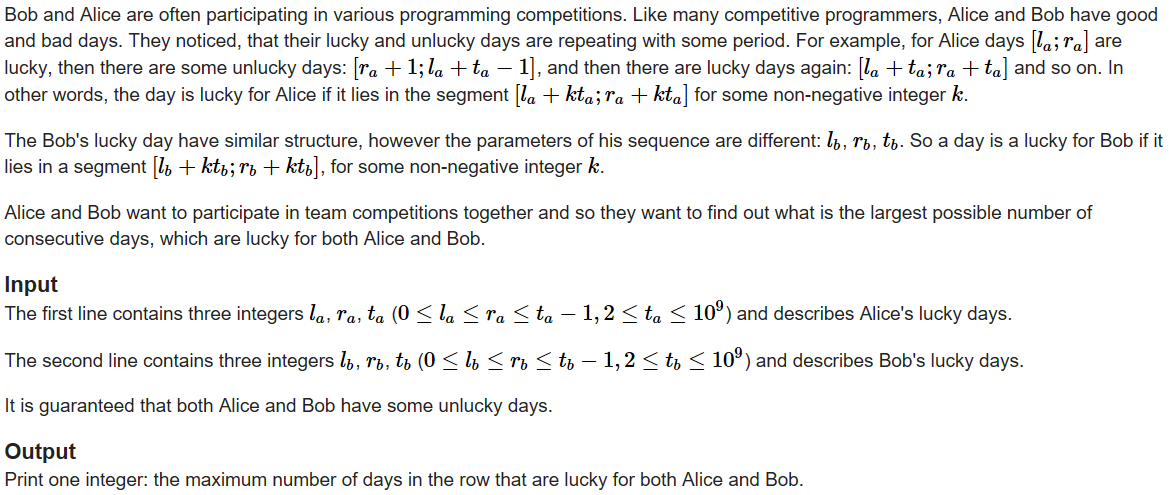
题解

线段([l_a + kt_a, r_a + kt_a])，([l_b + kt_b,r_b + kt_b ])相交，可以建立一个不等式：

[l_b leq y leq r_b ]

[y equiv l_a + kt_a (mod(t_b)) ]

转化一下：

[y = l_a + kt_a + ht_b ]

(k,h)都是变量，那么由欧几里得扩展可知：(k,h)存在时，(gcd(t_a,t_b) | (y - l_a))。至此，问题转化为在区间([l_b,r_b])，寻找一个(y)值使得(gcd(t_a,t_b)|(y - l_a))。如果是枚举区间内的数，复杂度会炸。稍微思考一下，不需要枚举整个区间的数，考察(y = l_b)和(y = y',frac{y' - l_a}{gcd(t_a,t_b)} = frac{l_b - l_a}{gcd(t_a,t_b)} + 1)。令(t = frac{l_b-l_a}{gcd(t_a,t_b)}​)，那么可以解得:

[y = t * gcd(t_a,t_b) + l_a ]

[y' = (t + 1) * gcd(t_a,t_b) + la ]

代码

#include <bits/stdc++.h>
using namespace std;

int la, ra, ta, lb, rb, tb;

int main()
{
    cin >> la >> ra >> ta >> lb >> rb >> tb;

    if (la > lb) {
        swap(la, lb);
        swap(ra, rb);
        swap(ta, tb);
    }

    int g = __gcd(ta, tb);
    int k = (lb - la) / g;
    int l = ra - la;

    int ans = 0;
    ans = max(ans, min(la + g * k + l, rb) - max(la + g * k, lb) + 1);
    
    k++;
    ans = max(ans, min(la + g * k + l, rb) - max(la + g * k, lb) + 1);

    cout << ans << endl;
    return 0;
}