数据结构-并查集

简介

并查集(Disjoint-Set)是一种可以动态维护若干个不重叠的集合，并支持合并与查询两种操作的一种数据结构。
就是维护多个集合之间的关系，集合的合并和查询定位（哪个元素属于哪些集合等查询操作），所以并查集主要包括两种操作：

• 合并（Union）：合并两个集合；
• 查询（Find）：查询元素属于哪些集合。

由上面的概念，我们可以知道并查集主要解决以下几个个问题：

• 合并两个或多个集合；
• 判断某一个元素或者多个元素是否属于某个集合

分析

慢union,快find

我们可以用数组来表示数据结构（并查集表示的是多个集合之间的关系，使用map不能直观的描述多个集合的关系），数组的下标代表元素，存储的内容代表所在的集合，如下：

此时假如我们需要将元素2合并到元素1所在集合,则直接使arr[2]=arr[1]就行了

假如我们要将1集合加入到3集合，也就是元素1和元素2加入到3的集合中，则需要将元素1和元素2所在的集合做更改，arr[1]=3,arr[2]=3,合并的时间复杂度为O(n)

这时判断元素1和元素2是否在同一个集合只需要判断数组内值是否相等即可arr[1]==arr[2],相等则说明属于同一个集合，时间复杂度为O(1)
示例代码如下(慢union,快)：

package com.example.demo;

public class Test {

    private static int[] arr = new int[]{0,1,2,3,4,5,6,7};

    public static void main(String[] args) throws Exception {
        System.out.println("元素所在集合初始：" );
        arrToString(arr);
        System.out.println("将元素2合并到元素1所在集合");
        union(2,1);
        arrToString(arr);
        System.out.println("将元素1、2合并到3所在集合");
        union(1,3);
        arrToString(arr);
    }

    /**
     * 查看元素属于哪个集合
     * 时间复杂度为 O（1）
     * @param index
     * @return
     */
    public static int find(int index){
        return arr[index];
    }

    /**
     * 判断两个元素是否属于同一个集合
     * @param first
     * @param second
     * @return
     */
    public static boolean isTogether(int first, int second){
        return find(first) == find(second);
    }

    /**
     * 时间复杂度为 O（n）
     * 将first元素所在集合合并到second元素所在集合
     * @param first
     * @param second
     */
    public static void union(int first, int second){
        int m1 = find(first);
        int m2 = find(second);

        for(int i = 0; i < arr.length;i++){
            if(arr[i] == m1 ){
                arr[i] = m2;
            }
        }

    }

    public static void arrToString(int[] arr){
        if(null == arr || arr.length <= 0){
            return;
        }
        System.out.print("数组元素：");
        for(int i = 0 ; i < arr.length ; i ++){
            System.out.print(i + " " );
        }
        System.out.println("");
        System.out.print("所在集合：");
        for(int c : arr){
            System.out.print(c + " ");
        }
        System.out.println("");
    }

}

输出：
元素所在集合初始：
数组元素：0 1 2 3 4 5 6 7
所在集合：0 1 2 3 4 5 6 7
将元素2合并到元素1所在集合
数组元素：0 1 2 3 4 5 6 7
所在集合：0 1 1 3 4 5 6 7
将元素1、2合并到3所在集合
数组元素：0 1 2 3 4 5 6 7
所在集合：0 3 3 3 4 5 6 7

上面的方法union时间复杂度是O（n）,每次合并都需要把需要合并的集合遍历一遍，当集合内数据很大时肯定是不行的，我们需要对union进行优化

快union,慢find

我们将上面的关系转化为树形结构,改成树形结构时我们需要对数组进行小调整，数组下标依然表示元素，数组内容需要变为父集合。
上面我们将2加入1，则元素2的父集合就是1所在的集合，1加入3则元素1的父集合就是3所在的集合，稍做调整后的数组结为arr[2]=arr[1],arr[1]=arr[3],如图：

树形结构如下图：

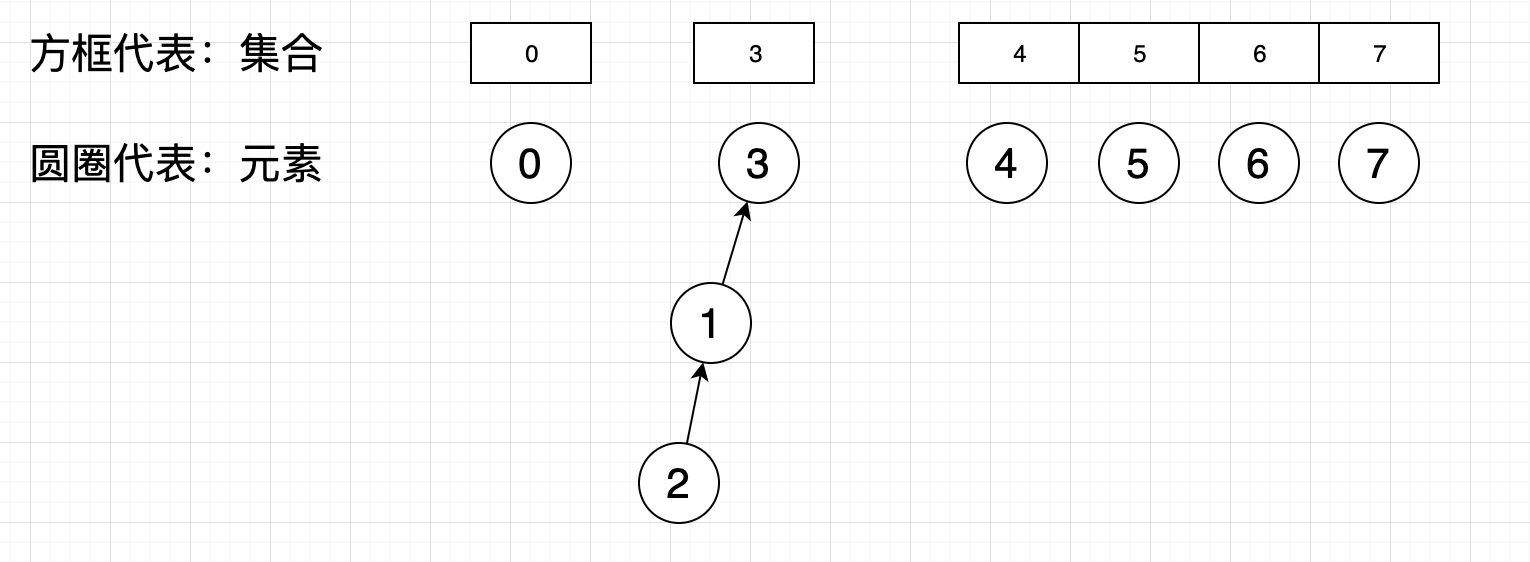
这个时候假如我们将3集合合并到4集合，其实只需要把领头的元素3加入到4集合，元素1，2，3的关系保持不变就可以了，只需要操作一步就完成了合并操作。这个时候数据结构就从数组转变成了树形结构，成功的将union时间复杂度变为了O（1）

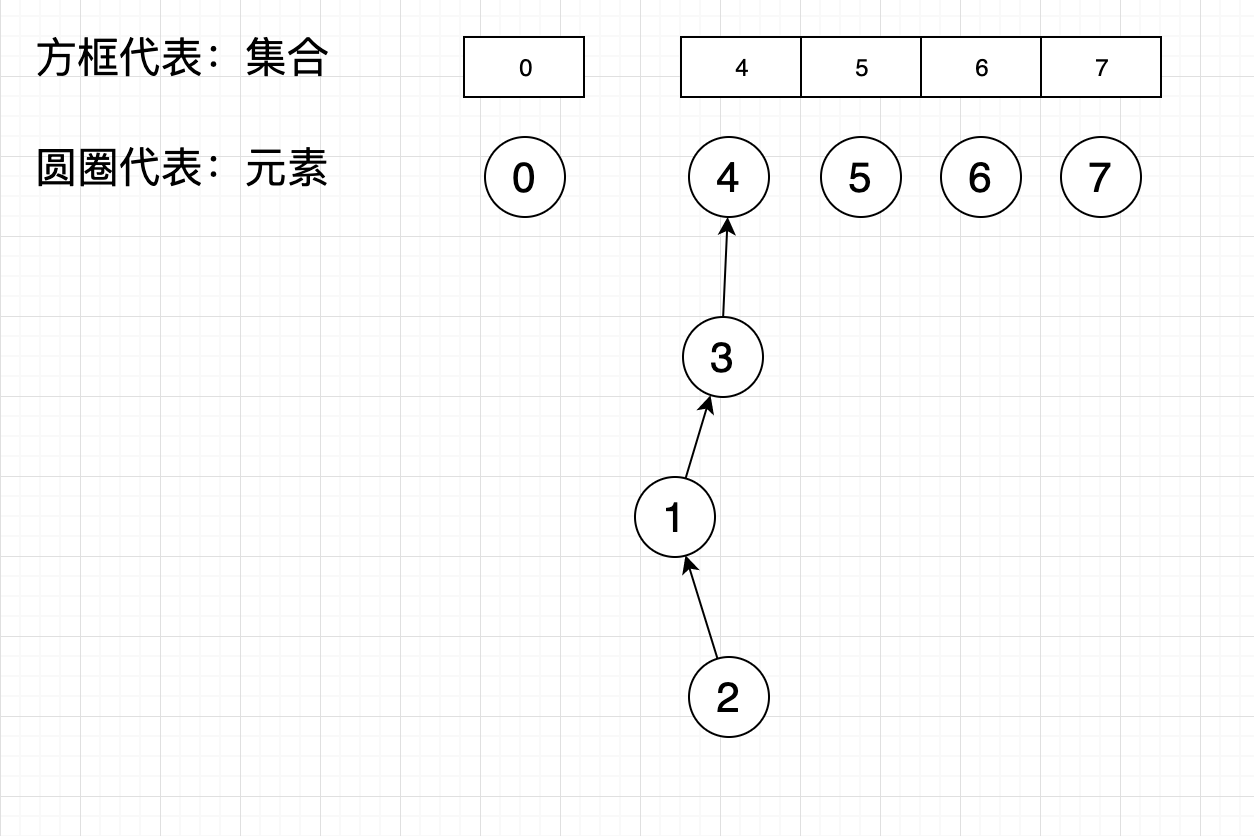
再来看find(1),需要找到顶部元素所在集合（也就是元素4所在集合）即可，时间复杂度取决于树的深度
示例代码：

package com.example.demo;

public class Test2 {

    private static int[] arr = new int[]{0,3,1,3,4,5,6,7};

    public static void main(String[] args) throws Exception {
        System.out.println("元素所在集合初始：");
        arrToString(arr);
        System.out.println("将元素3所在集合合并到元素4所在集合");
        union(3, 4);
        arrToString(arr);
    }

    /**
     * 查看元素属于哪个集合
     * 时间复杂度为 O（1）
     * @param index
     * @return
     */
    public static int find(int index){
        // 判断自己是不是顶部节点 没有父集合就是顶部元素
        while(index != arr[index]){
            //如果不是顶部元素  则往上查找  知道找到顶部元素为止
            //顶部元素所在的集合就是该元素所在的集合
            index = arr[index];
        }
        return index;
    }

    /**
     * 判断两个元素是否属于同一个集合
     * @param first
     * @param second
     * @return
     */
    public static boolean isTogether(int first, int second){
        return find(first) == find(second);
    }

    /**
     * 时间复杂度为 O（n）
     * 将first元素所在集合合并到second元素所在集合
     * @param first
     * @param second
     */
    public static void union(int first, int second){
        int firstRoot = find(first);
        int secondRoot = find(second);
        // 如果所属集合相等则不操作
        if(firstRoot == secondRoot){
            return ;
        }
        // 否则将first元素所在集合的顶部元素所在的父集合指向元素second顶部元素所在的集合，则完成了合并
        arr[firstRoot] = secondRoot;
    }

    public static void arrToString(int[] arr){
        if(null == arr || arr.length <= 0){
            return;
        }
        System.out.print("数组元素：");
        for(int i = 0 ; i < arr.length ; i ++){
            System.out.print(i + " " );
        }
        System.out.println("");
        System.out.print("所在集合：");
        for(int c : arr){
            System.out.print(c + " ");
        }
        System.out.println("");
    }

}

输出：
元素所在集合初始：
数组元素：0 1 2 3 4 5 6 7
所在集合：0 3 1 3 4 5 6 7
将元素3所在集合合并到元素4所在集合
数组元素：0 1 2 3 4 5 6 7
所在集合：0 3 1 4 4 5 6 7

快速union，快速find，基于重量

上面的例子中我们要找到2所在的集合需要把整个集合都遍历一遍，这是因为每次合并时都是往父一级追加，形成了线性链表，上面的优化导致了find方法时间复杂度为集合深度。为了再次优化find方法，我们需要优化树结构的生成规则。既然两个元素合并到一个元素，以上面的例子举例，元素3合并到元素4和元素4合并到元素3其实是一个效果，但是显然元素4合并到元素3更为合理。也就是谁元素多谁为主，元素少的集合合并到元素多的集合中，这样就能降低树的深度提高find效率了

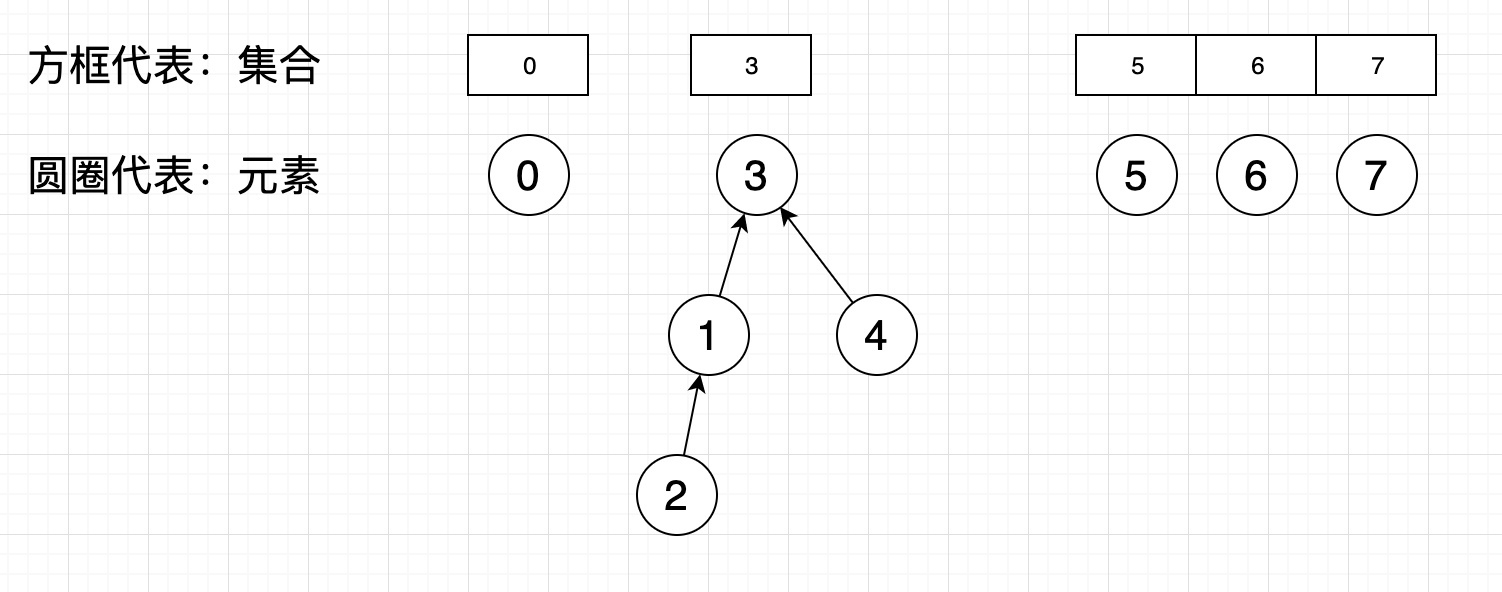
示例代码：

package com.example.demo;

public class Test3 {

    private static int[] arr    = new int[]{0,3,1,3,4,5,6,7};
    private static int[] weight = new int[]{1,1,0,2,1,1,1,1};

    public static void main(String[] args) throws Exception {
        System.out.println("元素所在集合初始：");
        arrToString(arr);
        System.out.println("将元素3所在集合和元素4所在集合合并");
        union(3, 4);
        arrToString(arr);
    }

    /**
     * 查看元素属于哪个集合
     * 时间复杂度为 O（1）
     * @param index
     * @return
     */
    public static int find(int index){
        // 判断自己是不是顶部节点 没有父集合就是顶部元素
        while(index != arr[index]){
            //如果不是顶部元素  则往上查找  知道找到顶部元素为止
            //顶部元素所在的集合就是该元素所在的集合
            index = arr[index];
        }
        return index;
    }

    /**
     * 判断两个元素是否属于同一个集合
     * @param first
     * @param second
     * @return
     */
    public static boolean isTogether(int first, int second){
        return find(first) == find(second);
    }

    /**
     * 时间复杂度为 O（n）
     * 将first元素所在集合合并到second元素所在集合
     * @param first
     * @param second
     */
    public static void union(int first, int second){
        int firstRoot = find(first);
        int secondRoot = find(second);
        // 如果所属集合相等则不操作
        if(firstRoot == secondRoot){
            return ;
        }
        // 取出所在集合元素个数
        int fweight = weight[firstRoot];
        int sweight = weight[secondRoot];
        if(fweight < sweight){
            //若second所在集合元素个数大于first所在集合元素个数
            // 则将first元素加入second元素所在集合
            arr[firstRoot] = secondRoot;
            weight[secondRoot] = sweight + fweight ;
        }else{
            // 于上面相反
            arr[secondRoot] = firstRoot;
            weight[firstRoot] = fweight + sweight;

        }

    }

    public static void arrToString(int[] arr){
        if(null == arr || arr.length <= 0){
            return;
        }
        System.out.print("数组元素：");
        for(int i = 0 ; i < arr.length ; i ++){
            System.out.print(i + " " );
        }
        System.out.println("");
        System.out.print("所在集合：");
        for(int c : arr){
            System.out.print(c + " ");
        }
        System.out.println("");
        System.out.print("集合重量：");
        for(int c : weight){
            System.out.print(c + " ");
        }
        System.out.println("");
    }

}

元素所在集合初始：
数组元素：0 1 2 3 4 5 6 7
所在集合：0 3 1 3 4 5 6 7
集合高度：1 1 0 2 1 1 1 1
将元素3所在集合合并到元素4所在集合
数组元素：0 1 2 3 4 5 6 7
所在集合：0 3 1 3 3 5 6 7
集合重量：1 1 0 3 1 1 1 1

观察上面输出可以看到元素4加入了集合3

快速union，快速find，基于高度(基于秩)

对于上述改进方法，只是单纯的判断集合内元素的个数大小来决定如何合并集合，如果数据结构是如下图时：

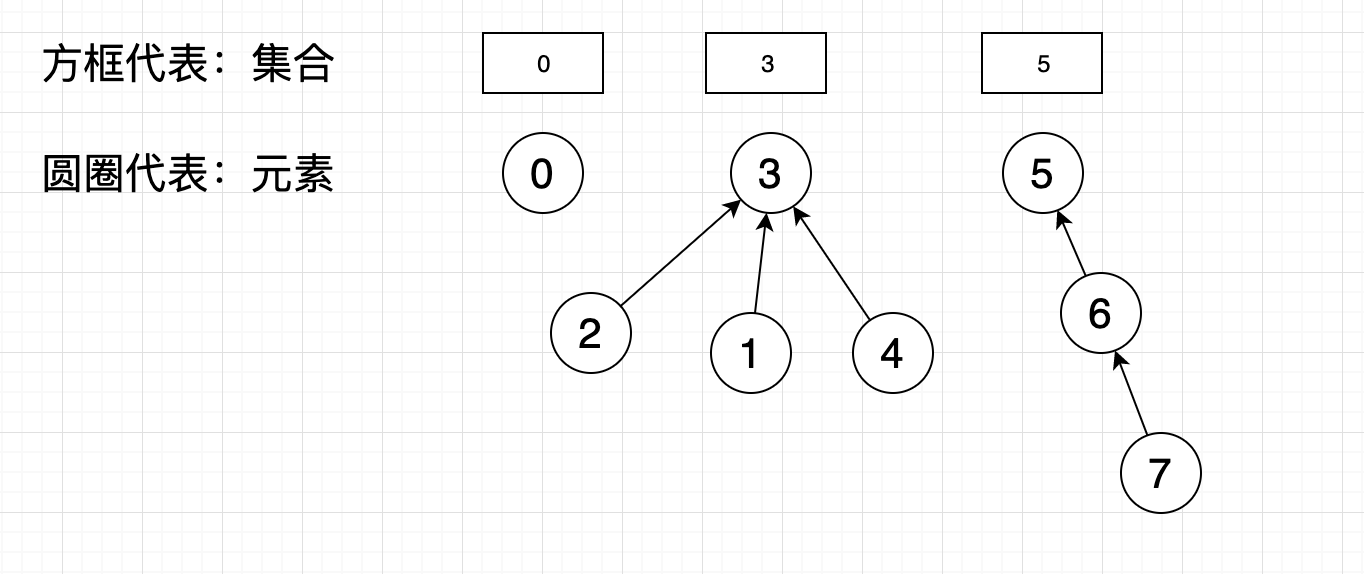
假如按照元素个数谁大合并到谁那则会出现下面的情况

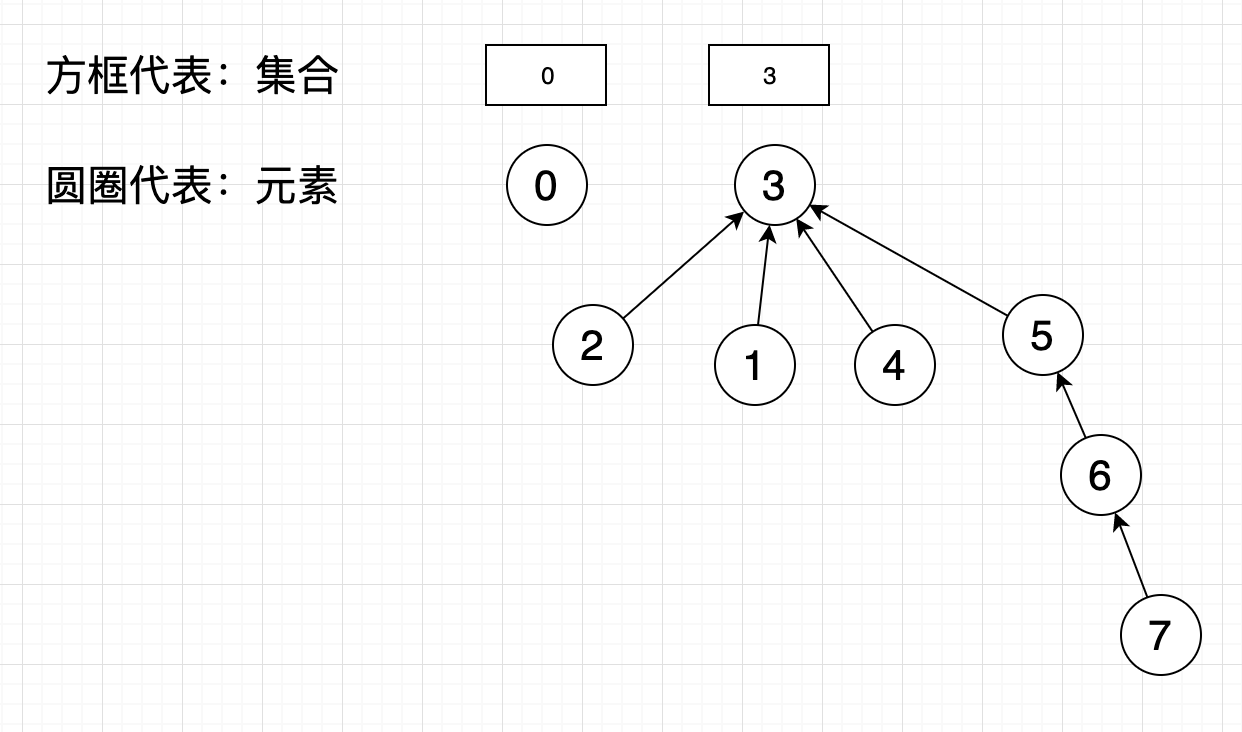
集合5加入了集合3，树的高度变为了4，极端情况下find的时间复杂度会无限接近o(n)(无限接近线性链表的结构)。假如我们按照树的高度来判断合并到哪个集合，上述情况合并会得到：

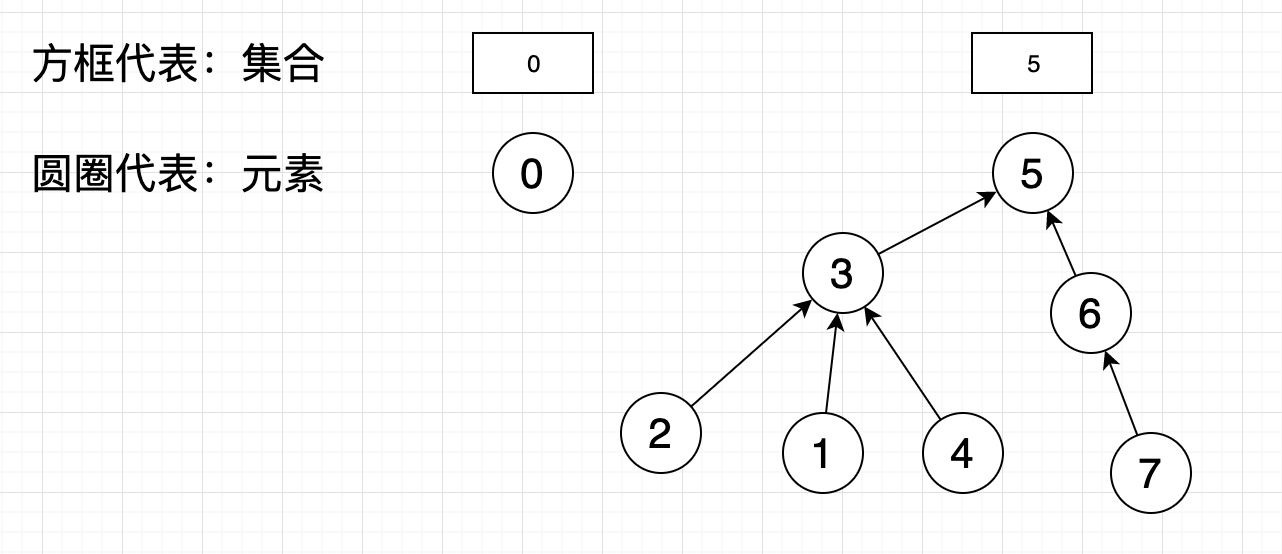
示例代码：

package com.example.demo;

public class Test4 {

    private static int[] arr    = new int[]{0,3,3,3,3,5,5,6};
    private static int[] height = new int[]{1,1,1,2,1,3,2,1};

    public static void main(String[] args) throws Exception {
        System.out.println("元素所在集合初始：");
        arrToString(arr);
        System.out.println("将元素3所在集合和元素5所在集合合并");
        union(3, 5);
        arrToString(arr);
    }

    /**
     * 查看元素属于哪个集合
     * 时间复杂度为 O（1）
     * @param index
     * @return
     */
    public static int find(int index){
        // 判断自己是不是顶部节点 没有父集合就是顶部元素
        while(index != arr[index]){
            //如果不是顶部元素  则往上查找  知道找到顶部元素为止
            //顶部元素所在的集合就是该元素所在的集合
            index = arr[index];
        }
        return index;
    }

    /**
     * 判断两个元素是否属于同一个集合
     * @param first
     * @param second
     * @return
     */
    public static boolean isTogether(int first, int second){
        return find(first) == find(second);
    }

    /**
     * 时间复杂度为 O（n）
     * 将first元素所在集合合并到second元素所在集合
     * @param first
     * @param second
     */
    public static void union(int first, int second){
        int firstRoot = find(first);
        int secondRoot = find(second);
        // 如果所属集合相等则不操作
        if(firstRoot == secondRoot){
            return ;
        }
        // 取出所在集合元素个数
        int fheight = height[firstRoot];
        int sheight = height[secondRoot];
        if(fheight < sheight){
            //若second所在集合高度大于first所在集合高度
            // 则将first元素加入second元素所在集合
            // 高度取决于最高的集合 所以最大高度并不会改变
            arr[firstRoot] = secondRoot;
        }else if(fheight == sheight){
            //若second所在集合高度和first所在集合高度  相等
            // 则将first元素加入second元素所在集合
            // 高度+1
            arr[firstRoot] = secondRoot;
            height[secondRoot] = sheight + 1;
        }else{
            //若second所在集合高度小于first所在集合高度
            // 则将second元素加入first元素所在集合
            // 高度不变
            arr[secondRoot] = firstRoot;
        }

    }

    public static void arrToString(int[] arr){
        if(null == arr || arr.length <= 0){
            return;
        }
        System.out.print("数组元素：");
        for(int i = 0 ; i < arr.length ; i ++){
            System.out.print(i + " " );
        }
        System.out.println("");
        System.out.print("所在集合：");
        for(int c : arr){
            System.out.print(c + " ");
        }
        System.out.println("");
        System.out.print("集合高度：");
        for(int c : height){
            System.out.print(c + " ");
        }
        System.out.println("");
    }

}

输出：
元素所在集合初始：
数组元素：0 1 2 3 4 5 6 7
所在集合：0 3 3 3 3 5 5 6
集合高度：1 1 1 2 1 3 2 1
将元素3所在集合和元素5所在集合合并
数组元素：0 1 2 3 4 5 6 7
所在集合：0 3 3 5 3 5 5 6
集合高度：1 1 1 2 1 3 2 1

最大高度还是3没有变化

路径压缩

针对基于重量的优化，我们可以将叶子节点直接指向父元素的父元素所在集合，这样也能压缩树的高度，提高find性能。这种方法实际上没有改变树的结构，只是直接越级查找了
示例代码：

package com.example.demo;

public class Test32 {

    private static int[] arr    = new int[]{0,3,1,3,4,5,6,7};
    private static int[] weight = new int[]{1,1,0,2,1,1,1,1};

    public static void main(String[] args) throws Exception {
        System.out.println("元素所在集合初始：");
        arrToString(arr);
        System.out.println("将元素3所在集合和元素4所在集合合并");
        union(3, 4);
        arrToString(arr);
    }

    /**
     * 查看元素属于哪个集合
     * 时间复杂度为 O（1）
     * @param index
     * @return
     */
    public static int find(int index){
        // 判断自己是不是顶部节点 没有父集合就是顶部元素
        while(index != arr[index]){
            //如果不是顶部元素  则往上查找  知道找到顶部元素为止
            // 这里查找采用路径压缩法，越过一级往上查找
            index = arr[arr[index]];
        }
        return index;
    }

    /**
     * 判断两个元素是否属于同一个集合
     * @param first
     * @param second
     * @return
     */
    public static boolean isTogether(int first, int second){
        return find(first) == find(second);
    }

    /**
     * 时间复杂度为 O（n）
     * 将first元素所在集合合并到second元素所在集合
     * @param first
     * @param second
     */
    public static void union(int first, int second){
        int firstRoot = find(first);
        int secondRoot = find(second);
        // 如果所属集合相等则不操作
        if(firstRoot == secondRoot){
            return ;
        }
        // 取出所在集合元素个数
        int fweight = weight[firstRoot];
        int sweight = weight[secondRoot];
        if(fweight < sweight){
            //若second所在集合元素个数大于first所在集合元素个数
            // 则将first元素加入second元素所在集合
            arr[firstRoot] = secondRoot;
            weight[secondRoot] = sweight + fweight;
        }else{
            // 于上面相反
            arr[secondRoot] = firstRoot;
            weight[firstRoot] = fweight + sweight;

        }

    }

    public static void arrToString(int[] arr){
        if(null == arr || arr.length <= 0){
            return;
        }
        System.out.print("数组元素：");
        for(int i = 0 ; i < arr.length ; i ++){
            System.out.print(i + " " );
        }
        System.out.println("");
        System.out.print("所在集合：");
        for(int c : arr){
            System.out.print(c + " ");
        }
        System.out.println("");
        System.out.print("集合重量：");
        for(int c : weight){
            System.out.print(c + " ");
        }
        System.out.println("");
    }

}

输出：
元素所在集合初始：
数组元素：0 1 2 3 4 5 6 7
所在集合：0 3 1 3 4 5 6 7
集合重量：1 1 0 2 1 1 1 1
将元素3所在集合和元素4所在集合合并
数组元素：0 1 2 3 4 5 6 7
所在集合：0 3 1 3 3 5 6 7
集合重量：1 1 0 3 1 1 1 1

应用场景：

并查集在很多场景都可以使用，比如地图寻址，im的群查找合并，数据统计等
例如：https://blog.csdn.net/jert159/java/article/details/38617095