Section 1
Finding the probability of an observed sequence
1. Exhaustive search for solution
给定HMM,要找出 observed sequence 的概率。
在 weather model 中,我们有一个 HMM 描述了 weather 以及 weather 和 seaweed states 的关系。如果观察到的连续 3 天,seaweed 状态是 (dry, damp, soggy),则可以将 observations 和 hidden states 的关系绘制成格子性质 trellis:
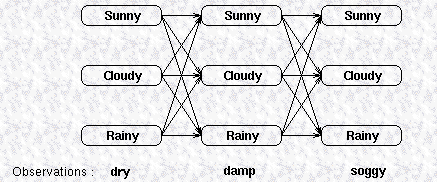
相邻的 column 列之间的概率是由 transition matrix 确定的,每个 column 下边的 observation 在不同的 hidden states (也就是weather)下的概率是由 confusion matrix 决定的。
为了计算 Pr(dry, damp, soggy),一个方法是:
Pr(dry,damp,soggy | HMM) = Pr(dry,damp,soggy | sunny,sunny,sunny) + Pr(dry,damp,soggy | sunny,sunny ,cloudy) + Pr(dry,damp,soggy | sunny,sunny ,rainy) + . . . . Pr(dry,damp,soggy | rainy,rainy ,rainy)
这里的计算相当麻烦,可以利用 概率的时间不变性(time invariance of the probabilities) 进行简化。
2. Reduction of compleity using recursion
假定 T-long observed sequence 是

2a. Partial Probabilities, (a's alpha's)
到达每个中间状态的概率,是所有路径的概率的和。
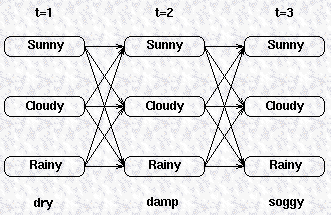
例如:
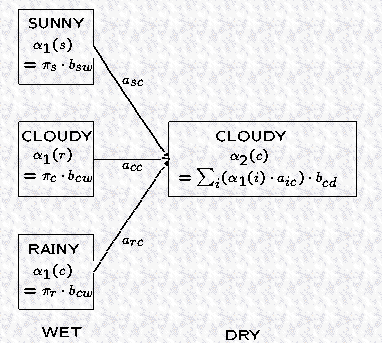
at(j) : partial probability of state j at time t
at(j) = Pr(observation | hiden state is j) * Pr(all paths to state j at time t)
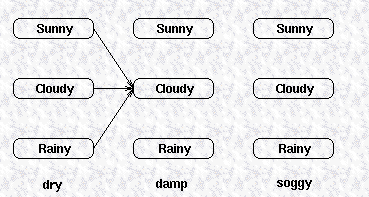
最后一个观测 (observation) 代表了通过所有可能的路径到达这些状态的概率,对于以上例子,final partial probabilities 计算如下:

2b. Calculating a's at time t=1
t = 1 时,没有到这个状态的路径,因此 Pr(state | t = 1) = π(state),因此
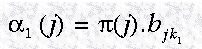
初始状态处于 j 的概率依赖于 状态 j 的概率,以及观察到的状态的概率。
2c. Calculating a's at time t>1

假定第一个状态是已知的,考虑第二项 Pr(all paths to state j at time t)。这一项可以通过计算每个路径的概率,然后再加和。
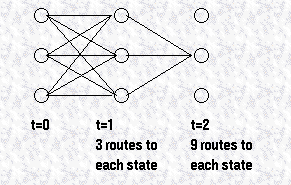
路径的数目随着观察序列的增长呈指数增长,可以通过 at-1来进行计算,也就是:
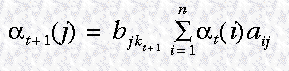
2d. Reduction of computational complexity
对于一个长度为 T 的观测序列,它的 HMM 有 n 个 hidden states, l=(π, A, B)。
遍历的方法,复杂度是指数级,然而通过 forward algorithm,利用上一步计算的结果计算一个新的值,期复杂度是 T的线形级别。
Section 2
Forward algorithm definition
使用 forward algorithm 来计算一个 T 长度的观测序列的概率:
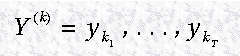
y 代表 observable set 中的元素。
中间的概率可以递归的采用 a1(j) 来算出。
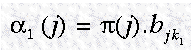
对于t > 1的情况,可以递归求出:
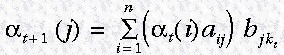
最终所有 partial probabilities 的概率之和给出了观测序列的概率
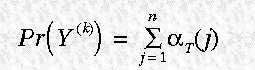
对于天气的例子,t=2时,a对于 cloudy 状态的概率计算如下: