zoukankan      html  css  js  c++  java

  • Directx11学习笔记【五】 基本的数学知识----向量篇

    本文参考dx11龙书 Chapter1 vector algebra(向量代数)

    要想学好游戏编程，扎实的数学知识是尤为重要的，下面将对dx11龙书中有关向量的数学知识做一下总结。

    在数学中，几何向量（也称为欧几里得向量，通常简称向量、矢量），指具有大小（magnitude）和方向（direction）的几何对象，可以形象化地表示为带箭头的线段，箭头所指：代表向量的方向、线段长度：代表向量的大小。

    向量的表示方式一般有3种：

    　　1.代数表示：一般印刷用黑体小写字母α、β、γ…或a、b、c… 等来表示，手写用在a、b、c…等字母上加一箭头表示

    　　2.几何表示：用有向线段表示

    　　3.坐标表示

    （注：directx使用的是左手系，下面不作说明均以左手系为准）

    向量的一些基本操作（部分摘自百度百科）：

    1.向量的模，即向量的长度。

    向量a的模记作|a|。向量的模是非负实数，是可以比较大小的。因为方向不能比较大小，所以向量也就不能比较大小。对于向量来说“大于”和“小于”的概念是没有意义的。例如，“向量AB>向量CD”是没有意义的。

    2.单位向量
    长度为一个单位（即模为1）的向量，叫做单位向。与向量a同向，且长度为单位1的向量，叫做a方向上的单位向量，记作a0，a0=a/|a|。
    3.向量的加减法
    向量的加法满足平行四边形法则和三角形法则。OB+OA=OC。
    a+0=0+a=a。
    向量加法的运算律：
    交换律：a+b=b+a；
    结合律：(a+b)+c=a+(b+c)。
    减法与加法类似
    4.数量积（点积）
    定义：已知两个非零向量a,b。作OA=a,OB=b，则角AOB称作向量a和向量b的夹角，记作〈a,b〉并规定0≤〈a,b〉≤π
    定义：两个向量的数量积（内积、点积）是一个数量（没有方向），记作a·b。若a、b不共线，则a·b=|a|·|b|·cos〈a，b〉（依定义有：cos〈a,b〉=a·b / |a|·|b|）；若a、b共线，则a·b=±∣a∣∣b∣。
    向量的数量积的坐标表示：a·b=x·x'+y·y'。
    向量的数量积的运算律
    a·b=b·a（交换律）
    (λa)·b=λ(a·b)(关于数乘法的结合律)
    （a+b)·c=a·c+b·c（分配律）
    向量的数量积的性质
    a·a=|a|的平方。
    a⊥b〈=〉a·b=0。
    |a·b|≤|a|·|b|。
    5.向量积（叉积）
    定义：两个向量a和b的向量积
    （外积、叉积）是一个向量，记作a×b（这里“×”并不是乘号，只是一种表示方法，与“·”不同，也可记做“∧”）。若a、b不共线，则a×b的模是：∣a×b∣=|a|·|b|·sin〈a，b〉；a×b的方向是：垂直于a和b，且a、b和a×b按这个次序构成右手系。若a、b垂直，则∣a×b∣=|a|*|b|（此处与数量积不同，请注意），若a×b=0，则a、b平行。向量积即两个不共线非零向量所在平面的一组法向量。
    运算法则：运用三阶行列式
    设a,b,c分别为沿x,y,z轴的单位向量
    A=(x1,y1,z1)B=（x2,y2,z2）则A*B=
    a b c
    x1 y1 z1
    x2 y2 z2
    向量的向量积性质：
    ∣a×b∣是以a和b为边的平行四边形面积。
    a×a=0。
    a平行b〈=〉a×b=0
    向量的向量积运算律
    a×b=－b×a
    （λa）×b=λ（a×b）=a×（λb）
    a×（b+c）=a×b+a×c.
    （a+b）×c=a×c+b×c.
    6.向量投影

    给定一个向量u和v，求u在v上的投影向量，如下图。

    假设u在v上的投影向量是u’，且向量u和v的夹角为theta。一个向量有两个属性，大小和方向，我们先确定u’的大小（即长度，或者模），从u的末端做v的垂线，那么d就是u’的长度。而u’和v的方向是相同的，v的方向v/|v|也就是u’的方向。所以有

                              (1)

    再求d的长度。

                          (2)

    最后求cos(theta)

                       (3)

    联合求解方程（1）（2）（3）得到

    这就是最终的投影向量。

    而这个向量的长度d是

    ============================

    以下是旧的推导，也保留。

    XNA MathVectors

    下面介绍一些xna math库中常用的向量结构及方法

    1.向量类型

    有XMVECTOR,XMFLOAT2，XMFLOAT3，XMFLOAT4等几种类型，具体可以看dx11龙书1.6.1节

    在这一章中作者给出使用向量类型应注意的5点：

    (1)、 对局部变量和全局变量，使用XMVECTOR类型；

    (2)、 对类的数据成员，使用XMFLOAT2, XMFLOAT3和XMFLOAT4数据成员；

    (3)、 在进行计算之前，使用载入函数（loading functions）来将XMFLOAT*类型转换成XMVECTOR类型；

    (4)、 用XMVECTOR的实例进行计算；

    (5)、 使用存储函数（storage functions）来将XMVECTOR转换成XMFLOAT*类型

    2.Loading and Storage Methods（载入和存储函数）

    我们用下面的方法来加载数据，从XMFLOAT*到XMVECTOR

    XMVECTOR XMLoadFloat3(CONST XMFLOAT3 *pSource);

    XMVECTOR XMLoadInt3(CONST UINT* pSource);

    XMVECTOR XMLoadColor(CONST XMCOLOR *pSource);

    用下面的方法存储数据，从XMVECTOR到XMFLOAT*

    VOID XMStoreFloat3(XMFLOAT3 *pDestination,FXMVECTOR V);

    ......

    3.Parameter Passing参数传递

    龙书中主要介绍了CXMVECTOR 和FXMVECTOR 这两种参数类型，并告诉了我们在定义函数时，参数类型的注意事项：

    函数的前三个XMVECTOR类型必须是FXMVECTOR，而后面的都是CXMVECTOR。

    4.Constant Vectors常向量

    需要初始化的XMVECTOR常量应该定义为XMVECTORF32类型（用于存储浮点向量）或XMVECTORU32类型（用于存储整数向量）.

    5.Vector Functions一些向量运算有关的函数

    XMVECTOR XMVectorZero();//返回零向量

    XMVECTOR XMVectorSplatOne();//返回(1,1,1,1)

    XMVECTOR XMVectorSet(FLOAT x,FLOAT y,FLOAT z,FLOAT w);//返回(x,y,z,w)

    XMVECTOR XMVectorReplicate(FLOAT s);//返回(s,s,s,s)

    XMVECTOR XMVectorSplatX(FXMVECTOR V);//返回(vx,vx,vx,vx)

    XMVECTOR XMVector3Length(FXMVECTOR V);//返回向量v的模所构成的新的向量，例如向量v模为2，则返回(2,2,2)

    XMVECTOR XMVector3LengthSq(FXMVECTOR V);//模的平方

    XMVECTOR XMVector3Dot(FXMVECTOR V1,FXMVECTOR V2);//点积

    XMVECTOR XMVector3Cross(FXMVECTOR V1,FXMVECTOR V2);//叉积

    XMVECTOR XMVector3Normalize(FXMVECTOR V);//单位化

    XMVECTOR XMVector3Orthogonal(FXMVECTOR V);//得到一个与其垂直的向量

    XMVECTOR XMVector3AngleBetweenVectors(FXMVECTOR V1,FXMVECTOR V2);//两个向量的夹角

    VOID XMVector3ComponentsFromNormal(XMVECTOR* pParallel,XMVECTOR* pPerpendicular,FXMVECTOR V,FXMVECTOR Normal);//向量的投影

    BOOL XMVector3Equal(FXMVECTOR V1,FXMVECTOR V2);//判断两个向量是否相等

    6.Floating-Point Error浮点数计算误差

    用浮点数进行计算（甚至单纯地表示）时，会出现误差，所以等判断相等时，需要定义一个容许误差。

    附：dx11龙书测试的源码及测试结果

    1.

     1 #include <windows.h>
 2 #include <xnamath.h>
 3 #include <iostream>
 4 using namespace std;
 5 
 6 //重载<<操作符
 7 ostream& operator<<(ostream &os, FXMVECTOR v)
 8 {
 9     XMFLOAT3 dest;
10     XMStoreFloat3(&dest, v);
11     os << "(" << dest.x << "," << dest.y << "," << dest.z << ")";
12     return os;
13 }
14 
15 int main()
16 {
17     cout.setf(ios_base::boolalpha);//cout格式化 输入输出bool值可以为true和false
18 
19     //检查是否支持SSE2
20     if (!XMVerifyCPUSupport())
21     {
22         cout << "xna math not supported" << endl;
23         return 0;
24     }
25     XMVECTOR p = XMVectorZero();
26     XMVECTOR q = XMVectorSplatOne();
27     XMVECTOR u = XMVectorSet(1.0f, 2.0f, 3.0f, 0.0f);
28     XMVECTOR v = XMVectorSplatX(u);
29     XMVECTOR w = XMVectorReplicate(-3.5f);
30 
31     cout << "p = " << p << endl;
32     cout << "q = " << q << endl;
33     cout << "u = " << u << endl;
34     cout << "v = " << v << endl;
35     cout << "w = " << w << endl;
36 
37     return 0;
38 }

    2.

     1 #include <windows.h>
 2 #include <xnamath.h>
 3 #include <iostream>
 4 using namespace std;
 5 
 6 ostream& operator<<(ostream &os, FXMVECTOR v)
 7 {
 8     XMFLOAT3 dest;
 9     XMStoreFloat3(&dest, v);
10     os << "(" << dest.x << "," << dest.y << "," << dest.z << ")";
11     return os;
12 }
13 
14 int main()
15 {
16     cout.setf(ios_base::boolalpha);
17     if (!XMVerifyCPUSupport())
18     {
19         cout << "xna math not supported" << endl;
20         return 0;
21     }
22     XMVECTOR n = XMVectorSet(1.0f, 0.0f, 0.0f, 0.0f);
23     XMVECTOR u = XMVectorSet(1.0f, 2.0f, 3.0f, 0.0f);
24     XMVECTOR v = XMVectorSet(-2.0f, 1.0f, -3.0f, 0.0f);
25     XMVECTOR w = XMVectorSet(0.707f, 0.707f, 0.0f, 0.0f);
26 
27     XMVECTOR a = u + v;
28     XMVECTOR b = u - v;
29     XMVECTOR c = 10.0f * u;
30     XMVECTOR L = XMVector3Length(u);
31     XMVECTOR d = XMVector3Normalize(u);
32     XMVECTOR s = XMVector3Dot(u, v);
33     XMVECTOR e = XMVector3Cross(u, v);
34 
35     XMVECTOR projW;
36     XMVECTOR perpW;
37     XMVector3ComponentsFromNormal(&projW, &perpW, w, n);
38 
39     bool equal = XMVector3Equal(projW + perpW, w) != 0;
40     bool notEqual = XMVector3NotEqual(projW + perpW, w) != 0;
41     XMVECTOR angelVec = XMVector3AngleBetweenVectors(projW, perpW);
42     float angleRadians = XMVectorGetX(angelVec);
43     float angleDegrees = XMConvertToDegrees(angleRadians);
44 
45     cout << "u                   = " << u << endl;
46     cout << "v                   = " << v << endl;
47     cout << "w                   = " << w << endl;
48     cout << "n                   = " << n << endl;
49     cout << "a = u + v           = " << a << endl;
50     cout << "b = u - v           = " << b << endl;
51     cout << "c = 10 * u          = " << c << endl;
52     cout << "d = u / ||u||       = " << d << endl;
53     cout << "e = u x v           = " << e << endl;
54     cout << "L  = ||u||          = " << L << endl;
55     cout << "s = u.v             = " << s << endl;
56     cout << "projW               = " << projW << endl;
57     cout << "perpW               = " << perpW << endl;
58     cout << "projW + perpW == w  = " << equal << endl;
59     cout << "projW + perpW != w  = " << notEqual << endl;
60     cout << "angle               = " << angleDegrees << endl;
61 
62     return 0;
63 }

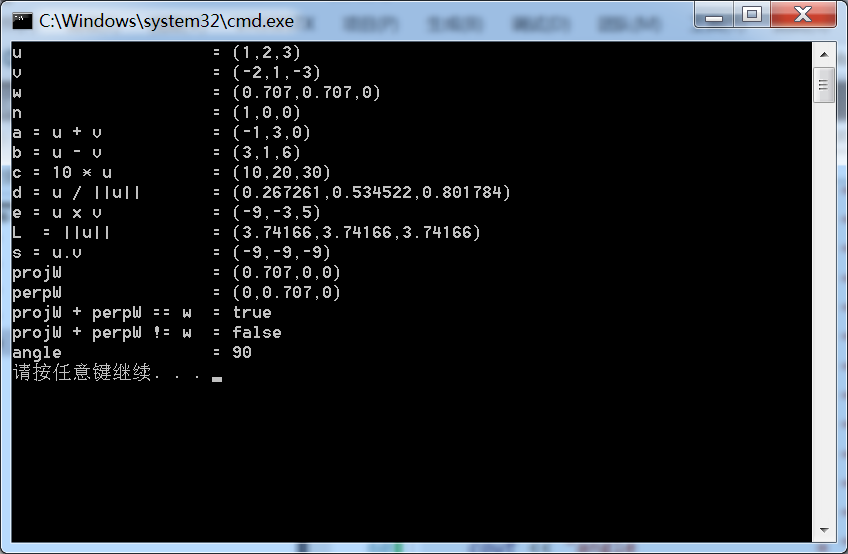
    3.

     1 #include <windows.h> // for FLOAT definition
 2 #include <xnamath.h>
 3 #include <iostream>
 4 using namespace std;
 5 
 6 int main()
 7 {
 8 cout.precision(8);
 9 
10 // Check support for SSE2 (Pentium4, AMD K8, and above).
11 if( !XMVerifyCPUSupport() )
12 {
13 cout << "xna math not supported" << endl;
14 return 0;
15 }
16 
17 XMVECTOR u = XMVectorSet(1.0f, 1.0f, 1.0f, 0.0f);
18 XMVECTOR n = XMVector3Normalize(u);
19 
20 float LU = XMVectorGetX(XMVector3Length(n));
21 
22 // Mathematically, the length should be 1.  Is it numerically?
23 cout << LU << endl;
24 if( LU == 1.0f )
25 cout << "Length 1" << endl;
26 else
27 cout << "Length not 1" << endl;
28 
29 // Raising 1 to any power should still be 1.  Is it?
30 float powLU = powf(LU, 1.0e6f);
31 cout << "LU^(10^6) = " << powLU << endl;
32 }
  • 相关阅读:
    自己写的jQuery放大镜插件效果(一)(采用一张大图和一张小图片的思路)
    javascript 节点操作拷贝节点cloneNode()
    javascript节点操作移出节点removeChild()
    写的一个封拆包代码
    C#_socket拆包_封包_模拟乱序包
    VS2010使用DX报错 VS报错之混合模式程序集是针对“v1.1.4322”版的运行时生成的，在没有配置其他信息的情况下，无法在 4.0 运行时中加载该程序集。
    C#_C++_SDK_WM_KEYDOWN人物卡顿延迟解决方法
    MYSQL游标的使用
    MYSQL异常和错误机制
    CRM中的一个函数，保存一下，别系统被ぅ崩坏就麻烦了.
  • 原文地址：https://www.cnblogs.com/zhangbaochong/p/5236917.html
Copyright © 2011-2022 走看看