转载自:
原文:https://blog.csdn.net/consciousman/article/details/53812818
三角不等式:(在此引用大牛的博客)
B - A <= c (1)
C - B <= a (2)
C - A <= b (3)
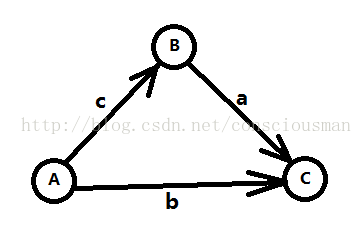
如果要求C-A的最大值,可以知道max(C-A)= min(b,a+c),而这正对应了下图中C到A的最短路。
因此,对三角不等式加以推广,变量n个,不等式m个,要求xn-x1的最大值,便就是求取建图后的最短路。
同样地,如果要求取差分约束系统中xn-x1的最小值,便是求取建图后的最长路。最长路可以通过spfa求出来,只需要改下松弛的方向即可,即if(d[v]
< d[u] + dist(u,v)) d[v] = d[u] +
dist(u,v)。当然我们可以把图中所有的边权取负,求取最短路,两者是等价的。
最长路求解算法证明如下:
http://www.cnblogs.com/g0feng/archive/2012/09/13/2683880.html
最后一点,建图后不一定存在最短路/最长路,因为可能存在无限减小/增大的负环/正环,题目一般会对应于不同的输出。判断差分约束系统是否存在解一般判环即可。
3、差分约束系统的应用
差分约束系统的应用很广,都会有一定的背景,我们只需要根据题意构造出差分约束系统,然后再根据题目的要求求解就行了。
一般题目会有三种情况:(1)、求取最短路 (2)、求取最长路 (3)、判断差分约束系统的解是否存在
当然这三种也可能会相互结合。
差分约束系统的解法如下:
1、 根据条件把题意通过变量组表达出来得到不等式组,注意要发掘出隐含的不等式,比如说前后两个变量之间隐含的不等式关系。
2、 进行建图:
首先根据题目的要求进行不等式组的标准化。
(1)、如果要求取最小值,那么求出最长路,那么将不等式全部化成xi
– xj >= k的形式,这样建立j->i的边,权值为k的边,如果不等式组中有xi – xj >
k,因为一般题目都是对整形变量的约束,化为xi – xj >= k+1即可,如果xi – xj = k呢,那么可以变为如下两个:xi –
xj >= k, xi – xj <= k,进一步变为xj – xi >= -k,建立两条边即可。
(2)、如果求取的是最大值,那么求取最短路,将不等式全部化成xi – xj <= k的形式, 这样建立j->i的边,权值为k的边,如果像上面的两种情况,那么同样地标准化就行了。
(3)、如果要判断差分约束系统是否存在解,一般都是判断环,选择求最短路或者最长路求解都行,只是不等式标准化时候不同,判环地话,用spfa即可,n个点中如果同一个点入队超过n次,那么即存在环。
值得注意的一点是:建立的图可能不联通,我们只需要加入一个超级源点,比如说求取最长路时图不联通的话,我们只需要加入一个点S,对其他的每个点建立一条权值为0的边图就联通了,然后从S点开始进行spfa判环。最短路类似。
3、 建好图之后直接spfa或bellman-ford求解,不能用dijstra算法,因为一般存在负边,注意初始化的问题。
1 #include"iostream" 2 #include"algorithm" 3 #include"cstring" 4 #include"cstdio" 5 #include"queue" 6 #include"stack" 7 using namespace std; 8 9 int n,m; 10 const int nn =150010; 11 12 int link[nn],w[nn],son[nn],nxt[nn]; 13 int tote; 14 15 inline void edge(int x,int y,int z) 16 { 17 ++tote; 18 nxt[tote]=link[x]; 19 link[x]=tote; 20 son[tote]=y; 21 w[tote]=z; 22 23 } 24 25 int vis[30010]; 26 int dis[30010]; 27 deque<int > q; 28 stack<int >s; 29 30 void spfa() 31 { 32 33 34 memset(dis,0x3f,sizeof dis); 35 memset(vis,0,sizeof vis); 36 dis[1]=0; 37 s.push(1); 38 while (!s.empty()) 39 { 40 int t=s.top();s.pop(),vis[t]=0; 41 42 43 for (int i=link[t];i;i=nxt[i]) 44 { 45 int so = son[i]; 46 if (dis[so]>dis[t]+w[i]) 47 { 48 dis[so] = dis[t] + w[i]; 49 if (!vis[so]) 50 { 51 52 53 vis[so]=1; 54 s.push(so); 55 56 } 57 } 58 } 59 } 60 printf("%d ",dis[n]); 61 62 } 63 64 65 66 int main() 67 { 68 while (cin>>n>>m) 69 { 70 memset(link,0,sizeof link); 71 72 for (int i=1;i<=m;i++) 73 { 74 // cout<<i<<endl; 75 int a,b,c; 76 scanf("%d%d%d",&a,&b,&c); 77 edge(a,b,c); 78 } 79 spfa(); 80 } 81 82 83 }
队列版本:
1 #include"iostream" 2 #include"algorithm" 3 #include"cstring" 4 #include"cstdio" 5 #include"queue" 6 #include"stack" 7 using namespace std; 8 9 int n,m; 10 const int nn =150010; 11 12 int link[nn],w[nn],son[nn],nxt[nn]; 13 int tote; 14 15 inline void edge(int x,int y,int z) 16 { 17 ++tote; 18 nxt[tote]=link[x]; 19 link[x]=tote; 20 son[tote]=y; 21 w[tote]=z; 22 23 } 24 25 int vis[30010]; 26 int dis[30010]; 27 deque<int > q; 28 stack<int >s; 29 30 void spfa() 31 { 32 33 34 35 memset(dis,0x3f,sizeof dis); 36 memset(vis,0,sizeof vis); 37 dis[1]=0; 38 39 q.push_back(1); 40 while (!q.empty()) 41 { 42 int t= q.front();q.pop_front(); vis[t]=0; 43 if (!q.empty()&&dis[q.front()]>dis[q.back()]) swap(q.front(),q.back()); 44 for (int i=link[t];i;i=nxt[i]) 45 { 46 int so = son[i]; 47 if (dis[so]>dis[t]+w[i]) 48 { 49 dis[so] = dis[t] + w[i]; 50 51 if (!vis[so]) 52 { 53 if (!q.empty()&&dis[so]<dis[q.front()]) q.push_front(so); 54 else q.push_back(so); 55 56 57 vis[so]=1; 58 if (!q.empty()&&dis[q.front()]>dis[q.back()]) swap(q.front(),q.back()); 59 60 } 61 } 62 } 63 } 64 printf("%d ",dis[n]); 65 66 } 67 68 69 70 int main() 71 { 72 while (cin>>n>>m) 73 { 74 memset(link,0,sizeof link); 75 76 for (int i=1;i<=m;i++) 77 { 78 // cout<<i<<endl; 79 int a,b,c; 80 scanf("%d%d%d",&a,&b,&c); 81 edge(a,b,c); 82 } 83 spfa(); 84 } 85 86 87 }