myleecode

目录

• myleecode
  • 1.冒泡排序
• 2.快速排序
• 3.进度条打印
• 4.打印 九九乘法表
• 5.打印 金字塔
• 6.接雨滴
• 7.一行代码实现1-100个数相加
• 8.如何在不使用内置方法强制转换的情况将一字符串形式的纯数字转换成整型类型。
• 9.求斐波那契数列第n项的值。
• 10.机器人在m*n的网格上总行走路径数（动态规划）

myleecode

1.冒泡排序

#冒泡排序 

import  time
nums=[40,23,14,35,3,5,12,44,65,21]
def bubble_sort(nums):
    for i in range(len(nums)-1):
        for j in range(len(nums)-i-1):
            if nums[j]>nums[j+1]:
                nums[j],nums[j+1]=nums[j+1],nums[j]
    return nums
start=time.time()
res=bubble_sort([40,23,14,35,3,5,12,44,65,21])
time.sleep(1)
t=time.time()-start
print(res,t)  #1.0000569820404053
'''
打印结果
[3, 5, 12, 14, 21, 23, 35, 40, 44, 65] 1.0000569820404053
'''


# 基于冒泡排序求取求最大值（不使用列表的内置方法sort）

def max_value(nums):
    count=0
    for i in range(len(nums)-1):
        for j in range(len(nums)-i-1):
            if nums[i]>nums[i+1]:
                nums[i],nums[i+1]=nums[i+1],nums[i]
    return nums[len(nums)-1]
res=max_value([40,23,14,35,3,5,12,44,65,21])
print(res)
'''
打印结果
65
'''
#简单版本求最大值（不使用列表中sort方法）
l=[40,23,14,355,3,5,12,44,65,21]
for i in range(len(l)-1):
   if l[i]>l[i+1]:
       l[i],l[i+1]=l[i+1],l[i]
print(l[len(l)-1])
'''
打印结果
355
'''

2.快速排序

"""快速排序"""
def quick_sort(data):
    if len(data) >= 2:  # 递归入口及出口
        mid = data[len(data) // 2]  # 选取基准值，也可以选取第一个或最后一个元素
        left, right = [], []  # 定义基准值左右两侧的列表
        data.remove(mid)  # 从原始数组中移除基准值
        for num in data:
            if num >= mid:
                right.append(num)
            else:
                left.append(num)
        return quick_sort(left) + [mid] + quick_sort(right)
    else:
        return data

# 示例：
array = [2, 41, 5, 7, 1, 120, 6, 15, 5, 2, 7, 9, 10, 15, 9, 5, 12]
print(quick_sort(array))

# 输出为[1, 2, 2, 3, 4, 5, 5, 6, 7, 7, 9, 9, 10, 12, 15, 15, 17]

3.进度条打印

# 方法一：
import time
start = time.time()
count = 100
for i in range(count+1):
    print(f'
[{i*">"}：{(count-i)*"-"}]已加载：{i}% ','共用时：',time.time()-start,'s',end='')
    time.sleep(0.1)
print()
print('加载成功！')

# 方法二：
import time

scale=50
print('执行开始'.center(scale//2,'-'))
start=time.perf_counter()
for i in range(scale+1):
    a='*'*i
    b='.'*(scale-i)
    c=(i/scale)*100
    dur=time.perf_counter()-start
    print('
{:3.0f}%[{}->{}]{:.2f}s'.format(c,a,b,dur),end='')
    time.sleep(0.1)
print('
'+'执行结束'.center(scale//2,'-'))

4.打印 九九乘法表

# 方法一：
for i in range(1,10):
    for j in range(1,i+1):  # 内存循环的range条件是根据外层循环决定的
        print('%s*%s=%s'%(i,j,i*j),end=' ')
    print()
    
# 方法二： 一行代码实现99乘法表
print('
'.join([' '.join(['%s*%s=%s'%(y,x,y*x)for y in range(1,x+1)])for x in range(1,10)]))

5.打印 金字塔

max_level = 10
for current_level in range(1,max_level+1):
    # 打印空格
    for i in range(max_level-current_level):
        print(' ',end='')
    # 打印信号
    for j in range(2*current_level-1):
        print('*',end='')
    print()

6.接雨滴

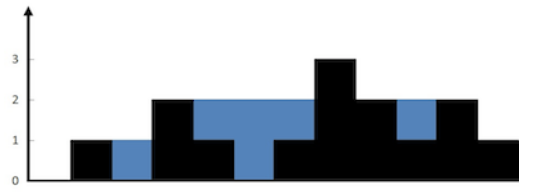
	给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

)

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）

l=[0,2,0,0,4,5,2,0,4,3,2,1,4,5,5]
def trap( height):
    if len(height) <= 1:
        return 0
    max_height = 0
    max_height_index = 0
    # 找到最高点
    for i in range(len(height)):
        h = height[i]
        if h > max_height:
            max_height = h
            max_height_index = i
    area = 0
    # 从左边往最高点遍历
    tmp = height[0]
    for i in range(max_height_index):
        if height[i] > tmp:
            tmp = height[i]
        else:
            area = area + (tmp - height[i])
    # 从右边往最高点遍历
    tmp = height[-1]
    for i in reversed(range(max_height_index + 1, len(height))):
        if height[i] > tmp:
            tmp = height[i]
        else:
            area = area + (tmp - height[i])
    return area
print(trap(l))

7.一行代码实现1-100个数相加

from functools import reduce

print(reduce(lambda x,y:x+y,[i for i in range(1,101)]))

# res=(i for i in range(1,101))
# print(res)  # <generator object <genexpr> at 0x0000000009F6B888> 生成器

8.如何在不使用内置方法强制转换的情况将一字符串形式的纯数字转换成整型类型。

#  方法1  利用ord将十进制数字转换成ASCII码表对应的序号（整型），再与0对应的序号进行相减，得到其对应位数的数字，在进行累加和。
def convert_to_int(str):
    s=0
    for i in str:
        s*=10
        tmp = ord(i) - ord('0')
        s += tmp
    return s
val = convert_to_int('4321')
print(val,type(val))
# 1234 <class 'int'>

res=ord('0')
print(res,type(res))
48 <class 'int'>

# 方法2 主要思想是倒置原字符串，for循环倒置字符串，利用另一相等的整数累加和得到整型123，其本质并不是原字符数字进行的转换。
s='123'
s=s[::-1]
num=0
for k,v in enumerate(s):
    for j in range(0,10):
        if v == str(j):
            num += j * (10**k)
print(num,type(num))
#  123 <class 'int'>

# 方法3  
s='123'
s=s[::-1]
num=0
for k,v in enumerate(s):
    t="%s * 1"%v
    # print(type(v))  # <class 'str'>
    n=eval(t)  # <class 'int'>
    print(n,type(n))
    num += n * (10 ** k)
print(num,type(num))

#  123 <class 'int'>


# 方法四 假如直接用内置方法强转有3中方法：
1).
print(type(eval('12')))
2).
print(type(int('12')))
3).倒模块
from ast import literal_eval
print(type(literal_eval('12')))

'''
<class 'int'>
<class 'int'>
<class 'int'>
'''

# 9.基于生成器

def add(n,i):
    return n+i
def test():
    for i in range(4):
        yield i
g=test()
for n in [1,10]:
    g=(add(n,i) for i in g)
    # 第一次for循环g=(add(n,i) for i in test())
    # 第二次for循环g=(add(n,i) for i in (add(n,i) for i in test()))
res=list(g)

# i = 0
# for i in range(8):
#   pass
# print(i)

g = (add(n, i) for i in g)
g = (add(n, 0), add(n, 1), add(n, 2), add(n, 3))
g = (add(n, i) for i in (add(n, 0), add(n, 1), add(n, 2), add(n, 3)))
g = (add(n,add(n,0)),add(n,add(n,1)),add(n,add(n,2)),add(n,add(n,3)))

# 10.基于匿名函数
## 方式1：
def index():

    return [lambda x, i=i: i*x for i in range(4)]

print([m(2) for m in index()]) 


方式2：把其改成有名函数

def index():
    l1=[]
    l2=[]
    for i in range(4):
        def func(x,i=i):
            return i*x
        l1.append(func)
    for m in l1:  # 一个个不同内存地址的函数名func
        l2.append(m(2))
    print(l2)  
index() 
 
'''
[0, 2, 4, 6]
'''

9.求斐波那契数列第n项的值。

# 方式1：简单递归
def fib(n):
    if n < 2:
        return n
    else:
        return fib(n-1) + fib(n-2)
if __name == "__main__":
    result = fib(100)  # 你等到天荒地老，他还没有执行完
    # 如上所示，代码简单易懂，然而这代码却极其低效。先不说这种递归的方式造成栈空间极大浪费，就仅仅是该算法的时间复杂度已经属于O（2^n）了。指数级别时间复杂度的算法跟不能用没啥区别！
    
    
# 方式2：动态规划
def fib(n):
    results - list(range(n+1))  # 用于缓存以往结果，以便复用（目标2）
    for i in range(n+1):  # 按照顺序从小往大算（目标2）
        if i < 2:
            results[i] = i
        else:
            # 使用状态转移方程（目标1）， 同时复用以往结果（目标2）
            results[i] = results[i-1] + results[i-2]
        return results[-1]
    
if __name == "__main__":
    result = fib(100) # 秒算
                        

10.机器人在m*n的网格上总行走路径数（动态规划）

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

例如，上图是一个7 x 3 的网格。有多少可能的路径？

解这题，如前所述，我们需要完成三个子目标

1. 建立状态转移方程。该题就难在这里，这一步搞不定基本上就GG了。实际上，如图3所示，第i行第j列的格子的路径数，是等于它左边格子和上面格子的路径数之和：

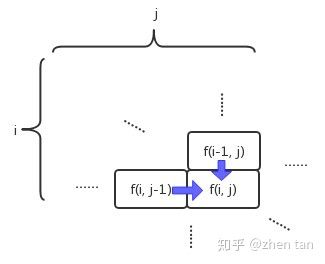
2.缓存并复用以往结果。与之前说的一堆数列不同，这里的中间结果可以构成一个二维数列（如上图），所以需要用二维的数组或者列表来存储。

3.按顺序从小往大算。这次有两个维度，所以需两个循环，分别逐行和逐列让问题从小规模到大规模计算。

代码实现：

# m是行数，n是列数
def count_paths(m,n):
    results = [[1]*n]*m  # 将二维列表初始化为1，以便之后用于缓存（目标2）
    # 题外话：results的空间复杂度不是O（nm），是O（n）
    
    # 第0行和第0列的格子路径数显然均取值为1，所以跳过
    for i in range(1,m):  # 外循环逐行集散（目标3）
        for j in range(1,n):  # 内循环逐行计算（目标3）
            # 状态方程（目标1），以及中间结果复用（目标2）
            results[i][j] = results[i-1][j] + results[i][j-i]
            
    return results[-1][-1]


if __name == "__main__":
    result = count_paths(7,3)  # 结果为28