codeforces 558C C. Amr and Chemistry(bfs)

题目链接：

C. Amr and Chemistry

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Amr loves Chemistry, and specially doing experiments. He is preparing for a new interesting experiment.

Amr has n different types of chemicals. Each chemical i has an initial volume of ai liters. For this experiment, Amr has to mix all the chemicals together, but all the chemicals volumes must be equal first. So his task is to make all the chemicals volumes equal.

To do this, Amr can do two different kind of operations.

• Choose some chemical i and double its current volume so the new volume will be 2ai
• Choose some chemical i and divide its volume by two (integer division) so the new volume will be 

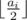
Suppose that each chemical is contained in a vessel of infinite volume. Now Amr wonders what is the minimum number of operations required to make all the chemicals volumes equal?

Input

The first line contains one number n (1 ≤ n ≤ 105), the number of chemicals.

The second line contains n space separated integers ai (1 ≤ ai ≤ 105), representing the initial volume of the i-th chemical in liters.

Output

Output one integer the minimum number of operations required to make all the chemicals volumes equal.

Examples

input

3
4 8 2

output

2

input

3
3 5 6

output

5

Note

In the first sample test, the optimal solution is to divide the second chemical volume by two, and multiply the third chemical volume by two to make all the volumes equal 4.

In the second sample test, the optimal solution is to divide the first chemical volume by two, and divide the second and the third chemical volumes by two twice to make all the volumes equal 1.

题意：

给一个数组,问把这些数全都变成一个数需要多少步操作,两种操作,一种是*2,一种是/2;

思路：

bfs找到一个数能变成的其它数和步数,所有的数操作完后,遍历1~1e5找到有多少个数能变成这个数(等于n的才符合要求),然后在这等于n的中间找到一个总操作数最小的那个;

AC代码：

/*
2014300227     558C - 8    GNU C++11    Accepted    202 ms    3756 KB
*/
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+4;
typedef long long ll;
const double PI=acos(-1.0);
int n,a[N],num[N],vis[N],flag[N];
map<int,int>mp;
struct node
{
    int x,step;
};
queue<node>qu;
queue<int>q;
void solve(int fx)
{
    node ne;
    ne.x=fx;
    ne.step=0;
    qu.push(ne);
    flag[fx]=1;
    while(!qu.empty())
    {
        int fy=qu.front().x,sum=qu.front().step;
        num[fy]+=sum;
        vis[fy]++;
        if(fy*2<=1e5&&flag[fy*2]==0)
        {
            ne.x=fy*2;
            ne.step=sum+1;
            qu.push(ne);
            flag[fy*2]=1;
        }
        if(fy/2>=1&&flag[fy/2]==0)
        {
            ne.x=fy/2;
            ne.step=sum+1;
            qu.push(ne);
            flag[fy/2]=1;
        }
        q.push(fy);
        qu.pop();
    }
    while(!q.empty())flag[q.front()]=0,q.pop();
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        solve(a[i]);
    }
    int ans=2e9;
    for(int i=1;i<=1e5;i++)
    {
        if(vis[i]==n)
        {
            ans=min(ans,num[i]);
        }
    }
    cout<<ans<<endl;


    return 0;
}