codeforces 587B B. Duff in Beach(dp)

题目链接：

B. Duff in Beach

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

While Duff was resting in the beach, she accidentally found a strange array b0, b1, ..., bl - 1 consisting of l positive integers. This array was strange because it was extremely long, but there was another (maybe shorter) array, a0, ..., an - 1 that b can be build from a with formula: bi = ai mod n where a mod b denoted the remainder of dividing a by b.

Duff is so curious, she wants to know the number of subsequences of b like bi1, bi2, ..., bix (0 ≤ i1 < i2 < ... < ix < l), such that:

• 1 ≤ x ≤ k
• For each 1 ≤ j ≤ x - 1, 
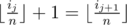
• For each 1 ≤ j ≤ x - 1, bij ≤ bij + 1. i.e this subsequence is non-decreasing.

Since this number can be very large, she want to know it modulo 10^9 + 7.

Duff is not a programmer, and Malek is unavailable at the moment. So she asked for your help. Please tell her this number.

Input

The first line of input contains three integers, n, l and k (1 ≤ n, k, n × k ≤ 10^6 and 1 ≤ l ≤ 10^18).

The second line contains n space separated integers, a0, a1, ..., an - 1 (1 ≤ ai ≤ 10^9 for each 0 ≤ i ≤ n - 1).

Output

Print the answer modulo 1 000 000 007 in one line.

Examples

input

3 5 3
5 9 1

output

10

input

5 10 3
1 2 3 4 5

output

25

Note

In the first sample case, 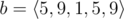. So all such sequences are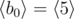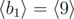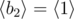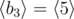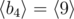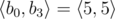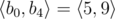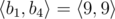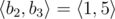: , , , , , , , ,  and .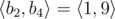

题意：

给一个数组a,然后循环产生长为l的数组,问满足题目给的条件的子序列有多少个;满足的条件为要求不单调递减,而且最长为k,且每相邻的两个来自相邻的段;

思路：

dp[i][j]表示以第i个数结尾的长为j的子序列的个数;转移方程为dp[i][j]=∑dp[x][j-1](满足a[x]<=a[i]所有x);由于n,k的范围太大,所以可以取一维的数组;

dp[i]=∑dp[x](a[x]<=a[i])每层j求完就把答案更新到ans中,还有一个难点就是l%n>0的时候,有前边记录的dp[i]可以把l%n部分求出来;

AC代码：

/*
2014300227    587B - 19    GNU C++11    Accepted    311 ms    33484 KB
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+4;
int n,k,b[N],vis[N];
ll l,dp[N],temp[N];
const ll mod=1e9+7;
struct node
{
    friend bool operator< (node x,node y)
    {
        if(x.a==y.a)return x.pos<y.pos;
        return x.a<y.a;
    }
    int a,pos;
};
node po[N];
int main()
{

    cin>>n>>l>>k;
    for(int i=0;i<n;i++)
    {
        scanf("%d",&po[i].a);
        po[i].pos=i;
    }
    sort(po,po+n);
    po[n].a=po[n-1].a+10;
    for(int i=n-1;i>=0;i--)
    {
        if(po[i].a==po[i+1].a)vis[i]=vis[i+1];//vis[i]记录与a[i]相等的最后一个数的位置;
        else vis[i]=i;
        b[po[i].pos]=i;//把位置还原
    }
    for(int i=0;i<n;i++)
    {
        dp[i]=1;
    }
    ll ans=l,sum,fn=(ll)n;
    ans%=mod;
    for(int i=2;i<=k;i++)
    {
        temp[0]=dp[0];
        for(int j=1;j<n;j++)
        {
            temp[j]=temp[j-1]+dp[j];//temp[j]用来过渡;
            temp[j]%=mod;
        }
        sum=0;
        for(int j=0;j<n;j++)
        {
            dp[j]=temp[vis[j]];
            sum+=dp[j];
            sum%=mod;
        }
        if(l%fn==0)
        {
            if(i<=l/fn)
            {
                ans+=((l/fn-i+1)%mod)*sum;
                ans%=mod;
            }
        }
        else
        {
            if(i<=l/fn)
            {
                ans+=((l/fn-i+1)%mod)*sum;
                ans%=mod;
                sum=0;
                for(int j=0;j<l%fn;j++)
                {
                    sum+=dp[b[j]];
                    sum%=mod;
                }
                ans+=sum;
                ans%=mod;
            }
            else if(i==l/fn+1)
            {
                sum=0;
                for(int j=0;j<l%fn;j++)
                {
                    sum+=dp[b[j]];
                    sum%=mod;
                }
                ans+=sum;
                ans%=mod;
            }
        }
    }
    cout<<ans%mod<<"
";
    return 0;
}