题目链接:
Rikhail Mubinchik believes that the current definition of prime numbers is obsolete as they are too complex and unpredictable. A palindromic number is another matter. It is aesthetically pleasing, and it has a number of remarkable properties. Help Rikhail to convince the scientific community in this!
Let us remind you that a number is called prime if it is integer larger than one, and is not divisible by any positive integer other than itself and one.
Rikhail calls a number a palindromic if it is integer, positive, and its decimal representation without leading zeros is a palindrome, i.e. reads the same from left to right and right to left.
One problem with prime numbers is that there are too many of them. Let's introduce the following notation: π(n) — the number of primes no larger than n, rub(n) — the number of palindromic numbers no larger than n. Rikhail wants to prove that there are a lot more primes than palindromic ones.
He asked you to solve the following problem: for a given value of the coefficient A find the maximum n, such that π(n) ≤ A·rub(n).
The input consists of two positive integers p, q, the numerator and denominator of the fraction that is the value of A (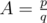 ,
, 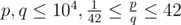 ).
).
If such maximum number exists, then print it. Otherwise, print "Palindromic tree is better than splay tree" (without the quotes).
1 1
40
1 42
1
6 4
172
题意:
问满足pi[n]/rub[n]<=p/q的最大的n是多少;
思路:
pi[i]和rub[i]都随着i的增大而增大,且pi[i]/rub[i]的值也随着增大,(小于10的数特殊);p/q给有范围,可以算一下大约1200000时pi[i]/rub[i]已经大约42了;所以暴力找到那个最大的n;
AC代码:
/*2014300227 569C - 28 GNU C++11 Accepted 61 ms 14092 KB*/ #include <bits/stdc++.h> using namespace std; const int N=12e5+4; typedef long long ll; const double PI=acos(-1.0); int p,q,pi[N],vis[N],rub[N]; void get_pi()//素数筛+dp得到pi[i] { memset(pi,0,sizeof(pi)); pi[1]=0; for(int i=2;i<N;i++) { if(!pi[i]) { for(int j=2;j*i<N;j++) { pi[i*j]=1; } pi[i]=pi[i-1]+1; } else pi[i]=pi[i-1]; } } int is_pal(int x)//判断一个数是不是回文数; { int s=0,y=x; while(y) { s*=10; s+=y%10; y/=10; } if(s==x)return 1; return 0; } void get_rub() { rub[0]=0; for(int i=1;i<N;i++) { if(is_pal(i))rub[i]=rub[i-1]+1; else rub[i]=rub[i-1]; } } int check(int x) { if(pi[x]*q<=p*rub[x])return 1; return 0; } int get_ans() { int ans=0; for(int i=1;i<N;i++) { if(check(i))ans=i; } if(ans==0)printf("Palindromic tree is better than splay tree "); else printf("%d ",ans); } int main() { get_pi(); get_rub(); //cout<<pi[1200000]*1.0/(rub[1200000]*1.0); scanf("%d%d",&p,&q); get_ans(); return 0; }