题目链接:
Mashmokh's boss, Bimokh, didn't like Mashmokh. So he fired him. Mashmokh decided to go to university and participate in ACM instead of finding a new job. He wants to become a member of Bamokh's team. In order to join he was given some programming tasks and one week to solve them. Mashmokh is not a very experienced programmer. Actually he is not a programmer at all. So he wasn't able to solve them. That's why he asked you to help him with these tasks. One of these tasks is the following.
A sequence of l integers b1, b2, ..., bl (1 ≤ b1 ≤ b2 ≤ ... ≤ bl ≤ n) is called good if each number divides (without a remainder) by the next number in the sequence. More formally 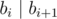 for all i (1 ≤ i ≤ l - 1).
for all i (1 ≤ i ≤ l - 1).
Given n and k find the number of good sequences of length k. As the answer can be rather large print it modulo 1000000007(10^9 + 7).
The first line of input contains two space-separated integers n, k (1 ≤ n, k ≤ 2000).
Output a single integer — the number of good sequences of length k modulo 1000000007 (10^9 + 7).
3 2
5
6 4
39
2 1
2
In the first sample the good sequences are: [1, 1], [2, 2], [3, 3], [1, 2], [1, 3].
题意:
给出这么多数[1,n],问能形成长为l的数列满足b[i]|b[i+1]的方案数;
思路:
dp[i][j]表示长为i,以j结尾的方案数,
dp[i+1][j]=∑dp[i][k],k为j的因数;
AC代码:
#include <bits/stdc++.h> using namespace std; #define Riep(n) for(int i=1;i<=n;i++) #define Riop(n) for(int i=0;i<n;i++) #define Rjep(n) for(int j=1;j<=n;j++) #define Rjop(n) for(int j=0;j<n;j++) #define mst(ss,b) memset(ss,b,sizeof(ss)); typedef long long LL; const LL mod=1e9+7; const double PI=acos(-1.0); const int inf=0x3f3f3f3f; const int N=2e5+6; LL dp[2002][2002]; int main() { int n,k; scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) { dp[1][i]=1; } for(int i=1;i<=k;i++) { Rjep(n) { for(int x=1;x*j<=2000;x++) { dp[i+1][x*j]+=dp[i][j]; dp[i+1][x*j]%=mod; } } } LL ans=0; for(int i=1;i<=n;i++) { ans+=dp[k][i]; ans%=mod; } cout<<ans<<" "; return 0; }