题目链接:
Bear Limak has n colored balls, arranged in one long row. Balls are numbered 1 through n, from left to right. There are n possible colors, also numbered 1 through n. The i-th ball has color ti.
For a fixed interval (set of consecutive elements) of balls we can define a dominant color. It's a color occurring the biggest number of times in the interval. In case of a tie between some colors, the one with the smallest number (index) is chosen as dominant.
There are 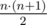 non-empty intervals in total. For each color, your task is to count the number of intervals in which this color is dominant.
non-empty intervals in total. For each color, your task is to count the number of intervals in which this color is dominant.
The first line of the input contains a single integer n (1 ≤ n ≤ 5000) — the number of balls.
line of the input contains a single integer n (1 ≤ n ≤ 5000) — the number of balls.
The second line contains n integers t1, t2, ..., tn (1 ≤ ti ≤ n) where ti is the color of the i-th ball.
Print n integers. The i-th of them should be equal to the number of intervals where i is a dominant color.
4
1 2 1 2
7 3 0 0
3
1 1 1
6 0 0
In the first sample, color 2 is dominant in three intervals:
- An interval [2, 2] contains one ball. This ball's color is 2 so it's clearly a dominant color.
- An interval [4, 4] contains one ball, with color 2 again.
- An interval [2, 4] contains two balls of color 2 and one ball of color 1.
There are 7 more intervals and color 1 is dominant in all of them.
题意:
给出这么多颜色,在一个序列中,dominant是出现次数最多的数,如果出现次数最多的不止一个,那么就是数值最小的那个;
思路:
暴力跑出[i,j]中每个数出现的次数,同时更新这里面的的dominant;
AC代码:
#include <bits/stdc++.h> using namespace std; #define Riep(n) for(int i=1;i<=n;i++) #define Riop(n) for(int i=0;i<n;i++) #define Rjep(n) for(int j=1;j<=n;j++) #define Rjop(n) for(int j=0;j<n;j++) #define mst(ss,b) memset(ss,b,sizeof(ss)); typedef long long LL; const LL mod=1e9+7; const double PI=acos(-1.0); const int inf=0x3f3f3f3f; const int N=1e5+5; int n,flag[5002][5002],a[5002],ans[5002]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); } for(int i=1;i<=n;i++) { int num=0,temp; for(int j=i;j<=n;j++) { flag[i][a[j]]++; if(flag[i][a[j]]>num) { num=flag[i][a[j]]; temp=a[j]; } else if(flag[i][a[j]]==num) { if(a[j]<temp) { temp=a[j]; } } ans[temp]++; } } for(int i=1;i<=n;i++) { printf("%d ",ans[i]); } return 0; }