插入操作
我们可以用类似于二叉搜索树的方法来向树中插入一个元素。它可以在O(lgn)时间内完成,所谓插入就是将新结点插入为叶子节点,从根节点开始遍历。
// 插入 RB_INSERT(T, z) y = T.nil x = T.root while x != T.nil // 找到合适的插入父节点 y = x // y 一定是叶子节点 if z.key < x.key x = x.left else x = x.right z.p = y if y == T.nil // y == T.nil 说明红黑树是空树 T.root = z else if z.key < y.key // 找到合适的位置挂载z y.left = z // 此前 y.left 一定是 T.nil else y.right = z z.left = T.nil // 初始化z节点 z.right = T.nil z.color = RED RB_INSERT_FIXUP(T, z) // 红黑树再平衡
备注:插入操作一定是将z当成一个叶子节点插入
可以看出我们默认把新插入的结点着为红色插入(原因之后给出)。与二叉搜索树的插入算法最为不同的是,
在最后一步我们调用了RB-INSERT-FIXUP方法来维护红黑树的性质。
// 插入再平衡
RB_INSERT_FIXUP(T, z) while z.p.color == RED if z.p == z.p.p.left // 父节点是左孩子 u = z.p.p.right // y是叔叔节点 if u.color == RED z.p.color = BLACK // case1 y.color = BLACK // case1 z.p.p.color = RED // case1 z = z.p.p // case1 else if z == z.p.right z = z.p // case2 LEFT_ROTATE(T, z) // case2 z.p.color = BLACK // case3 z.p.p.color = RED // case3 RIGHT_ROTATE(T, z.p.p) // case3 else // same T.root.color = BLACK
说明:
上述过程可能有些复杂,我们来仔细分析一下,从两个方面入手。
第一,我们应当明确RB_INSERT_FIXUP方法是来维护红黑树的性质的,因此我们要搞清楚插入一个结点(红色)将会打破哪些性质;
第二,我们要具体分析上述的三种情况究竟在做什么、有什么影响。
哪些性质会被破坏
很明显,只有性质①——根结点必须是黑色和性质②——红色结点的孩子必为黑色会被破坏。
三种情况
首先,循环的大前提是z的父结点是红色,父节点是黑色,满足红黑树性质,不需要处理。然后,我们分析的三种情况建立在z的父结点是左孩子基础上(相反情况类似,不做分析)。
我们还容易看出:在每次迭代前,z节点总是红色的;y节点为z节点的“叔叔”(y = z.p.p.right,下面称y为z的叔节点)。
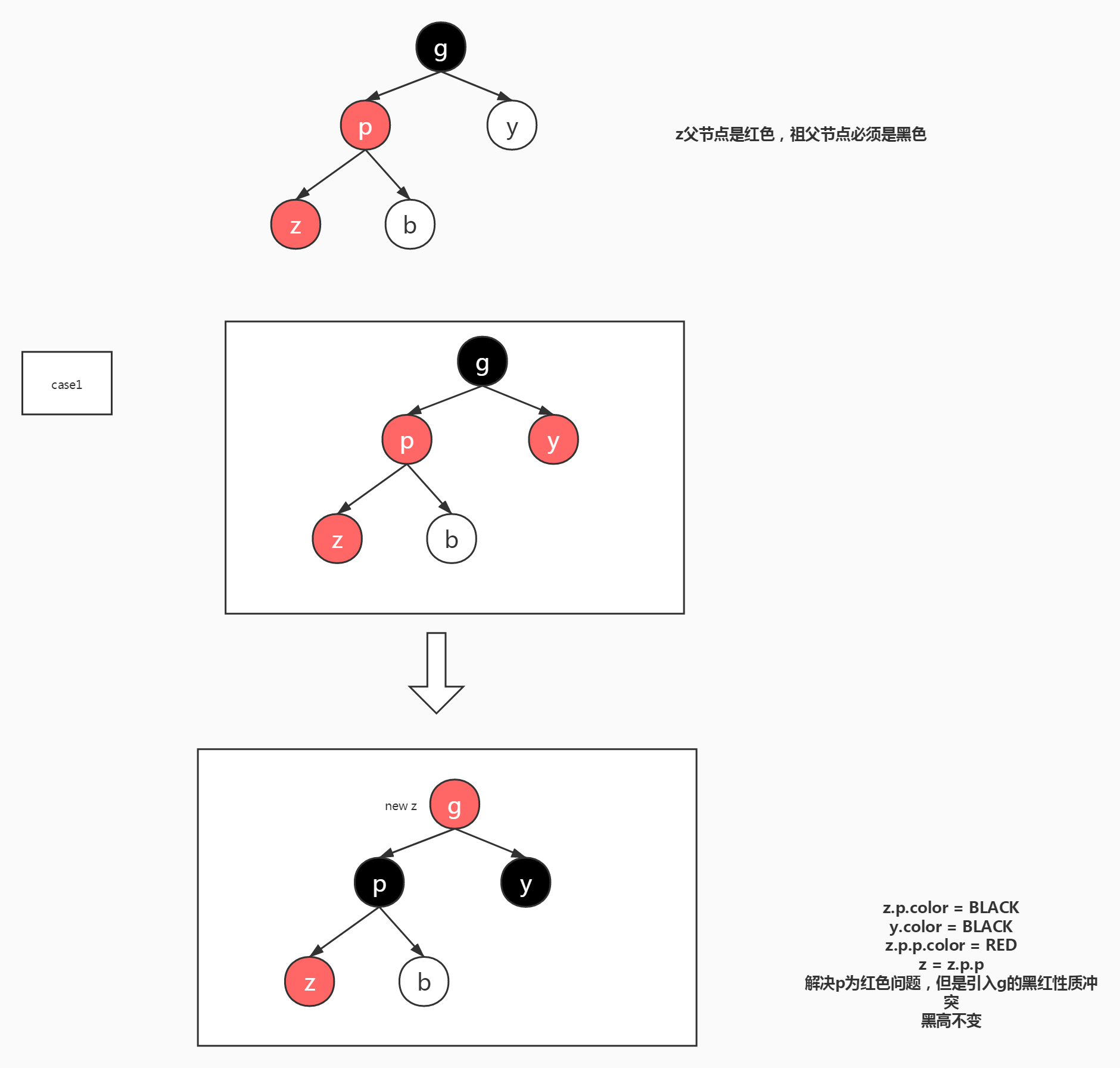
Case 1:z的叔节点y为红色(同时也说明了z的“爷爷”节点是黑色的)。
在做什么:把z的“爷爷”节点着为红色;而把“爷爷”节点的子节点都着为黑色;z上升2级,指向它的“爷爷”节点。
有什么影响:修复了z节点附近的红黑树性质,但是破坏了z爷爷节点附近的红黑树性质,通过z指向爷爷节点,
可以通过循环继续修复z爷爷节点附近的红黑树性质,黑高没有变化
Case 2:z的叔节点y为黑色且z为右孩子。
在做什么:z指向自己的父节点;对z节点进行左旋操作。
有什么影响:为了构造case3的场景,黑高没有变化
Case 3:z的叔节点y为黑色且z为左孩子。
在做什么:把z的父节点置为黑色;把z的“爷爷”节点置为红色;对z的“爷爷”节点进行右旋操作。
有什么影响:修复红黑树的性质,黑高没有任何变化
具体分析如图
/*------------------case2+case3分析-------------------------------------*/

小结:
由于我们默认把新插入的结点置为红色,因此初始时,结点z是红色显然成立。在迭代之前,如果只有一个结点,即只有根结点,性质①被打破;
否则,z和z.p都为红色,性质②被打破;
从上面对三种情况的分析我们可以看出:结点z始终是红色的;三种操作都没有改变任何路径上的黑高,即性质③始终是满足的。
显然每次完成case 1后,性质①或性质②是被打破的。完成case 2一样。当完成case 3后,循环就终止了(因为在case 3中我们把z.p置为了黑色),此时满足红黑性质。
由于一棵有n个结点的红黑树的高度为O(lg n),因此执行RB—INSERT需要O(lg n)时间;在RB-INSERT-FIXUP中,
仅当case 1发生时,while循环才会执行下去;而每次执行完case 1,指针z都会上升2层。
因此while循环最多执行lg n次;所以RB-INSERT-FIXUP时间复杂度为O(lg n),因此整个插入操作的时间复杂度为O(lg n)。