字符串查找和匹配是一个很常用的功能,比如在爬虫,邮件过滤,文本检索和处理方面经常用到。相对与C,python在字符串的查找方面有很多内置的库可以供我们使用,省去了很多代码工作量。但是我们还是需要了解一些常用的字符串查找算法的实现原理。
首先来看python内置的查找方法。查找方法有find,index,rindex,rfind方法。这里只介绍下find方法。find方法返回的是子串出现的首位置。比如下面的这个,返回的是abc在str中的首位置也就是3。如果没找到将会返回-1
str = "dkjabcfkdfjkd198983abcdeefg"
print str.find('abc')
但是在str中有2个abc,那么如何去查找到第二个abc的位置呢。由于find是会返回查找到的字符串的首位置,因此我们可以利用这个位置继续往后搜索。代码如下
def str_search_internal():
str = "dkjabcfkdfjkd198983abcdeefg"
substr='abc'
substr_len=len(substr)
start=0
while start <=len(str):
index=str.find('abc',start)
if index == -1:
return -1
else:
print index
begin=index+substr_len #每一次查找后就将开始查找的位置往后移动字串的长度
if begin <= len(str):
index=str.find('abc',begin)
print index
else:
return -1
start=index+substr_len
通过返回的index方式就可以不断的往下寻找后面匹配的字符串。
前面介绍了python内置的查找函数,那么如果我们不用这些内置的函数,自己如何编写查找函数呢。首先我们来看下朴素的串匹配应用。代码如下
def str_search():
str = "dkjabcfkdfjkd198983abcdeefg"
substr = 'abc'
substr_len = len(substr)
str_len=len(str)
i,j=0,0
while i < str_len and j < substr_len:
if str[i] == substr[j]: #如果匹配,则主串和子串的位置同时后移一位
i+=1
j+=1
else:#如果不匹配,主串移动到当前查找位置的后一位
i=i-j+1
j=0
if j == substr_len: #如果j到了子串的最后一位,表明已经找到匹配的
return i-j
return -1
从代码量的角度来看,直接使用find方法要省事得多。那么从代码的运行时间来看,谁更快呢。来比较下代码的运行时间
start=time.time()
str = "dkjabcfkdfjkd198983abcdeefg"
print str.find('abc')
end=time.time()
print 'the time elapsed %f' % (end-start)
find方法使用的时间为0.000009
/usr/bin/python2.7 /home/zhf/py_prj/data_struct/chapter4.py
3
the time elapsed 0.000009
用朴素的匹配算法运行时间是0.000026,时间是find方法的3倍
start=time.time()
ret=str_search()
print ret
end=time.time()
print 'the time elapsed %f' % (end-start)
/usr/bin/python2.7 /home/zhf/py_prj/data_struct/chapter4.py
3
the time elapsed 0.000026
我们考虑更极端的场景,将主串str初始化为
"dkjueireijkab139u8khbbzkjdfjdiuhfhhionknl90089122jjkdnbdfdfdfddfd981298989dhfjdbfjdbfjdbfjbj"
"djkjdfkdjkfbkadfffffffffffffffffffffffffffffffffffjiiernkenknkdfndkfndkfbdhfkdfjkd198983abcdeefg"
长度更长且abc位于主串的偏后的位置。此时再来比较下两种方式的运行时间。
使用find方法的时间为0.000028
/usr/bin/python2.7 /home/zhf/py_prj/data_struct/chapter4.py
180
the time elapsed 0.000028
使用朴素查找方式的时间为0.000222. 时间增长了将近10倍。因为可以看到字符串的规模越大,使用find方法的时间越少,查找速度越快。
/usr/bin/python2.7 /home/zhf/py_prj/data_struct/chapter4.py
180
the time elapsed 0.000222
通过对比可以发现朴素查找算法的效率很低,原因在于执行的过程在不断的回溯,匹配中遇到字符不同的时候,主串str将右移一个字符位置,随后的匹配回到子串substr的开始继续开始匹配。这种方式完全没有利用之前查找得到的信息来进行下一步的判断,可以认为是一种暴力搜索。假设有如下的场景主串是000000000000000000001。子串是001。而001位于最后3位。按照朴素查找方法,这个算法的复杂性为O(m*n).
由于朴素查找算法的效率太低,因此来看下一种查找效率更高的算法:KMP算法。
比如abc这个串找它在abababbcabcac这个串中第一次出现的位置,那么如果直接暴力双重循环的话,abc的c不匹配主串中的第三个字母a后,abc将开始从母串中的头位置的下一个位置开始寻找,就是abc开始匹配主串中第二个字母bab...这样。但是其实在主串中能够匹配的字母应该是a开始的,因此abc去匹配bab一开始也是不匹配的。这样多出了一次无谓的匹配。效率更高的方法就是用abc去匹配主串中的第三个字母aba
而KMP的优势就在于可以让模式串向右滑动尽可能多的距离就是abc直接从模式串的第三个字母aba...开始匹配,为了实现这一目标,KMP需要预处理出模式串的移位跳转next数组。
我们来用一个实际的例子来看下该如何优化
1 下面的例子在子串和主串比较到D的时候发现不一致了

按照朴素的搜索算法,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍

当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。如下图,因为有相同的AB存在,因此直接移动AB的位置进行比较
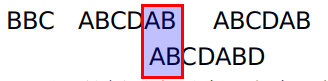
下面来介绍kmp算法的思想。
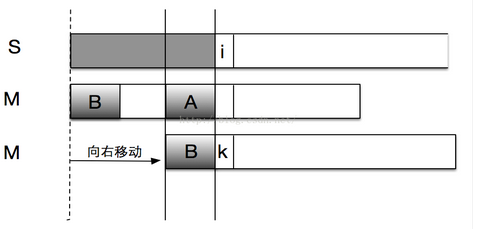
在字符串S中寻找M,假设匹配到位置i时两个字符才出现不相等(i位置前的字符都相等),这时我们需要将字符串M向右移动。常规方法是每次向右移动一位,但是它没有考虑前i-1位已经比较过这个事实,所以效率不高。事实上,如果我们提前计算某些信息,就有可能一次右移多位。假设我们根据已经获得的信息知道可以右移x位,我们分析移位前后的M的特点,可以得到如下的结论:
B段字符串是M的一个前缀
A段字符串是M的一个后缀
A段字符串和B段字符串相等
所以右移x位之后,使M[k] 与 S[i] 对齐,继续从i位置进行比较的前提是:M的前缀B和后缀A相同。
这样就可以得出KMP算法的核心思想:
KMP算法的核心即是计算字符串M每一个位置之前的字符串的前缀和后缀公共部分的最大长度。获得M每一个位置的最大公共长度之后,就可以利用该最大公共长度快速和字符串S比较。当每次比较到两个字符串的字符不同时,我们就可以根据最大公共长度将字符串M向右移动,接着继续比较下一个位置。
所以KMP就需要找出前缀和后缀的最大长度并记录下来,也就是我们用到的next数组。
这里需要对前缀和后缀的意义进行解释下
"前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。举个例子来说明下,比如字符串ABCDABD
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0
对于目标字符串ptr,ababaca,长度是7,所以next[0],next[1],next[2],next[3],next[4],next[5],next[6]分别计算的是
a,ab,aba,abab,ababa,ababac,ababaca的相同的最长前缀和最长后缀的长度.所以next数组的值是[-1,-1,0,1,2,-1,0],这里-1表示不存在,0表示存在长度为0,2表示存在长度为2
为方便起见,next数组下标都从1开始,M数组下标依然从0开始
假设我们现在已经求得next[1]、next[2]、……next[i],分别表示不同长度子串的前缀和后缀最大公共长度,下面介绍如何用归纳法计算next[i+1] ?
假设k=next[i],它表示M位置i之前的字符串的前缀和后缀最大公共长度,即M[0...k-1] = M[i-k...i-1];
比如假设子串为如下。
a b c e r e j k a b c k
0 1 2 3 4 5 6 7 8 9 10 11
那么next[11]=3。M[0-2]=M[11-3..11-1]=M[8,10]。这个就表示位置11之前的字符串的前缀和后缀的最大公共长度为3
接下来看下如何求出next数组. k表示前缀数据,i表示后缀数据
(1)若M[k] = M[i]相等, 则必定有next[i+1] = next[i] +1,即M位置i+1之前的字符串的前缀和后缀最大公共长度为k+1。还是按照上面的字符串为例M[2]=M[10], next[11]=3,next[10]=2, 因此next[i+1]=next[i]+1
(2)若M[k] != M[i], 则 k索引next[k]直到与p[j]相等或者前缀子符串长度为0,此时可用公式next[j+1]=k+1
归纳一下:令 next[k] = j, 继续判断M[i] 与 M[j] 是否相等,如果相等则 next[i+1] = next[k] + 1 = next[ next[i] ] + 1;如果不相等重复步骤(2),继续分割长度为next[ next[k] ]的字符串,直到字符串长度为0为止
那么为了实现这种生成关系,我们需要设定一个标量,设定k的前缀初始值为-1。next数组全部也初始为-1。我们还是以这个字符串为例.j=0
a b c e r e j k a b c k
0 1 2 3 4 5 6 7 8 9 10 11
1 next[0]:从第一个字母开始,没有可对比前缀和后缀,因此等于-1.这里我们用-1这个标量也是为了表示没有找到匹配的前缀和后缀. j=0 k=-1
2 next[1]: 求ab的最大公共长度,由于k=-1,没有可匹配的前缀。因此next[1]=0, j=1,k=0
3 next[2]: 求abc的最大公共长度,此时P[1]!=P[0], 继续向前最小子串查找k=next[k=0]=-1没有找到可匹配的前缀,因此next[2]=0 j=2,k=0
4 next[3]: 求abce的最大公共长度。由于p[2]!=p[0], 因此继续往前缀查找。也就是k=next[k]=next[0]=-1. 由于k=-1没有找到可匹配的前缀,因此next[3]=0. 变量j=3,k=0
.
.
.
.
.
5 next[9],求abcerejkab的最大公共长度. p[8]=p[0]。因此next[9]=next[8]+1=0+1=1 j=9,k=1
6 next[10],求abcerejkabc的最大公共长度. p[9]=p[1]。因此next[10]=next[9]+1=1+1=2 变量:j=10,k=2
7 next[11],求abcerejkabck的最大公共长度. p[10]=p[2]。因此next[10]=next[9]+1=2+1=3 变量:j=11,k=3
根据前面的描述就可以得出我们的代码实现
def get_next(substring):
lenth=len(substring)
next_table=[-1]*lenth
k=-1
j=0
while j < lenth-1:
#substring[j]表示后缀,substring[k]表示前缀
if k==-1 or substring[j]==substring[k]:
j+=1
k+=1
next_table[j]=k
print j,k,next_table
#没有找到匹配的,继续往前最小子串进行查找
else:
k=next_table[k]
return next_table
因此可以得到next表如下:
[-1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 3]
既然next表已经得到,我们就可以写出对应的KMP算法实现了
def kmp_function(str,substring):
len1=len(str)
len2=len(substring)
next_table=get_next(substring)
print next_table
k=-1
i=0
while i < len1:
while(k>-1 and substring[k+1] != str[i]):
k=next_table[k]
if substring[k+1] == str[i]:
k=k+1
if k==len2-1:
return i-len2+1
i+=1
从这个实现可以看出KMP的实现复杂度为O(m+n),比朴素的查找算法的O(m*n)提高了不少.那么我们继续分析下KMP算法是否有优化的空间呢. 来看下面的例子:
如果用之前的next 数组方法求模式串“abab”的next 数组,可得其next 数组为-1 0 0 1(0 0 1 2整体右移一位,初值赋为-1),当它跟下图中的文本串去匹配的时候,发现b跟c失配,于是模式串右移j - next[j] = 3 - 1 =2位。

右移2位后,b又跟c失配。事实上,因为在上一步的匹配中,已经得知p[3] = b,与s[3] = c失配,而右移两位之后,让p[ next[3] ] = p[1] = b 再跟s[3]匹配时,必然失配。问题出在哪呢?

问题出在不该出现p[j] = p[ next[j] ]。为什么呢?理由是:当p[j] != s[i] 时,下次匹配必然是p[ next [j]] 跟s[i]匹配,如果p[j] = p[ next[j] ],必然导致后一步匹配失败(因为p[j]已经跟s[i]失配,然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配,很显然,必然失配),所以不能允许p[j] = p[ next[j] ]。如果出现了p[j] = p[ next[j] ]咋办呢?如果出现了,则需要再次递归,即令next[j] = next[ next[j] ]。总结即是:
如果a位字符与它的next值(即next[a])指向的b位字符相等(即p[a] == p[next[a]]),则a位的next值就指向b位的next值即(next[ next[a] ])。
那么代码修改如下就可以了:
def get_next(substring):
lenth=len(substring)
next_table=[-1]*lenth
k=-1
j=0
while j < lenth-1:
if k==-1 or substring[j]==substring[k]:
j+=1
k+=1
#如果p[j]==p[next[j]],则继续递归,直到p[j]!=p[next[j]]
if substring[j] == substring[k]:
next_table[j]=next_table[k]
else:
next_table=k
else:
k=next_table[k]
return next_table