@
因为一本通少了一些算法,所以我就自行补充了一些东西上去。
EXKMP也就是扩展KMP,是一种特别毒瘤的东西
EXKMP确实很难,我理解他的时间与AC机的时间差不多,而且还很难记,因此一学会就马上写博客了QAQ
定义
EXKMP就是解决这种问题的。
先讲两个数组的定义(默认所有数组从1开始):
ex数组,代表A(主串)的从第i位与B(子串)的最长相同前缀。
next数组,代表B(子串)的从第i位与B(子串)的最长相同前缀。
算法思想
注:所有字符串下标从1开始
首先,假定已经匹配的ex数组位置为1~a,next数组全部匹配好了(next数组的匹配方式跟ex数组的匹配方式大致相同,后面会讲,不用担心)。
首先,我们定义一个(p),代表(max(i+ex_{i}-1)(iin [1,a])),也就是目前在主串中匹配到的最远的位置,同时设能使p最大的(i)为(b),设目前要匹配(k)的位置。
首先,我们知道,当(a<=p)时,那么我们可以知道(A_{b ightarrow p}=B_{1 ightarrow (p-a+1)})。
注:至于(a==p+1)的情况仅当(ex_{a}=0)并且以前的(i+ex_{i}-1)都没有超过(a-1),且在这种情况下,在后面会讲到,将被归类在(k+L>=p)中(k>p)的情况,不会造成任何任何影响,后面会讲,无需着急,同时不会有(a>p-1)的情况。
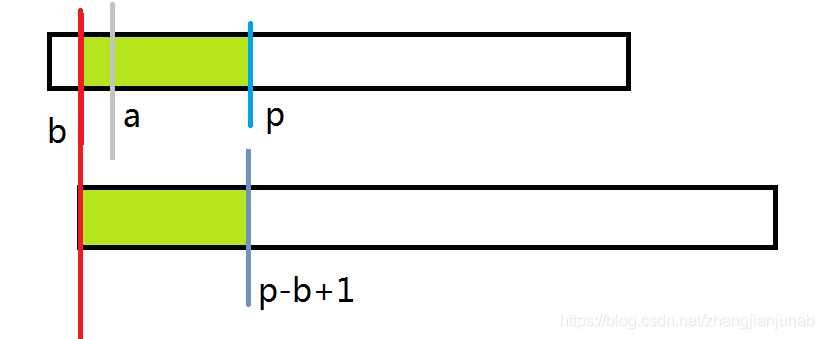
注:上面是B串,下面是A串,绿色部分为相等部分。
那么,我们去掉一起从开头去掉(k-b)长度的字符串,即为(A_{k ightarrow p}=B_{(k-b+1) ightarrow (p-a+1)})(紫色部分)
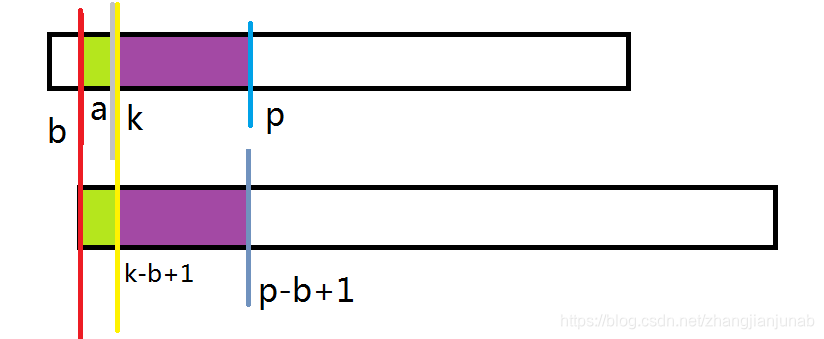
注:为什么(k)挨着(a)?因为(k=a+1),这里为证明方便,多设一个k。
但是,我们并不知道从A串从(k)开始的地方与B串从(1)开始的地方有什么瓜葛?
这时候,我们需要一员大将:设(L=next_{k-b+1}),没错,我们知道了(A_{k ightarrow p}=B_{(k-b+1) ightarrow (p-a+1)}),那么我们就可以找出从(B_{1})开始最长可以与(B_{(k-b+1)})相等多少,就是next数组。
这时候,有了两种情况:
先设(now=k+L-1)。
- now<p
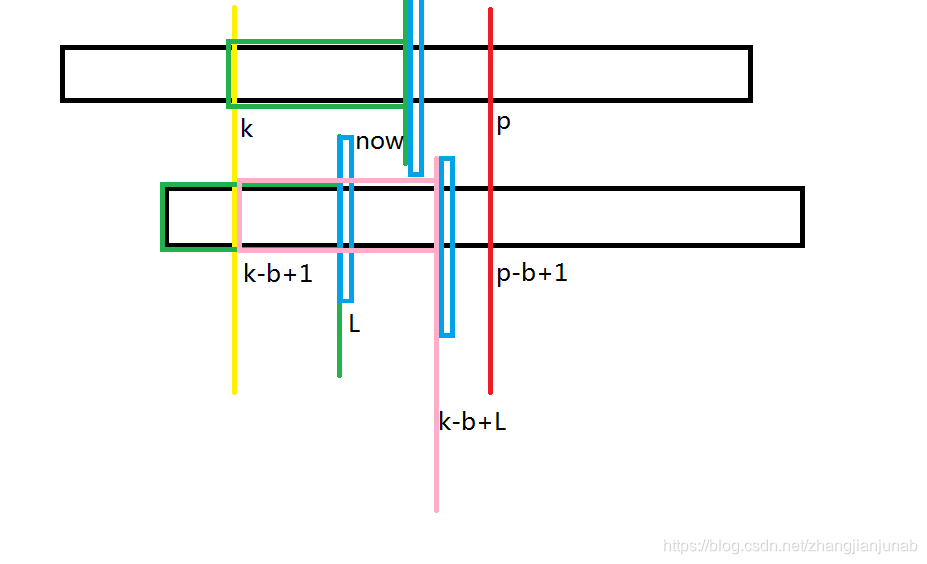
注:上面是B串,下面是A串,粉色框框与绿色框框为相等部分。
我们发现,三个蓝色部分:(B_{(now+1)},A_{(L+1)},A_{(k-b+L+1)}),根据前面,我们知道:(B_{(now+1)}=A_{(k-b+L+1)}),有根据next数组的定义,我们知道(A_{(L+1)} e A_{(k-b+L+1)})(如果不是的话,L可以++),那么,我们可以知道(A_{(L+1)} e B_{(now+1)}),所以,这个时候(ex_{k}=L)。
- now>p
这也分两种情况:
- k>p
这个时候应当从(k)开始暴力匹配,因为(k)不在(p)的范围内,(k-b+1)也不在(p-b+1)的范围内,所以只能暴力匹配。

2.k≤p
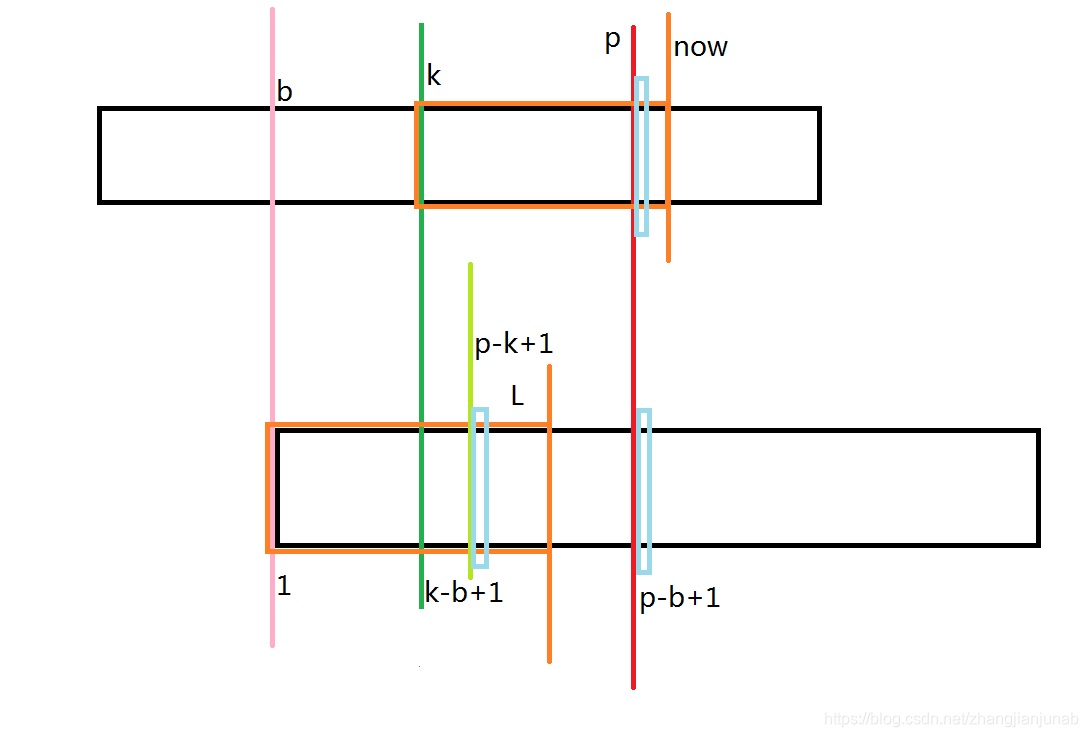
首先,我们知道now>p,意味着什么?你真的学会的话,应该知道如果now>p,那么(k-b+1+L-1=k-b+L>(p-b+1))。
那么,这里面的(p-k+1)其实就是在(B_{1})至(B_{L})中与(B_{p-b+1})所对应的位置,也就是与(A_{p})所对应的位置。
那么我们就知道了三个关键位置(A_{p},B_{p-k+1},B_{p-b+1}),我们看他后面的浅蓝色框框框住的位置(A_{p+1},B_{p-k+2},B_{p-b+2}),像上一个那么推:(A_{p+1} e B_{p-b+2},B_{p-b+2}=B_{p-k+2}),那么,我们就可以知道(A_{p+1} e B_{p-k+2}),那么,这个时候我们就可以知道这时候(ex_{k}=p-k+1)
- now=p
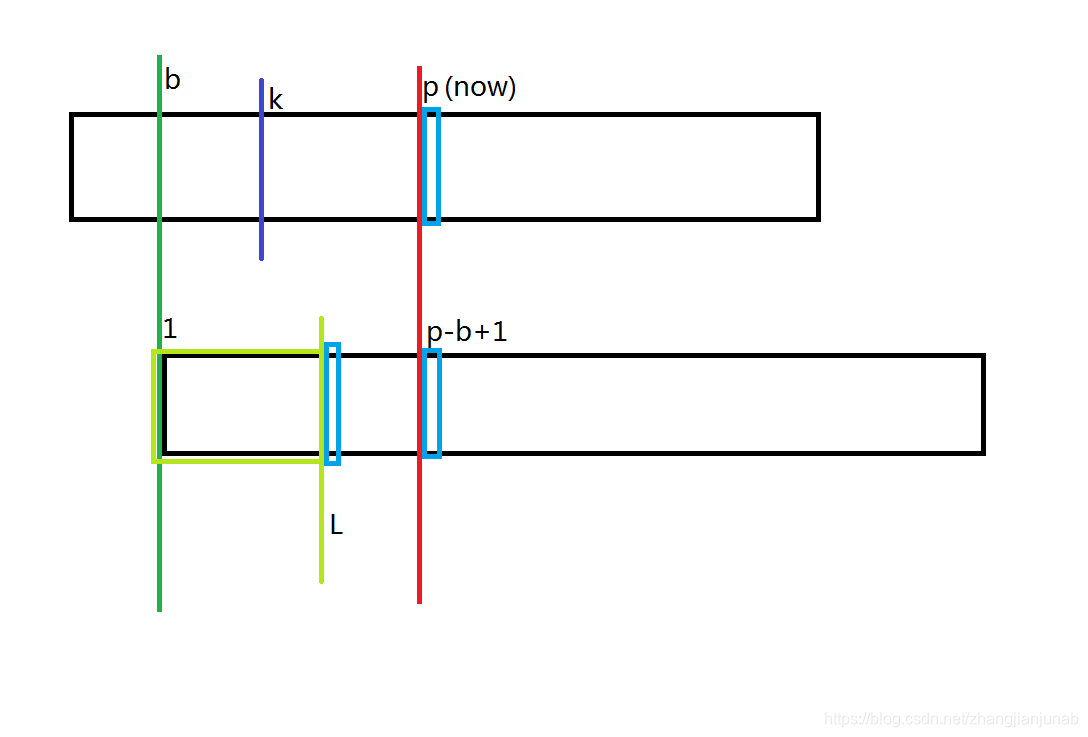
这种情况下,由于(now==p),所以导致在(B_{(p+1)},A_{(L+1)},A_{(p-b+2)})中,(B_{(now+1)} e A_{(p-b+2)}),根据next数组的定义,我们知道(A_{(L+1)} e A_{(p-b+2)})(如果不是的话,L可以++),但是(A_{(p+1)} e B_{(L+1)})是不一定的。如(a e b,b e a,a=b)
那么,我们就直接等于p,然后不断暴力匹配,然后更新(b)、(p)、(a)。(其实(a)根本不需要记录的)
至于next如何匹配,就把B当成子串与主串就行了,不过(next_{1})可以不用去理他。。。
复杂度:每个数匹配一次,(p)最多向右移到(n)(母串)。
当然,代码上有些细节,大家需要自行推倒一下:
#include<cstdio>
#include<cstring>
#define N 1100000
using namespace std;
int next[N],ex[1100000],n,m;
char A[N],B[N];
inline int mymin(int x,int y){return x<y?x:y;}
void exkmp()
{
//匹配next数组,由于next数组都为0,可以一开始不预处理出ex[2]。
int b=0,p=0;
for(int i=2;i<=m;i++)
{
int L=next[i-b+1]/*i-b+1>1*/,now=i+L-1/*判断用的变量*/;
if(now<p)next[i]=L;
else//包括情况二与情况三
{
int pp=p-i+1<0?0:p-i+1;
while(i+pp<=m/*因为i+pp>pp+1(pp≥2),所以判断i+pp就行了*/ && B[i+pp]==B[pp+1])pp++;
next[i]=pp;b=i;p=next[b]+b-1;//更新
}
}
b=p=0;//不用担心,他会跳到else里面去的
for(int i=1;i<=n;i++)
{
int L=next[i-b+1],now=i+L-1;
if(now<p)ex[i]=L;
else
{
int pp=p-i+1<0?0:p-i+1;
while(i+pp<=n && pp<m && A[i+pp]==B[pp+1])pp++;
ex[i]=pp;b=i;p=b+ex[b]-1;
}
}
}
int main()
{
scanf("%s%s",A+1,B+1);n=strlen(A+1);m=strlen(B+1);//输入
exkmp();//匹配
for(int i=1;i<n;i++)printf("%d ",ex[i]);//输出
printf("%d
",ex[n]);
return 0;
}
疑难杂症
没错,EXKMP就是这么难,于是我写了疑难杂症。其实就是自己太弱了,所以需要写。。。
1
代码中怎么只有情况一与情况三的代码?
因为我们发现情况二的代码可以在情况三的代码里面。
2
为什么不用预处理出(ex)数组与(next)数组的一个数字来更新(b)与(p)?
因为在一开始中,我们(b=p=0)
那么(i+L-1)就算(i=1,L=0),(i+L-1)也大于(1),所以我们可以放心的交给for循环。
3
困扰了我一段时间的一个问题,解决后发现是我想错方向,同时又想的太复杂的。
就是,当(b)与(p)更新了,在求原来的(b-p)与现在的(b-p)的交集的地方的时候,我们在求(ex)或(next)数组时,(i-b+1)是不同的,现在的(b)大于原来的(b),那么现在的(i-b+1)就小于原来的(i-b+1),是否会影响结果?

其实并不然,简单点,佛系思想:因为方法正确,只要是合法的(b,p),都可以求出(ex_{i})或(next_{i})。
但是,深入一点想,更新了(b)与(p),会不会影响求两个地方交集部分的(ex)或(next)?
画图帮助理解:
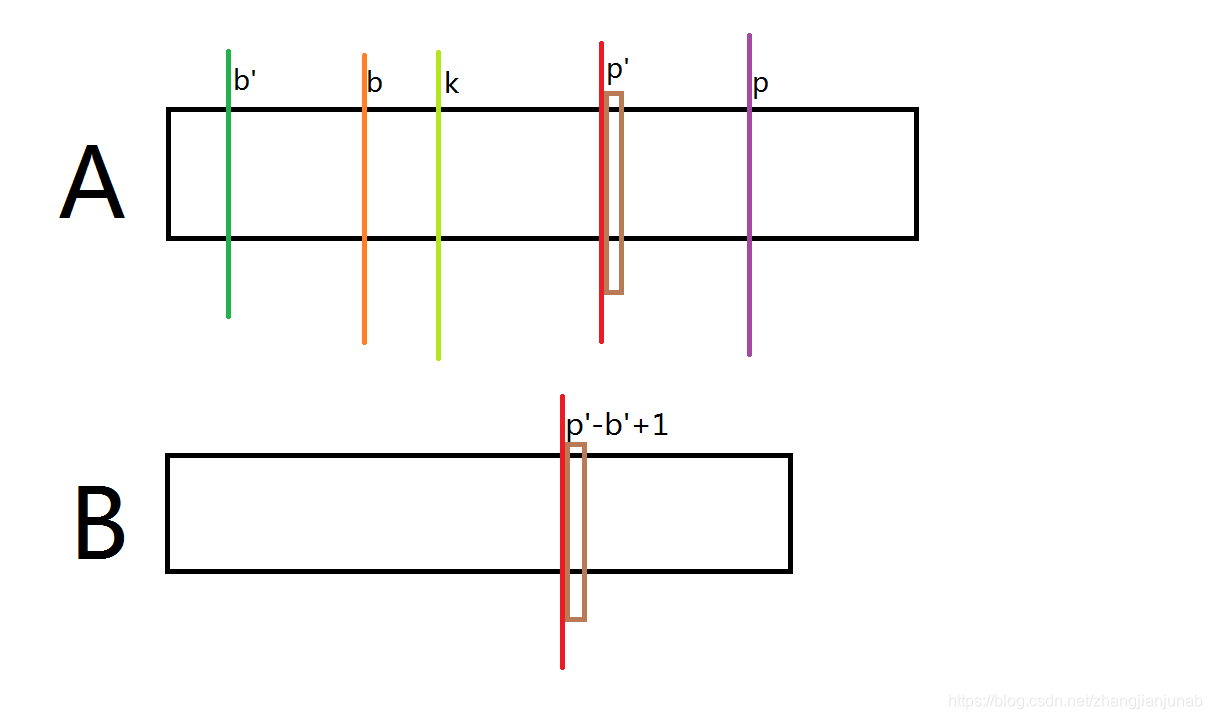
首先,棕色格子不相等,我们是知道的。
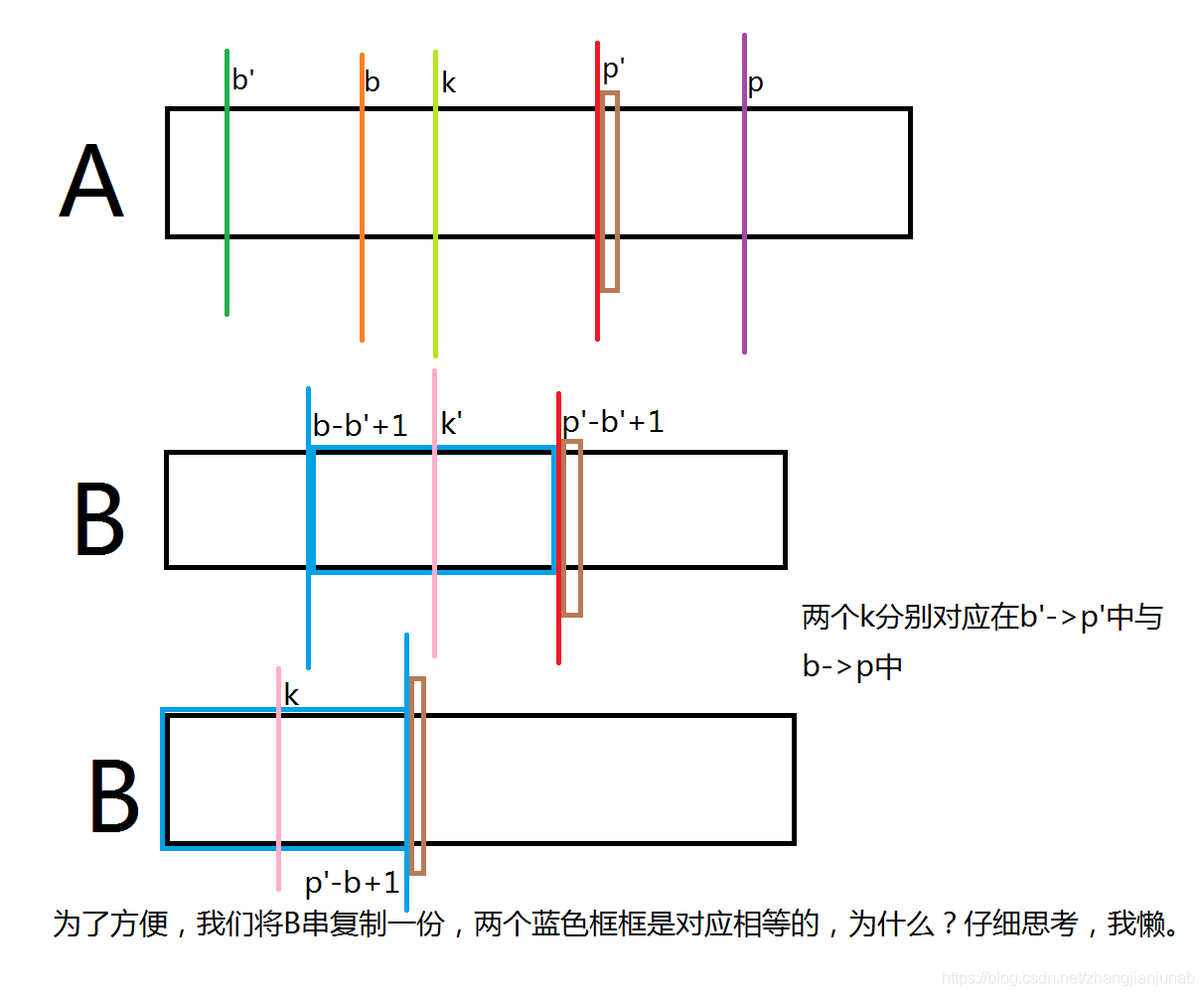
分三种情况考虑:
- (next_{k'}+k'-1<p'-b'+1)
这个时候,因为两个蓝色框框对应相等,所以(next_{k}=next_{k'})。
2.(next_{k'}+k'-1=p'-b'+1)
这个时候,我们知道(B_{p'-b'+2} e B_{next_{k'}+1}),又因为(B_{p'-b'+2} e B_{p'-b+2}),那么,我们还是不知道(B_{next_{k'}+1},B_{p'-b+2})的关系。。。那么(k'+next_{k}+1≥p'-b'+1)。
这种情况下匹配是否相等?
首先(next_{k'}+k'-1=p'-b'+1),那么,在(b',p')的情况下,(k)会去暴力匹配,那么在(b',p')的情况下,看(next_{k})的情况,反正(next_{k}≥next_{k'}),至少不会错,反而快了。
- (next_{k}+k'-1=p'-b'+1)
照样像上面证明,得到(next_{k'}+k'-1≥p'-b'+1),那么,我们知道(p'≥p),首先(next_{k}+k'-1=p'-b'+1),那么我们知道这时候(now≤p),那么,在(b,p)中,最多暴力匹配或者跳到情况得到(匹配中的情况1,不是这里的情况1),而(next_{k'}+k'-1≥p'-b'+1),那么,在(b',p')中,(k)在A中的ex值也就是(p'-k+1),可是在(b,p)中还有个暴力匹配的情况?
想想就知道,暴力匹配不会得出什么新的答案,最后结果还是(p'-k+1)
至此,问题3解决,完结撒花。
大家有什么问题可以在评论区问我。
练习题目
双倍经验
哈哈哈,双倍经验。
作为一道练手题目看待吧。
#include<cstdio>
#include<cstring>
#define N 1100000
using namespace std;
int next[N],ex[1100000],n,m;
char A[N],B[N];
inline int mymin(int x,int y){return x<y?x:y;}
void exkmp()
{
//匹配next数组,由于next数组都为0,可以一开始不预处理出ex[2]。
int b=0,p=0;
for(int i=2;i<=m;i++)
{
int L=next[i-b+1]/*i-b+1>1*/,now=i+L-1/*判断用的变量*/;
if(now<p)next[i]=L;
else
{
int pp=p-i+1<0?0:p-i+1;//代表目前从i位置已经匹配的长度。
//里面有特判情况2中的情况2.
while(i+pp<=m/*因为i+pp>pp+1(pp≥2),所以判断i+pp就行了*/ && B[i+pp]==B[pp+1])pp++;
next[i]=pp;b=i;p=next[b]+b-1;//更新
}
}
//因为next数组匹配完了,要先处理出ex[1]
b=p=0;//会跳到情况二
//更匹配next差不多的代码
for(int i=1;i<=n;i++)
{
int L=next[i-b+1],now=i+L-1;
if(now<p)ex[i]=L;
else
{
int pp=p-i+1<0?0:p-i+1;
while(i+pp<=n && pp<m && A[i+pp]==B[pp+1])pp++;
ex[i]=pp;b=i;p=b+ex[b]-1;
}
}
}
int main()
{
scanf("%s%s",A+1,B+1);n=strlen(A+1);m=strlen(B+1);//输入
exkmp();//匹配
for(int i=1;i<n;i++)printf("%d ",ex[i]);//输出
printf("%d
",ex[n]);
return 0;
}
应用
这道题目其实可以用Manacher来做的,但是毕竟标签是EXKMP,就用EXKMP来做。
首先,我们设(A')是(A)倒过来的串,那么分别把(A')与(A)当成主串或子串处理出两个ex数组。
至此,打架应该大概有思路了吧。
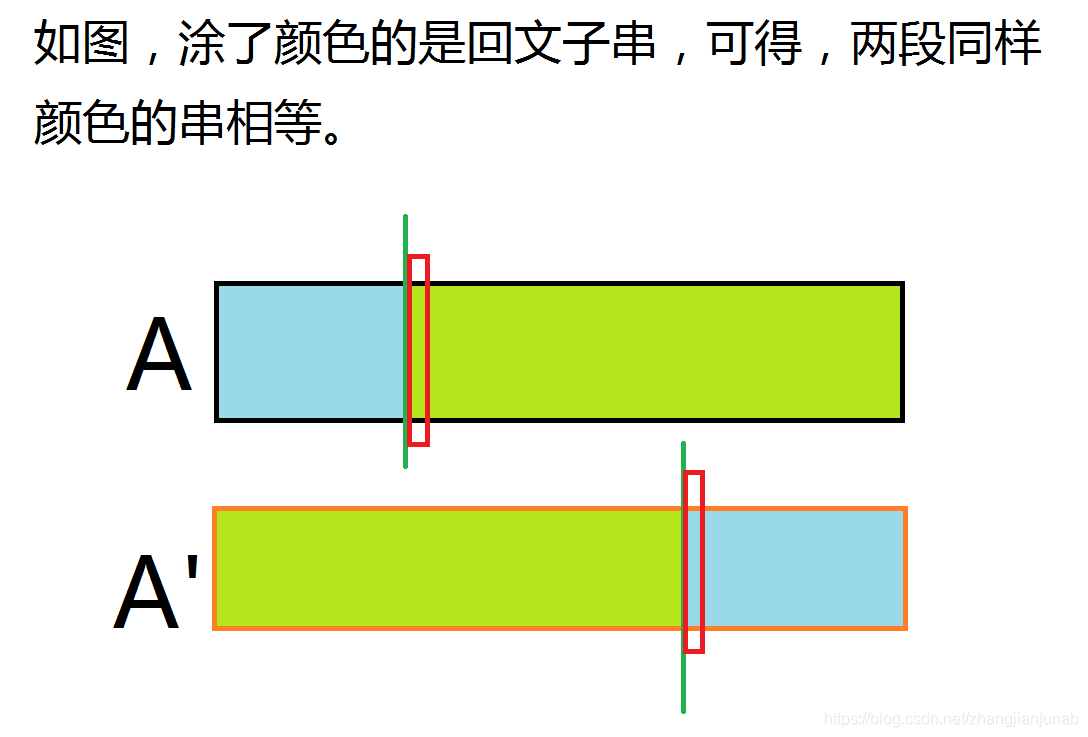
两个红色格子圈住的是重点,看(A')串,假设(A)与(A')的长度为(n),蓝色部分长度为(i),那么,我们可以看以(A'_{(n-i+1)})为开头的前缀,与(A)串以(A_{1})开头的那个前缀相等,且要求求出最长的长度。
仔细一看,不就是ex数组的定义?那么,我们可以由(ex2_{(n-i+1)})得出,(ex2是以(A)为子串,(A')主串的ex数组),那么我们仔细观察发现,当(ex2_{(n-i+1)}≥(i/2))时,(A)中([1,i])的子串就是一个回文子串。
至于如何判断([i+1,n])的子串是否是回文子串,建议自己想,当然,图片中(A)串上也有一个红色框框框住的格子,方法与上面相同,也就不再赘述。作者越来越懒了。。。
#include<cstdio>
#include<cstring>
#define N 510000
using namespace std;
char st1[N],st2[N];
int ex1[N],ex2[N],next[N],n;
inline int mymin(int x,int y){return x<y?x:y;}
inline int mymax(int x,int y){return x>y?x:y;}
void exkmp(char A[]/*母串*/,char B[]/*母串*/,int ex[]/*ex数组*/)//一遍exkmp
{
//next
int b=0,p=0;
for(int i=2;i<=n;i++)//处理next
{
int L=next[i-b+1],now=i+L-1;
if(now<p)next[i]=L;
else
{
int qq=p-i+1<0?0:p-i+1;
while(i+qq<=n && B[i+qq]==B[qq+1])qq++;
next[i]=qq;b=i;p=next[b]+b-1;
}
}
//ex
b=p=0;
for(int i=1;i<=n;i++)//处理ex
{
int L=next[i-b+1],now=i+L-1;
if(now<p)ex[i]=L;
else
{
int qq=p-i+1<0?0:p-i+1;
while(i+qq<=n && A[i+qq]==B[qq+1])qq++;
ex[i]=qq;b=i;p=ex[b]+b-1;
}
}
}
int d[30],sum[N];//处理权值和
int main()
{
int T;scanf("%d",&T);
while(T--)
{
for(int i=1;i<=26;i++)scanf("%d",&d[i]);
scanf("%s",st1+1);n=strlen(st1+1);
for(int i=1;i<=n;i++)st2[i]=st1[n-i+1],sum[i]=sum[i-1]+d[st1[i]-'a'+1];//倒着的串
exkmp(st1,st2,ex1);exkmp(st2,st1,ex2);//处理正着跟倒着
int ans=0;
for(int i=1;i<n;i++)//暴力处理最大值
{
int now=0;
if(ex2[n-i+1]>=i/2)now+=sum[i];//判断[1,i]是否是回文串
if(ex1[i+1]>=(n-i)/2)now+=sum[n]-sum[i];//判断[i+1,n]是否是回文串
ans=mymax(ans,now);//更新
}
printf("%d
",ans);
}
return 0;
}
这道题目,嗯,十分牛逼,用kmp可以解决,但是时间是EXKMP的两倍。
EXKMP怎么做?
先看做法:
定义E的最大长度为(maxlen=max(min(i,next_{i},(n-i)/2))(1≤i≤n)),然后在(1)到(n-1)的区间内找一个数字(i),使得(next_{i})最大,且(next_{i}≤maxlen)与(next_{i}+i-1=n)。
正确性:
我们知道,现在E的长度最长为maxlen(至于为什么,需要读者去深刻理解),(maxlen)的作用实际上就是规定了开头的E与中间的E的存在,为寻找最后的E做下铺垫。
(maxlen)是怎样的?
(min(i,next_{i},(n-i)/2)))实际上是规定了中间的E从(i)开始长度最长是多少,中间的(next_{i})就规定了中间的E与开头的E相对成立,在相对成立的情况下,又不能超过(min(i,(n-i)/2)))。
那么找到了一个(next_{i}(next_{i}+i-1=n) && (next_{i}≤maxlen))时,首先(next_{i}+i-1=n),这规定开头的E与结尾的E,然后(next_{i}≤maxlen),说明这个E的长度没有超过最大的E的限制,将中间的E也规定了,所以这种方法是成立的。
优化:
我们在找(next_{i})的时候,我们可以发现只有在((2/3)n)到(n-1)里面找才会找到合法的(next_{i})。
我知道我讲的不是很好
Code
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 1100000
using namespace std;
int ne[N],n;
char st[N];
void exnext()
{//匹配next数组
int b=0,p=0;
for(int i=2;i<=n;i++)
{
int L=ne[i-b+1],now=i+L-1;
if(now<p)ne[i]=L;
else
{
int qq=p-i+1<0?0:p-i+1;
while(i+qq<=n && st[qq+1]==st[i+qq])qq++;
ne[i]=qq;b=i;p=ne[b]+b-1;
}
}
}
inline int mymin(int x,int y){return x<y?x:y;}//最小值
inline int mymax(int x,int y){return x>y?x:y;}//最大值
int main()
{
int T;scanf("%d",&T);
while(T--)
{
scanf("%s",st+1);n=strlen(st+1);
exnext();
int max_len=0;
for(int i=1;i<=n;i++)
{
int now=mymin(mymin(i,ne[i]),(n-i)/2);
max_len=mymax(max_len,now);
}//处理maxlen
int edd=(n*2)/3,ans=0;
for(int i=edd;i<=n;i++)//找next[i]
{
if(ne[i]>max_len)continue;//不满足条件
if(i+ne[i]-1==n)//满足条件
{
ans=ne[i];//最大的ne
break;//退出
}
}
printf("%d
",ans);//输出
}
return 0;
}
这道题可以用kmp做,等会说,但是我们讲exkmp的做法。
首先,找到一个长度最短的字符串,一次枚举他的每个后缀与每个字符串匹配到的最小长度,然后取每个前缀得到的值的最大值就行了。
KMP就是枚举前缀,而EXKMP枚举后缀。。。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#define N 210
using namespace std;
inline int mymin(int x,int y){return x<y?x:y;}
inline int mymax(int x,int y){return x>y?x:y;}
int ex[N],ne[N]/*就是原本的next数组*/,n,m;
char st[4100][N];
void exnext(char yy[])//匹配出next数组
{
m=strlen(yy+1);
int b=0,p=0;
for(int i=2;i<=m;i++)
{
int L=ne[i-b+1],now=i+L-1;
if(now<p)ne[i]=L;
else
{
int qq=p-i+1<0?0:p-i+1;
while(i+qq<=m && yy[i+qq]==yy[qq+1])qq++;
ne[i]=qq;b=i;p=ne[b]+b-1;
}
}
}
int exkmp(char xx[],char yy[])//匹配ne数组
{
n=strlen(xx+1);//这里不用更新m的原因是在exnext中就更新了m了。
int b=0,p=0,maxid=0;
for(int i=1;i<=n;i++)
{
int L=ne[i-b+1],now=i+L-1;
if(now<p)ex[i]=L;
else
{
int qq=p-i+1<0?0:p-i+1;
while(i+qq<=n && qq<m && xx[i+qq]==yy[qq+1])qq++;
ex[i]=qq;b=i;p=ex[b]+b-1;maxid=mymax(maxid,ex[i]);//记录与这个字符串的最大匹配值
}
}
return maxid;//返回
}
int main()
{
int T,minlen,mind;scanf("%d",&T);
while(T)//多组数据
{
minlen=0;mind=999999999;
for(int i=1;i<=T;i++)
{
scanf("%s",st[i]+1);
if(strlen(st[i]+1)<mind)mind=strlen(st[i]+1),minlen=i;
}//找最短的字符串
int ans=0,weizhi=0;
for(int i=1;i<=mind;i++)
{
int now=999999999;//记录最小的匹配值
exnext(st[minlen]+i-1);//先处理next
for(int j=1;j<=T;j++)//找到最小的匹配数
{
if(j!=minlen)
{
int ttk=exkmp(st[j],st[minlen]+i-1);
if(ttk<now)now=ttk;
}
}
if(now==ans)//一样的长度?找到最小字典序。
{
for(int j=1;j<=ans;j++)
{
if(st[minlen][weizhi+j-1]<st[minlen][i+j-1])break;
else if(st[minlen][weizhi+j-1]>st[minlen][i+j-1]){weizhi=i;break;}
}
}
else if(now>ans)weizhi=i,ans=now;//最大长度,更新
}
if(ans==0)printf("IDENTITY LOST
");//什么都没匹配到
else
{
for(int i=1;i<=ans;i++)printf("%c",st[minlen][weizhi+i-1]);//输出
printf("
");
}
scanf("%d",&T);//输入
}
return 0;
}
小结
今天终于学会了EXKMP了,先撒一波花。
另外,在码代码的时候需要注意几点:
- 在不加特判的情况下,(i-now)有可能大于(1)的。
- 一开始处理(next[2])和(ex[1])的时候需要注意。
把这几点注意了,基本上你爱怎么打怎么打了。
(:光速逃