【算法】素数专题（素数个数表）

【素数判定】

假设输入的都是正数，时间复杂度O（sqrt（n））

bool is_prime(int n){
    for(int i = 2;i*i <= n; i++){
        if(n % i == 0) return false;
    }
    return n != 1;
} 

【因数枚举】

时间复杂度O（sqrt（n））.

vector<int> divisor(int n){
    vector<int> res;
    for(int i = 1;i*i <= n; i++){
        if(n % i == 0){
            res.push_back(i);
            if(i != n/i) res.push_back(n / i);
        }
    }
}

【质因数分解】

时间复杂度O（sqrt（n））.

map<int, int> prime_factor(int n){
    map<int, int> res;
    for(int i = 2;i * i <= n; i++){
        while(n % i == 0){
            ++res[i];
            n /= i;
        }
    }
    if(n != 1) res[n] = 1;
    return res;
}

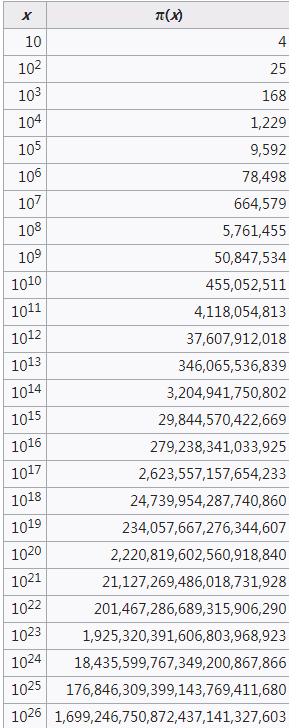
【n以内的素数】

埃氏筛法，时间复杂度O（log（log（n））），近似于O（n）。

//求n以内的素数 
const int n = 10000;   
int prime[n];    //素数数组，prime[i]表示第i个素数 
bool is_prime[n+1];     //is_prime[i]为true表示i是素数

//返回n以内素数的个数 
int sieve(int n){
    int p = 0;
    for(int i = 0;i <= n; i++) is_prime[i] = true;
    is_prime[0] = is_prime[1] = false;
    for(int i = 2;i <= n; i++){
        if(is_prime[i]){
            prime[p++] = i;
            for(int j = 2*i; j <= n; j += i) is_prime[j] = false; 
        }
    }
    return p;
}