51nod 1572 宝岛地图 （预处理四个方向的最大步数优化时间，时间复杂度O（n*m+k））

题目：

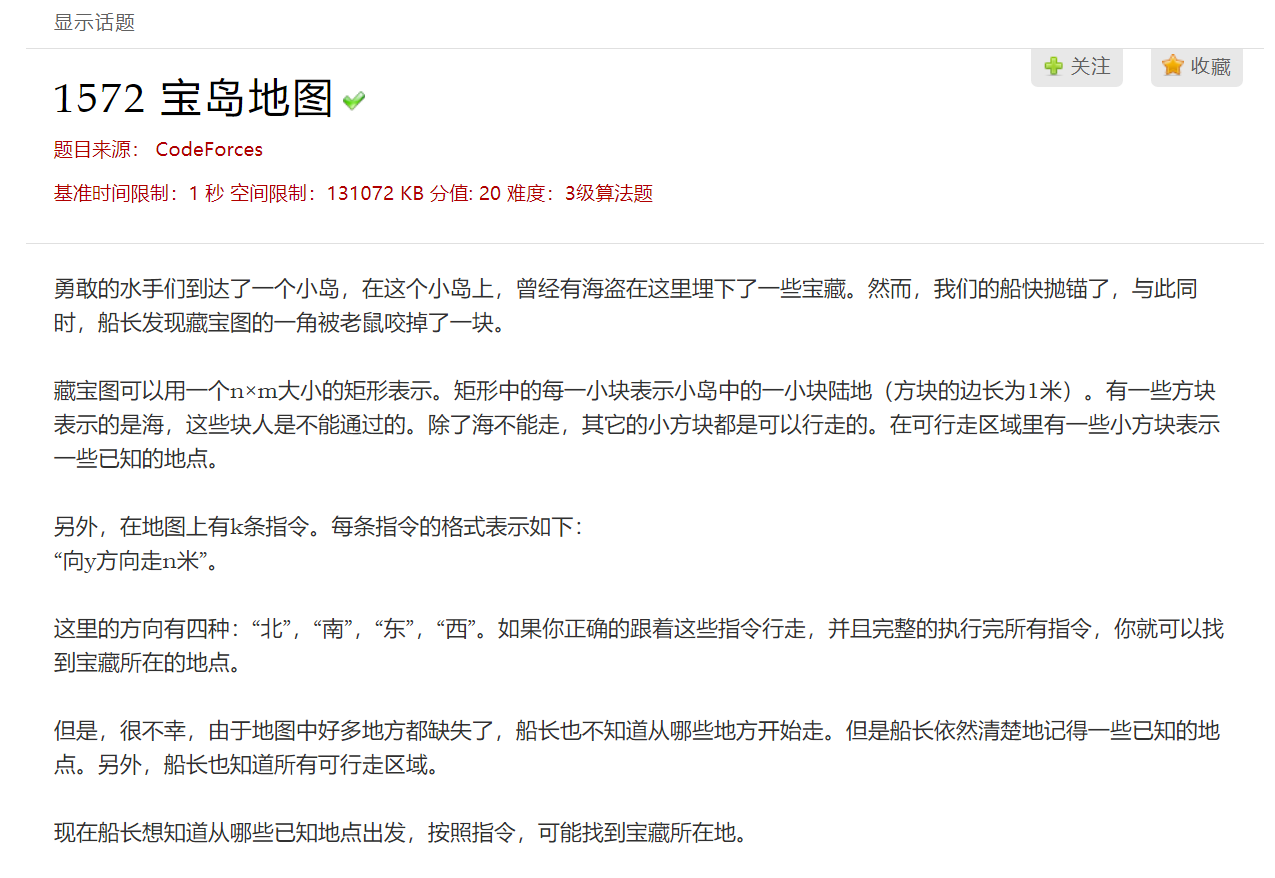
这题如果没有时间限制的话暴力可以解，暴力的话时间复杂度大概是O(k*n)，1s的话非常悬。

所以我们需要换个思路，我们对每个点预处理四个方向最多能走的步数，这个预处理时间复杂度是O(n*m)。

然后对每个字母点模拟一下即可。总时间复杂度O(n*m+k)。不会超时。

提示：没有满足要求的点时，要输出"no solution"，我就在这个上面WA了一次，不然应该可以一次AC的。

代码：

#include <iostream>
#include <algorithm>
#include <stdio.h>
#include <vector>
#include <map>
#include <set>
#include <list>
#include <queue> 
using namespace std;
typedef long long ll;
#define INF 2147483647

// 上N，下S，右E，左W。

//输入 
int n,m,k;
char a[1010][1010];
struct node1{
    int dir;int len;
}t[100010];


//b[i][j][k]表示点(i，j)往方向k最多可以走的步数。 
int b[1010][1010][4]; 

//字母点 
struct node{
    int x;int y;char g;
    bool operator<(node b)
    {
        return g < b.g;
    }
};
list <node> l; 
list <node>::iterator it;


int d[4][2] = {-1,0,1,0,0,1,0,-1};
 
//模拟q这个点走的过程 
bool can(node q) {
    int x = q.x;int y = q.y;
    for(int i = 0;i < k; i++){    
        node1 s = t[i];
        if(b[x][y][s.dir] < s.len) return false;
        x = x + d[s.dir][0]*s.len;
        y = y + d[s.dir][1]*s.len;
    }
    return true;
}
 
int main(){
    //输入数据 
    cin >> n >> m;
    node e;
    for(int i = 1;i <= n; i++) {
        for(int j = 1;j <= m; j++) {
            cin >> a[i][j];
            if(a[i][j] != '#' && a[i][j] != '.'){
                e.x = i; e.y = j; e.g = a[i][j];
                l.push_back(e);
            }
        }
    }
    //对子母点按字典序排序 
    l.sort();
     
    for(int j = 1;j <= m; j++){
        //预处理每个点最多能往北边走多少步 
        int num = 0;
        for(int i = 1;i <= n; i++){
            if(a[i][j] != '#'){
                b[i][j][0] = num;num++;
            }else{
                num = 0;
            }
        }
        //预处理每个点最多能往南边走多少步
        num = 0;
        for(int i = n; i >= 1; i--){
            if(a[i][j] != '#'){
                b[i][j][1] = num; num++;
            }else{
                num = 0;
            }
        }
    }
    
    for(int i = 1; i <= n; i++){
        //预处理每个点最多能往东边走多少步
        int num = 0;
        for(int j = 1;j <= m; j++){
            if(a[i][j] != '#'){
                b[i][j][3] = num; num++;
            }else{
                num = 0;
            }
        }
        //预处理每个点最多能往西边走多少步
        num = 0;
        for(int j = m; j >= 1; j--){
            if(a[i][j] != '#'){
                b[i][j][2] = num; num++;
            }else{
                num = 0;
            }
        }
    }
    
    //把字母方向转换成数字表示 
    cin >> k;
    char key;
    for(int i = 0;i < k; i++){
        cin >> key >> t[i].len;
        if(key == 'N') t[i].dir = 0;
        else if(key == 'S') t[i].dir = 1;
        else if(key == 'E') t[i].dir = 2;
        else if(key == 'W') t[i].dir = 3;
    }
    
    //对每个子母点进行模拟 
    bool flag = false;
    for(it = l.begin();it != l.end(); it++){
        node q = *it;
        if(can(q)){
            cout << q.g;
            flag = true;
        }
    }
    if(!flag) cout << "no solution";
    cout << endl;
    return 0;
}