cdq分治板子题
这篇主要介绍一下cdq分治
顾名思义,cdq分治是一种分治算法(废话)
但是它与普通的分治算法不同:普通的分治算法将问题分解后只需解决子问题,然后回溯统计即可
但是cdq分治需要处理分解后左右区间之间互相的影响
因此变得更加毒瘤
首先简化一下题意:
有 n 个元素,第 i个元素有 ai、bi 、ci三个属性,设三个属性,设f(i)表示满足aj≤ai且bj≤bi且cj≤ci的j的数量
对于 d∈[0,n),求 f(i)=d 的 i的数量。
这个问题貌似不是很好搞的样子...
那么我们简化一下问题:如果是n个“一元组”呢?
那不就是排个序嘛!
排序,然后找出每个数的排名即为答案
如果是二元组呢?
好像没那么简单,但也不难
我们发现,如果x恰好是从1~n的序列,那么这个问题就退化成了经典的逆序对问题!(因为这时x即可看做下标,而y可看做对应的值,那么问题事实上也就是给出一个序列,求他的“非”逆序对数!)
这是否给了我们一些启示呢?
如果x不是顺序的从1~n的排列,怎么样?
那我们就把他排成1~n的排列就好嘛
先按x排序,然后处理y即可
那么,如果x不是一个从1~n的排列呢?
思想没有区别,因为这道题中值的绝对大小作用并不大,因此我们同样可以直接对x排序然后处理y
于是做法是不快要出来了?
回到最开始的问题:
有 n 个元素,第 i个元素有 ai、bi 、ci三个属性,设三个属性,设f(i)表示满足aj≤ai且bj≤bi且cj≤ci的j的数量
对于 d∈[0,n),求 f(i)=d 的 i的数量。
按照最原始的思路,我们首先对x排序,这样就可以只讨论y和z了
然后呢?
如果是二元组,这里可以直接上树状数组求逆序对了
但是由于是三元组,所以无法直接上树状数组
因此本题还有另一种做法:在树状数组每个点上挂一棵平衡树,也就是所谓的“树套树”,然后乱搞(目前本蒟蒻还不会这个方法,只能提供一个思想)
这里不讨论这个方法,还是回到主题:cdq分治法。
(注意:cdq分治主要是一种离线方法,如果要求在线请出门左转找树套树)
我们给出cdq的方法:
首先分解整个区间(分成左右两块),然后对每一块递归处理
在处理完每一块之后,分别将左右两块进行排序(这次按y排,因为x先前排完了),这样就又回到了只有z一维的问题,我们用一个树状数组解之即可
有点抽象,我们举个例子:
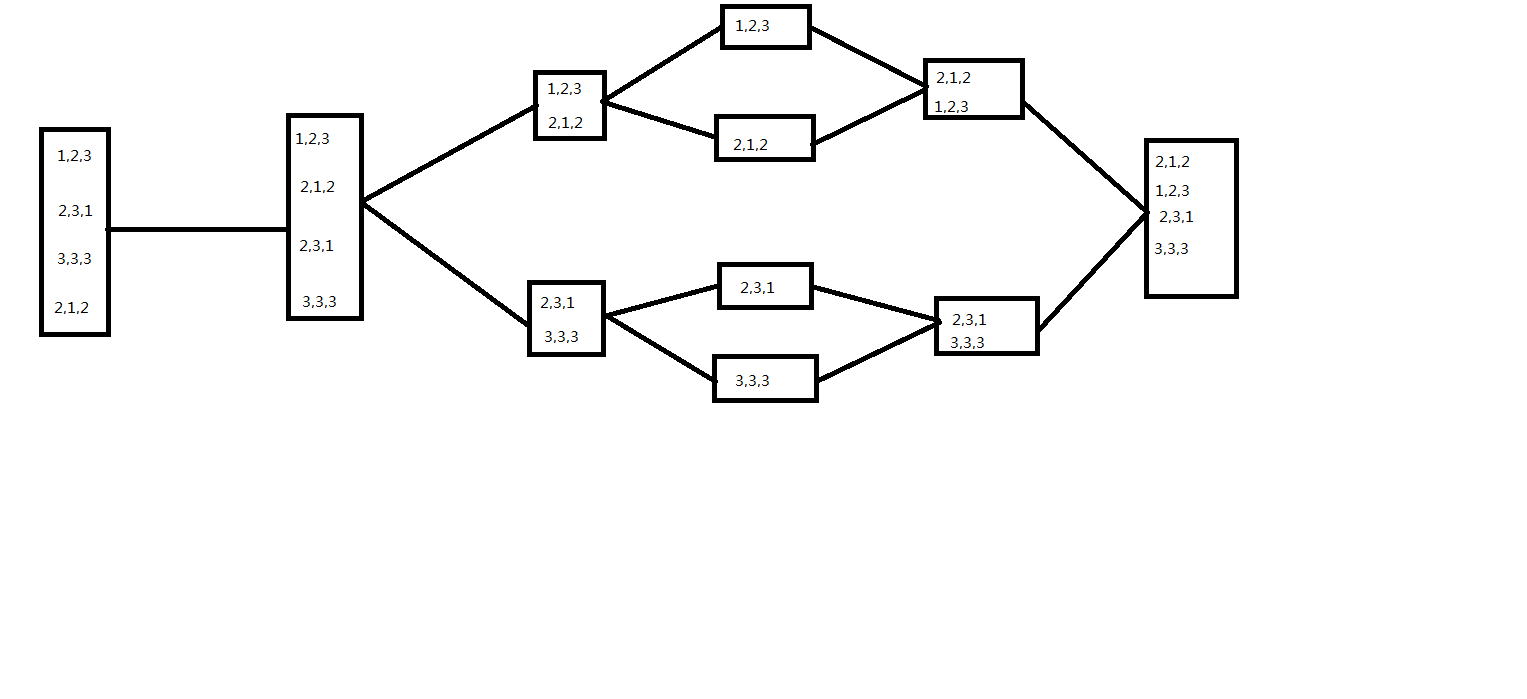
上图给出了一个完整的分治过程,可以看到cdq分治就是这样操作的
我们描述一下合并时的操作:由于事先已经按x排序(如果x相同则按y,否则按z,全一样的需要去重,算成同一个三元组,然后记下这样的三元组的出现次数),所以右区间对左区间不可能产生贡献,我们只需计算左区间对右区间的贡献即可
所以我们对两个区间分别按y排序,用两个指针去扫,如果左指针扫到的y比右指针扫到的y小,就把左指针对应的z扔进树状数组里,直到不能再插入时将右指针对应的z放进树状数组里查询,累计答案即可
然后每次扫完要注意清树状数组(加出现次数相反数即可)
这样我们就完成了统计
可是...等会,答案是什么?
你可能会说:那还不简单,不就是上面累计的东西吗?
不对!
请注意,题目求的是上面累积的东西=d的数量!
所以直接输出上面累计的东西当然不对了!
那么我们怎么统计呢?
这也简单,枚举所有三元组,每个三元组对应的答案即为累计值+重复次数-1(本身不算),然后这个答案的贡献即为该三元组的出现次数
最后输出即可
(有一个小问题,就是事实上,每次不必在合并时排序,仅需在合并完之后排序,这样回溯到上一层之后两个区间就都是有序的了,可以直接操作,而且这样做有个好处,就是由于每次合并时的左右两个区间都是有序的(如果只有一个元素肯定是有序的啊),那么最后排序的话可以用类似归并排序时合并的方法来实现,这个排序复杂度是O(n)的,而如果每次sort的话排序复杂度多个log,所以会慢一些)(但是我懒)
#include <cstdio> #include <cmath> #include <cstring> #include <cstdlib> #include <iostream> #include <algorithm> #include <queue> #include <stack> using namespace std; int n,k; struct node { int x,y,z,d,sum; friend bool operator < (node a,node b) { if(a.x!=b.x)return a.x<b.x; else if(a.y!=b.y)return a.y<b.y; else return a.z<b.z; } }tp[100005],p[100005]; bool cmp(node a,node b) { if(a.y!=b.y)return a.y<b.y; else return a.z<b.z; } int tot=0,dd; int ret[100005]; int s[200005]; int lowbit(int x) { return x&(-x); } void update(int x,int y) { while(x<=k)s[x]+=y,x+=lowbit(x); } int get_sum(int x) { int ans=0; while(x)ans+=s[x],x-=lowbit(x); return ans; } inline int read() { int f=1,x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } void cdq(int l,int r) { if(l==r)return; int mid=(l+r)>>1; cdq(l,mid),cdq(mid+1,r); sort(p+l,p+mid+1,cmp),sort(p+mid+1,p+r+1,cmp); int i=l,j=mid+1; while(j<=r) { while(p[i].y<=p[j].y&&i<=mid)update(p[i].z,p[i].d),i++; p[j].sum+=get_sum(p[j].z),j++; } for(j=l;j<i;j++)update(p[j].z,-p[j].d); } int main() { n=read(),k=read(); for(int i=1;i<=n;i++)tp[i].x=read(),tp[i].y=read(),tp[i].z=read(); sort(tp+1,tp+n+1); for(int i=1;i<=n;i++) { dd++; if(tp[i].x!=tp[i+1].x||tp[i].y!=tp[i+1].y||tp[i].z!=tp[i+1].z)p[++tot]=tp[i],p[tot].d=dd,dd=0;//去重,记录下每个点多少重叠 } cdq(1,tot); for(int i=1;i<=tot;i++)ret[p[i].sum+p[i].d-1]+=p[i].d; for(int i=0;i<n;i++)printf("%d ",ret[i]); return 0; }