题意:
Recently, the nation was shocked by news of Sungai Kim Kim incident in Pasir Gudang, Johor, which has been polluted by chemical waste. Thousands of people who are affected had experienced nausea, dizziness and vomiting, and more than 100 schools were ordered to shut. In order to ensure that such incident will not happen again, an early warning system need o be developed so that residents can make early preparation, and authorities are able to move and act much faster.
A group of scientists has formed a committee to handle the incident, and a smart system with Internet of Things (IoT) sensors was suggested. Numerous sensors which can sense and monitor damages to the environment, either air or water, have been strategically installed around the state, and their coordinates are also recorded. However, the proposed system encountered a failure during its first testing phase. They want you to fix the problem in determining whether the given coordinates of sensors are safe or in the affected areas.
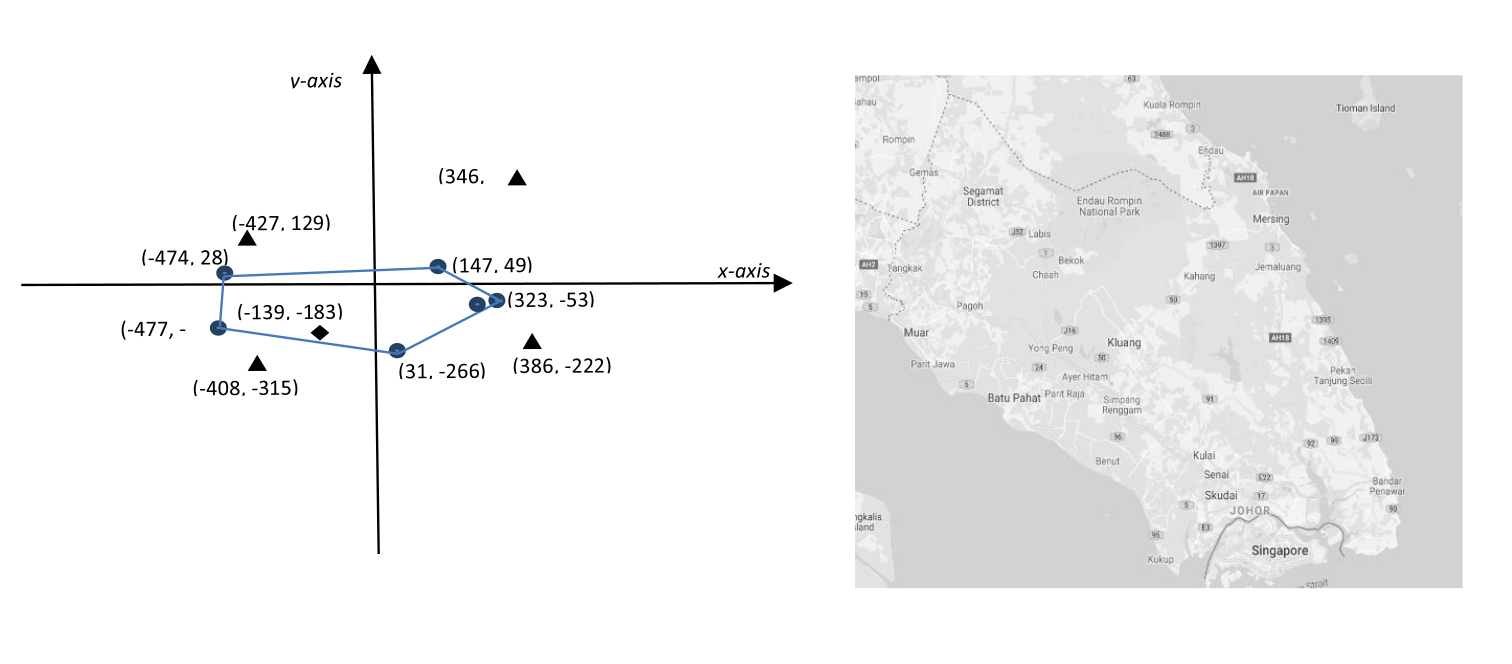
An affected area is defined as the polygon with the minimum length perimeter that can enclose all sensors that trigger warning signal within that area. For example, the sensors (represented by dots) of an affected area and its associated polygon, as well as safe (represented by triangles) and unsafe (represented by diamonds) points of the first dataset are illustrated below.
The input will contain records of data for several test cases of affected areas. The first line of each data set contains a non-negative integer TT, the number of test cases (1≤T≤50).(1≤T≤50). Each test case starts with two non-negative integer CC and PP which is the number of coordinates (3≤C≤50)(3≤C≤50), and points (1≤P≤50)(1≤P≤50), respectively. The next CC lines contain coordinates (x-coordinate, y-coordinate) of each installed sensor, separated with blank spaces. The following PP lines contain coordinates (x-coordinate, y-coordinate) of certain locations in the state, separated with blank spaces. All coordinates are integers between −500−500 and 500500 inclusive.
For each test case, output the following item:
First line: The number of the test cases. The first record corresponds to Case1Case1, the second to Case2Case2 , etc.
Next line: A listing of all the points that appear on the perimeter of the affected area. The points must be identified in the standard form "x-coordinate y- coordinate". The listing must be oriented counter-clockwise and begin and end with the same point.
Last line: For each point of location in the data set, output the line:
x−coordinatey−coordinateisstatusx−coordinatey−coordinateisstatus
where x−coordinatey−coordinatex−coordinatey−coordinate is the coordinate of the location from the input and statusstatus is ′safe′′safe′ or ′unsafe′′unsafe′. A location is considered unsafe it is within the sensor perimeter. A point in exactly at the edge of the perimeter is considered safe.
Each test case must be separated by an empty line. See example.
题解:
#include<bits/stdc++.h> using namespace std; const int maxn=105; const double eps=1e-8; int sgn (double x) { if (fabs(x)<eps) return 0; if (x<0) return -1; else return 1; } struct Point { double x,y; Point () { } Point (double _x,double _y) { x=_x; y=_y; } void input () { scanf("%lf%lf",&x,&y); } double distance (Point p) { return hypot(x-p.x,y-p.y); } Point operator - (const Point &b) const { return Point(x-b.x,y-b.y); } double operator ^ (const Point &b) const { return x*b.y-y*b.x; } bool operator == (const Point &b) const { return sgn(x-b.x)==0&&sgn(y-b.y)==0; } bool operator < (const Point b) const { return sgn(x-b.x)==0?sgn(y-b.y)<0:x<b.x; } }P[maxn]; struct Line { Point s,e; Line () { } Line (Point _s,Point _e) { s=_s; e=_e; } bool pointonseg (Point p) { return sgn((p-s)^(e-s))==0&&sgn((p-s)^(p-e))<=0; } }; struct polygon { int n; Point p[maxn]; Line l[maxn]; void input (int _n) { n=_n; for (int i=0;i<n;i++) p[i].input(); } void getline () { for (int i=0;i<n;i++) l[i]=Line(p[i],p[(i+1)%n]); } struct cmp { Point p; cmp (const Point &p0) { p=p0; } bool operator () (const Point &aa,const Point &bb) { Point a=aa,b=bb; int d=sgn((a-p)^(b-p)); if (d==0) return sgn(a.distance(p)-b.distance(p))<0; return d>0; } }; void norm () { Point mi=p[0]; for (int i=1;i<n;i++) mi=min(mi,p[i]); sort(p,p+n,cmp(mi)); } void Graham (polygon &convex) { norm(); int &top=convex.n; top=0; if (n==1) { top=1; convex.p[0]=p[0]; return; } if (n==2) { top=2; convex.p[0]=p[0]; convex.p[1]=p[1]; if (convex.p[0]==convex.p[1]) top--; return; } convex.p[0]=p[0]; convex.p[1]=p[1]; top=2; for (int i=2;i<n;i++) { while (top>1&&sgn((convex.p[top-1]-convex.p[top-2])^(p[i]-convex.p[top-2]))<=0) top--; convex.p[top++]=p[i]; } if (convex.n==2&&(convex.p[0]==convex.p[1])) convex.n--; } int relationpoint (Point q) { for (int i=0;i<n;i++) { if (p[i]==q) return 3; } getline(); for (int i=0;i<n;i++) { if (l[i].pointonseg(q)) return 2; } int cnt=0; for (int i=0;i<n;i++) { int j=(i+1)%n; int k=sgn((q-p[j])^(p[i]-p[j])); int u=sgn(p[i].y-q.y); int v=sgn(p[j].y-q.y); if (k>0&&u<0&&v>=0) cnt++; if (k<0&&v<0&&u>=0) cnt--; } return cnt!=0; } }; Point a[maxn]; int main () { int T,C,P; scanf("%d",&T); for (int k=1;k<=T;k++) { scanf("%d%d",&C,&P); polygon tt; tt.input(C); polygon tb; tt.Graham(tb); for (int i=0;i<P;i++) { //double x,y; scanf("%lf%lf",&a[i].x,&a[i].y); } //printf(" "); printf("Case %d ",k); int pos; double Minx=1e18,Miny=1e18; for (int i=0;i<tb.n;i++) { if (tb.p[i].x<Minx) { Minx=tb.p[i].x; Miny=tb.p[i].y; pos=i; } else if (tb.p[i].x==Minx&&tb.p[i].y<Miny) { Minx=tb.p[i].x; Miny=tb.p[i].y; pos=i; } } for (int i=pos;i<tb.n;i++) printf("%.0f %.0f ",tb.p[i].x,tb.p[i].y); for (int i=0;i<=pos;i++) printf("%.0f %.0f ",tb.p[i].x,tb.p[i].y); for (int i=0;i<P;i++) { printf("%.0f %.0f is %s! ",a[i].x,a[i].y,tb.relationpoint(Point(a[i].x,a[i].y))==1?"unsafe":"safe"); } printf(" "); } } /* 2 3 2 0 0 0 2 2 0 1 1 2 2 6 2 -1 2 1 2 2 1 2 5 4 4 4 -4 3 2 3 3 */