课时四 多变量线性回归模型
本课时老师讲了多变量线性回归模型,该模型和单变量线性回归模型大致一样,区别就在特征的数量,除了讲解了该模型,还讲了在使用梯度下降算法时可用的几个技巧。下面是课程的主要内容。
1、多维特征
多维特征是指多变量线性回归模型中的多个变量。增添多个特征之后,符号表示就和单变量线性回归有一定的区别:


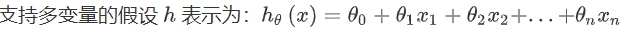

2、多变量梯度下降
多变量线性回归中也有代价函数,也是所有建模误差的平方和,公式如下:
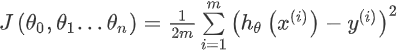
其中:
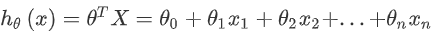
在学了单变量线性回归之后可以明白,多变量线性回归的目标也是找到使得代价函数值最小的一系列参数,利用梯度下降算法也能实现。
首先,梯度下降算法原式是用更新参数值,令参数等于参数减去学习率乘以代价函数的导数,具体如下:

把代价函数带进去并求导化简得到:
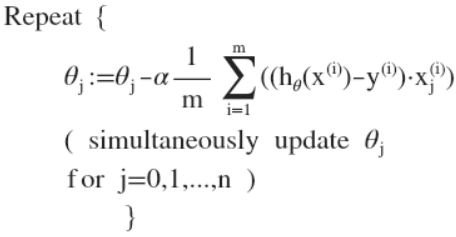
这个化简的过程还比较简单,就是求偏导,和单变量线性回归那个一样。然后就是执行梯度下降算法,迭代执行,直到收敛,确定合适的参数。梯度下降算法的原理在单变量线性回归那节已经弄懂了,这里就不再叙述了。
3、梯度算法使用技巧
3.1、特征缩放
特征缩放是在使用梯度下降算法时会用到的技巧,因为我们在面对多特征问题的时候,不同特征的单位不同,数量级大小也可能不同,我们需要把这些特征调整到相似的尺度,这样有助梯度下降算法更快的收敛。
特征缩放的解决方法是把所有的特征的尺度缩放到-1到1之间,例子如图:
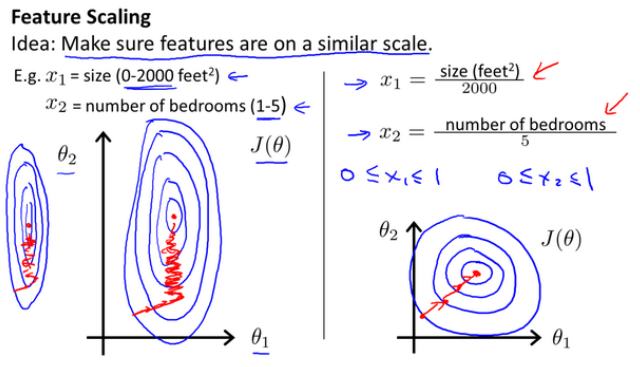
方法一:假设特征x的大小范围是1-200,特征x取值为50,则用x除以x特征值的最大范围200,把这个新值赋给x,通过这样的方法可以把特征值缩放到-1到1之间,如上图所示。
方法二:

3.2、学习率和特征
梯度下降算法的每次迭代受到学习率的影响,如果学习率过小,则达到收敛所需的迭代次数就会很高;如果学习率过大,就可能导致每次迭代不会减小代价函数,越过局部最小值导致无法收敛。
另外一个技巧就是特征选择,例如房价预测问题,给了房屋的长宽两个特征,我们可以不用这俩两个特征,利用长宽求出房屋面积,从而使用面积这一个特征。
线性回归并不适合于所有数据,比如一个二次方模型:
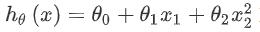
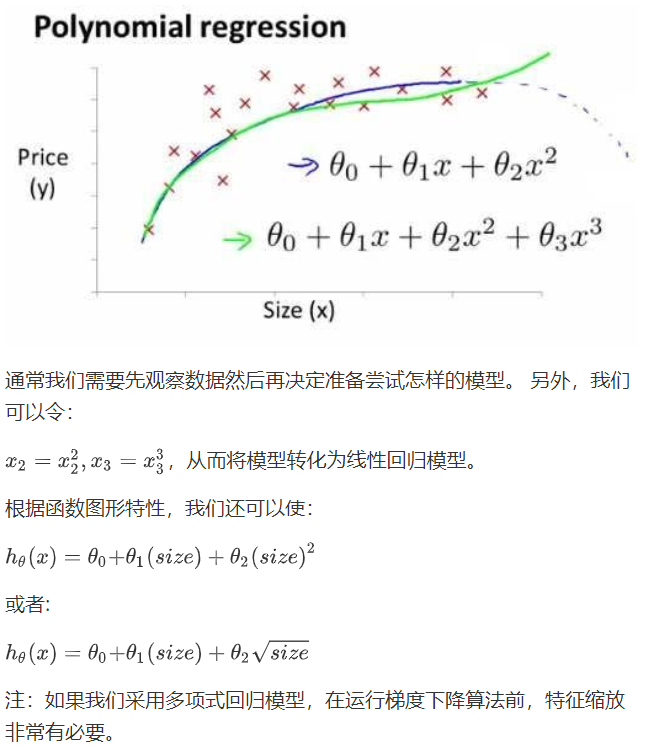
4、正规方程
正规方程是求函数最小值的另外一种方法,有时它会比梯度下降算法更好用,正规方程思想是构造一个关于参数的一元二次方程,然后通过求解下面的方程来找出最合适的参数:
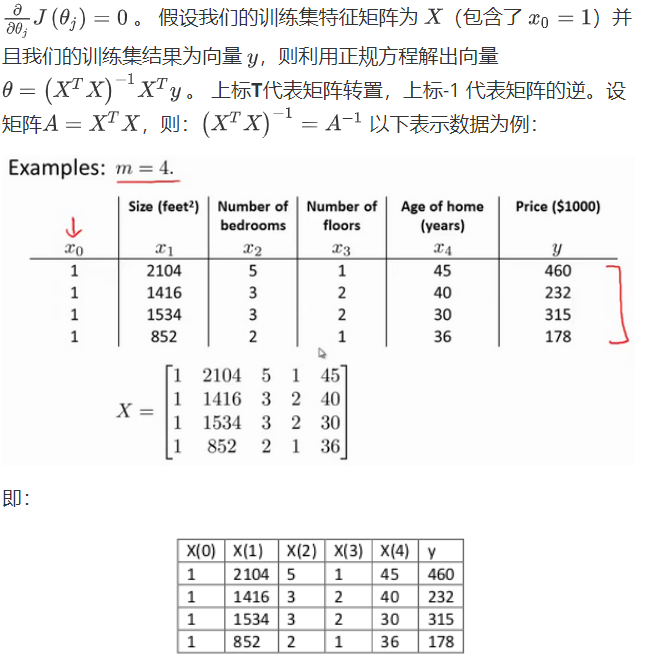
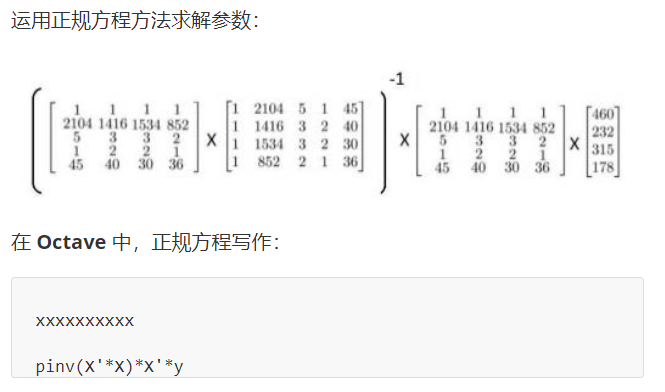
对于不可逆的矩阵,老师有讲,这种情况一般很少出现,即使出现使用pinv命令求逆也是可以的。
利用正规方程求解不需要迭代,只要一步就可以完成,而且只要特征变量的数目不是很大,用正规方程效果都很好。下图是正规方程方法和梯度下降方法的比较:

总结来说,这节课的内容就是多变量线性回归模型,另外又讲了一个新的求最小值的方法,正规方程法。
以上就是课时四的内容,部分笔记来自“机器学习初学者”网站提供的吴恩达老师的2014机器学习课程笔记http://www.ai-start.com/