本文是吴恩达老师深度学习第四周的编程作业,我是参考的文章https://blog.csdn.net/u013733326/article/details/79767169完成的。
首先还是作业要求,此次的作业要求还是和第二周作业要求一样,搭建一个神经网络来识别图片是否是猫。只不过本次作业要求搭建两个网络,一个是两层的,一个是多层的,多层的网络层数可以自定。接下来就是我完成此次作业的流程。
1、准备软件包
import numpy as np import h5py import matplotlib.pyplot as plt import testCases #参见资料包,或者在文章底部copy from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward #参见资料包 import lr_utils #参见资料包,或者在文章底部copy
软件包中有一些是库,有三个是代码文件,这些代码用来加载数据以及激活函数公式和不同激活函数的反向传播公式,这部分的代码我是直接用的博主提供的源码,下载方法可到原博主博客中下载。
软件包准备完之后就可以开始主要程序的编写了,首先我们先把思路捋好,列一下我们要干的活的主要步骤:
-
初始化网络参数
-
前向传播
计算一层的中线性求和的部分
计算激活函数的部分(ReLU使用L-1次,Sigmod使用1次)
结合线性求和与激活函数
-
计算误差
-
反向传播
线性部分的反向传播公式
激活函数部分的反向传播公式
结合线性部分与激活函数的反向传播公式
-
更新参数
这就是我们要做的所有事情,现在我们开始正式搭建两层和多层神经网络。
2、初始化参数
两层的初始化参数的方法,我们在第三周作业中就已经实现了,下面直接放代码:
def initialize_parameters(n_x, n_h, n_y):
"""
此函数是为了初始化两层网络参数而使用的函数。
参数:
n_x - 输入层节点数量
n_h - 隐藏层节点数量
n_y - 输出层节点数量
返回:
parameters - 包含你的参数的python字典:
W1 - 权重矩阵,维度为(n_h,n_x)
b1 - 偏向量,维度为(n_h,1)
W2 - 权重矩阵,维度为(n_y,n_h)
b2 - 偏向量,维度为(n_y,1)
"""
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
# 使用断言确保我的数据格式是正确的
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
初始化多层网络参数的函数:
def initialize_parameters_deep(layers_dims):
"""
此函数是为了初始化多层网络参数而使用的函数。
参数:
layers_dims - 包含我们网络中每个图层的节点数量的列表
返回:
parameters - 包含参数“W1”,“b1”,...,“WL”,“bL”的字典:
W1 - 权重矩阵,维度为(layers_dims [1],layers_dims [1-1])
bl - 偏向量,维度为(layers_dims [1],1)
"""
np.random.seed(3)
parameters = {}
L = len(layers_dims)
for l in range(1, L):
parameters["W" + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) / np.sqrt(layers_dims[l - 1])
parameters["b" + str(l)] = np.zeros((layers_dims[l], 1))
# 确保我要的数据的格式是正确的
assert (parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l - 1]))
assert (parameters["b" + str(l)].shape == (layers_dims[l], 1))
return parameters
这里在写代码时,主要是理解好参数矩阵的维数,这部分的知识老师在课程中讲了,参数w的维数是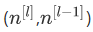 ,b的维数是
,b的维数是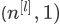 ,只要保证这点就可以了。
,只要保证这点就可以了。
3、前向传播函数
构建完初始化参数函数之后,我们就可以构建前向传播函数了。前向传播分为几部分,首先是计算线性求和部分:Z = np.dot(W,A) + b,然后就是计算激活函数部分:A = relu(Z)或者A = sigmoid(Z)。
线性计算部分:
def linear_forward(A, W, b):
"""
实现前向传播的线性部分。
参数:
A - 来自上一层(或输入数据)的激活,维度为(上一层的节点数量,示例的数量)
W - 权重矩阵,numpy数组,维度为(当前图层的节点数量,前一图层的节点数量)
b - 偏向量,numpy向量,维度为(当前图层节点数量,1)
返回:
Z - 激活功能的输入,也称为预激活参数
cache - 一个包含“A”,“W”和“b”的字典,存储这些变量以有效地计算后向传递
"""
Z = np.dot(W, A) + b
assert (Z.shape == (W.shape[0], A.shape[1]))
cache = (A, W, b)
return Z, cache
这个函数只是计算一个节点的线性部分,下面还会有多层网络中的前向传播方法。
线性激活部分,为了方便调用,我们把这部分功能单组成一个函数。本项目用到两个激活函数,函数的数学形式如下:
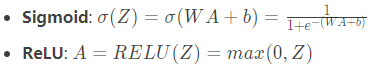
接下来是代码实现:
def linear_activation_forward(A_prev, W, b, activation):
"""
实现LINEAR-> ACTIVATION 这一层的前向传播
参数:
A_prev - 来自上一层(或输入层)的激活,维度为(上一层的节点数量,示例数)
W - 权重矩阵,numpy数组,维度为(当前层的节点数量,前一层的大小)
b - 偏向量,numpy阵列,维度为(当前层的节点数量,1)
activation - 选择在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
返回:
A - 激活函数的输出,也称为激活后的值
cache - 一个包含“linear_cache”和“activation_cache”的字典,我们需要存储它以有效地计算后向传递
"""
if activation == "sigmoid":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
elif activation == "relu":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A, cache
接下来我们利用上面两个函数来实现多层网络中的前向传播函数:
def L_model_forward(X, parameters):
"""
实现[LINEAR-> RELU] *(L-1) - > LINEAR-> SIGMOID计算前向传播,也就是多层网络的前向传播,为后面每一层都执行LINEAR和ACTIVATION
参数:
X - 数据,numpy数组,维度为(输入节点数量,示例数)
parameters - initialize_parameters_deep()的输出
返回:
AL - 最后的激活值
caches - 包含以下内容的缓存列表:
linear_relu_forward()的每个cache(有L-1个,索引为从0到L-2)
linear_sigmoid_forward()的cache(只有一个,索引为L-1)
"""
caches = []
A = X
L = len(parameters) // 2
for l in range(1, L):
A_prev = A
A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], "relu")
caches.append(cache)
AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], "sigmoid")
caches.append(cache)
assert (AL.shape == (1, X.shape[1]))
return AL, caches
在上面的函数中,前L-1层,我们用的激活函数是relu,最后一层的激活函数用的是sigmoid,这个流程也是很好理解。
这样,我们的前向传播函数就完成了,然后我们就开始计算成本。
4、计算成本
成本函数的公式:

def compute_cost(AL, Y):
"""
实施等式(4)定义的成本函数。
参数:
AL - 与标签预测相对应的概率向量,维度为(1,示例数量)
Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量)
返回:
cost - 交叉熵成本
"""
m = Y.shape[1]
cost = -np.sum(np.multiply(np.log(AL), Y) + np.multiply(np.log(1 - AL), 1 - Y)) / m
cost = np.squeeze(cost)
assert (cost.shape == ())
return cost
这样,我们就可以开始反向传播了。
5、反向传播
反向传播主要计算相对参数的损失函数的梯度,流程图如下:
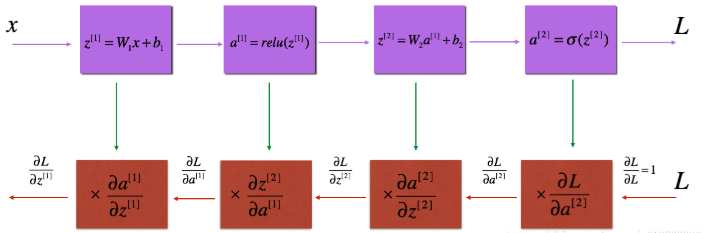
反向传播也包括线性部分和激活部分。首先线性部分:
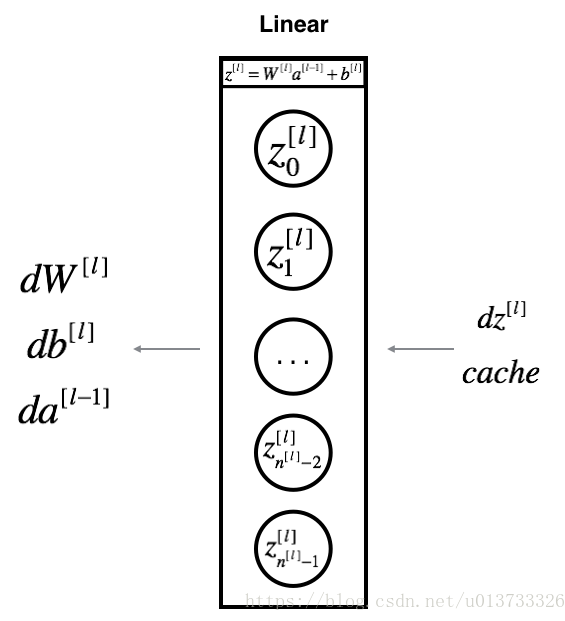


线性部分:
def linear_backward(dZ, cache):
"""
为单层实现反向传播的线性部分(第L层)
参数:
dZ - 相对于(当前第l层的)线性输出的成本梯度
cache - 来自当前层前向传播的值的元组(A_prev,W,b)
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度,与W的维度相同
db - 相对于b(当前层l)的成本梯度,与b维度相同
"""
A_prev, W, b = cache
m = A_prev.shape[1]
dW = np.dot(dZ, A_prev.T) / m
db = np.sum(dZ, axis=1, keepdims=True) / m
dA_prev = np.dot(W.T, dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
线性激活部分:这部分用到了两个函数:sigmoid_backward和relu_backward,这两个函数在博主给的代码中有。
def linear_activation_backward(dA, cache, activation="relu"):
"""
实现LINEAR-> ACTIVATION层的后向传播。
参数:
dA - 当前层l的激活后的梯度值
cache - 我们存储的用于有效计算反向传播的值的元组(值为linear_cache,activation_cache)
activation - 要在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度值,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度值,与W的维度相同
db - 相对于b(当前层l)的成本梯度值,与b的维度相同
"""
linear_cache, activation_cache = cache
if activation == "relu":
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev, dW, db
这只是两层网络的反向传播,然后我们基于此完成多层模型的反向传播。
def L_model_backward(AL, Y, caches):
"""
对[LINEAR-> RELU] *(L-1) - > LINEAR - > SIGMOID组执行反向传播,就是多层网络的向后传播
参数:
AL - 概率向量,正向传播的输出(L_model_forward())
Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量)
caches - 包含以下内容的cache列表:
linear_activation_forward("relu")的cache,不包含输出层
linear_activation_forward("sigmoid")的cache
返回:
grads - 具有梯度值的字典
grads [“dA”+ str(l)] = ...
grads [“dW”+ str(l)] = ...
grads [“db”+ str(l)] = ...
"""
grads = {}
L = len(caches)
m = AL.shape[1]
Y = Y.reshape(AL.shape)
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
current_cache = caches[L - 1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache,
"sigmoid")
for l in reversed(range(L - 1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, "relu")
grads["dA" + str(l + 1)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
6、更新参数
前向传播反向传播都完成之后,我们就可以更新参数了,利用梯度下降法。
def update_parameters(parameters, grads, learning_rate):
"""
使用梯度下降更新参数
参数:
parameters - 包含你的参数的字典
grads - 包含梯度值的字典,是L_model_backward的输出
返回:
parameters - 包含更新参数的字典
参数[“W”+ str(l)] = ...
参数[“b”+ str(l)] = ...
"""
L = len(parameters) // 2 # 整除
for l in range(L):
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
return parameters
至此,我们所需要的所有函数就都完成了,接下来,我们就可以组装这些方法了。
7、搭建两层神经网络和多层神经网络
def two_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False, isPlot=True):
"""
实现一个两层的神经网络,【LINEAR->RELU】 -> 【LINEAR->SIGMOID】
参数:
X - 输入的数据,维度为(n_x,例子数)
Y - 标签,向量,0为非猫,1为猫,维度为(1,数量)
layers_dims - 层数的向量,维度为(n_y,n_h,n_y)
learning_rate - 学习率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每100次打印一次
isPlot - 是否绘制出误差值的图谱
返回:
parameters - 一个包含W1,b1,W2,b2的字典变量
"""
np.random.seed(1)
grads = {}
costs = []
(n_x, n_h, n_y) = layers_dims
"""
初始化参数
"""
parameters = initialize_parameters(n_x, n_h, n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
"""
开始进行迭代
"""
for i in range(0, num_iterations):
# 前向传播
A1, cache1 = linear_activation_forward(X, W1, b1, "relu")
A2, cache2 = linear_activation_forward(A1, W2, b2, "sigmoid")
# 计算成本
cost = compute_cost(A2, Y)
# 后向传播
##初始化后向传播
dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
##向后传播,输入:“dA2,cache2,cache1”。 输出:“dA1,dW2,db2;还有dA0(未使用),dW1,db1”。
dA1, dW2, db2 = linear_activation_backward(dA2, cache2, "sigmoid")
dA0, dW1, db1 = linear_activation_backward(dA1, cache1, "relu")
##向后传播完成后的数据保存到grads
grads["dW1"] = dW1
grads["db1"] = db1
grads["dW2"] = dW2
grads["db2"] = db2
# 更新参数
parameters = update_parameters(parameters, grads, learning_rate)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# 打印成本值,如果print_cost=False则忽略
if i % 100 == 0:
# 记录成本
costs.append(cost)
# 是否打印成本值
if print_cost:
print("第", i, "次迭代,成本值为:", np.squeeze(cost))
# 迭代完成,根据条件绘制图
if isPlot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# 返回parameters
return parameters
def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False, isPlot=True):
"""
实现一个L层神经网络:[LINEAR-> RELU] *(L-1) - > LINEAR-> SIGMOID。
参数:
X - 输入的数据,维度为(n_x,例子数)
Y - 标签,向量,0为非猫,1为猫,维度为(1,数量)
layers_dims - 层数的向量,维度为(n_y,n_h,···,n_h,n_y)
learning_rate - 学习率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每100次打印一次
isPlot - 是否绘制出误差值的图谱
返回:
parameters - 模型学习的参数。 然后他们可以用来预测。
"""
np.random.seed(1)
costs = []
parameters = initialize_parameters_deep(layers_dims)
for i in range(0, num_iterations):
AL, caches = L_model_forward(X, parameters)
cost = compute_cost(AL, Y)
grads = L_model_backward(AL, Y, caches)
parameters = update_parameters(parameters, grads, learning_rate)
# 打印成本值,如果print_cost=False则忽略
if i % 100 == 0:
# 记录成本
costs.append(cost)
# 是否打印成本值
if print_cost:
print("第", i, "次迭代,成本值为:", np.squeeze(cost))
# 迭代完成,根据条件绘制图
if isPlot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
8、预测函数
网络搭建好之后,我们就可以利用他们训练数据集,得到模型之后就可以开始预测了,所以先把预测函数写出来。
def predict(X, y, parameters):
"""
该函数用于预测L层神经网络的结果,当然也包含两层
参数:
X - 测试集
y - 标签
parameters - 训练模型的参数
返回:
p - 给定数据集X的预测
"""
m = X.shape[1]
n = len(parameters) // 2 # 神经网络的层数
p = np.zeros((1, m))
# 根据参数前向传播
probas, caches = L_model_forward(X, parameters)
for i in range(0, probas.shape[1]):
if probas[0, i] > 0.5:
p[0, i] = 1
else:
p[0, i] = 0
print("准确度为: " + str(float(np.sum((p == y)) / m)))
return p
完成之后就可以开始运行项目了,加载数据的方法和第二周编程作业一样,我们先训练两层网络的模型,训练好后,直接进行预测:

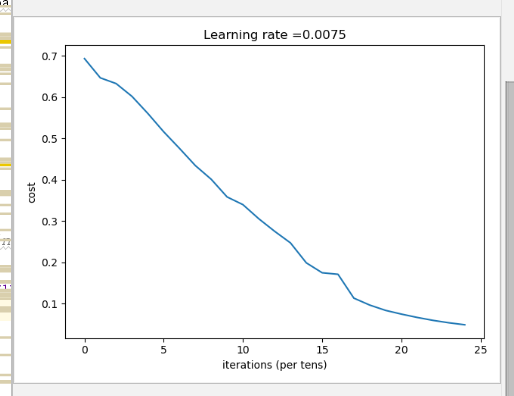
然后我们训练一个多层网络的模型,定义网络层数为5

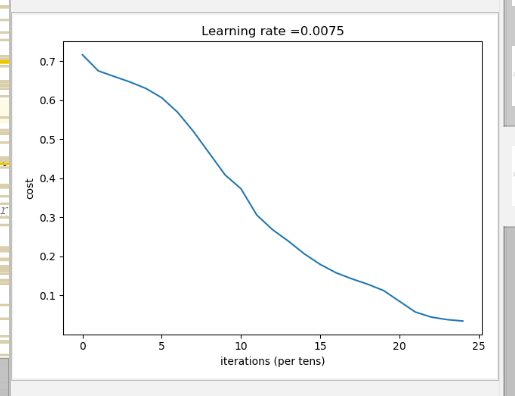
运行代码如下:
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset() train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T train_x = train_x_flatten / 255 train_y = train_set_y test_x = test_x_flatten / 255 test_y = test_set_y layers_dims = [12288, 20, 7, 5, 1] # 5-layer model parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True,isPlot=True) #layers_dims = [12288, 7, 1] # 5-layer model #parameters = two_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True,isPlot=True) pred_train = predict(train_x, train_y, parameters) #训练集 pred_test = predict(test_x, test_y, parameters) #测试集
以上就是此次作业的内容,本次作业难度稍微有所提升,我是完全按照原博主的思路来的,不过还是有些代码不理解,尤其是多层网络那里,还需要慢慢消化,在此也是很感谢原博主细致的文章的讲解。
参考文章:https://blog.csdn.net/u013733326/article/details/79767169