图的定义

图的定义:

1)  一个图(graph)G=(V,E)由顶点(vertex)集V和边(edge)集E组成。

2)  每一条边就是一个点对<v,w>。其中v，w属于V。有时也把边称作弧(arc)。且称v为弧尾(Tail)或初始点(Initial node)。w为弧头(Head)或终端点(Terminal node)。
     如果点对是有序的，那么图就叫做有向的(directed),有向的图叫做有向图(digraph)。
     如果是具有<v,w>和<w,v>,即(v,w)是对称的，是无序对。表示v和w之间的一条边(edge)，此时的图为无向图(Undigraph)。

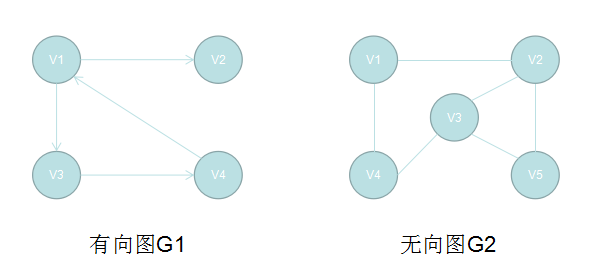
对于G₁的表示为:G₁=(V_1，{A₁})

其中:V1={v1,v2,v3,v4}

        A1={<v1,v2>,<v1,v3>,<v3,v4>,<v4,v1>}    这里的<>括号代表的是有方向的。称之为arc。

对于G₂的表示为:G₂=(V₂，{E₂})

其中:V2={v1,v2,v3,v4,v5}

        E2={(v1,v2),(v1,v4),(v2,v3),(v3,v4),(v2,v5),(v3,v5)}

图的分类:

1. 有1/2n(n-1)条边(edge)的无向图称为完全图(Completed graph)。
2. 有n(n-1)条弧(arc)的有向图称为有向完全图。
3. 有很少条边或弧(e<nlogn)的图为稀疏图(Sparse graph)。
4. 有很多条边或弧(e>nlogn)的图为稠密图(Dense graph)。

其他术语:

1. 在图的边或弧上具有相关的数，此数字称之为权(Weight)。
2. 假设有两个图G=(V,{E})和G'=(V',{E'})，如果V'属于V，E'属于E，称G'为G的子图(Subgraph)。
3. 顶点V的度(Degree)是和v相关联的数目，记为TD(V)。

• • 以顶点V为头的弧的数目为V的入度(InDegree),记为ID(V)。
  • 以顶点V为尾的弧的数目为V的出度(Outdegree),记为OD(V)。

举例:

         在有向图G1中，顶点V1的入度ID(v1)=1,出度OD(v1)=2。度TD(v1)=1+2=3.