幺正矩阵的分解

参考文献：Dita P. Factorization of Unitary Matrices[J]. Journal of Physics A, 2003, 36(11): 2781-2789.

（我主机中的文件：《2003Dita.docx》《2003Dita.pdf》）

n*n 幺正矩阵 U(n) 的独立参数为 n² 个，证明如下：

  

---

  

---

结论：

　　Any unitary matrix  An can be factored into an ordered product of (2n-1) matrices of the form

${A_n} = left[ {{d_n}{O_n}} ight]left[ {d_{n - 1}^1O_{n - 1}^1} ight] cdots left[ {d_2^{n - 2}O_2^{n - 2}} ight]d_1^{n - 1}$

 

---

举个例子，当 n=4 时：

---

　　上面把幺正矩阵参数化的方法其用途为：任意给出 n² 个实数，都可以构造出相应的 n*n 幺正矩阵。

　　我现在考虑的问题是：如何把一个大的幺正矩阵分解为一些小幺正矩阵的直积的和？

　　当 n=4, 对于任意给定的 U（4）可以分解为4项的和：

　　

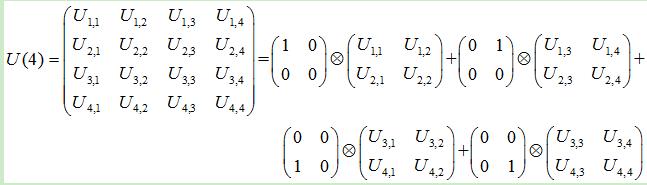
　　当 n=8, U（8）可以分解为16 项的和，如前四项为：

　　

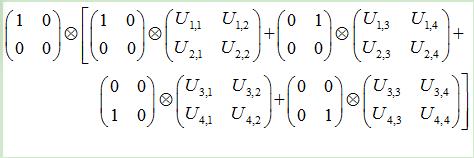
　　观察发现这其实是一个迭代过程,  对于N-qubit, 幺正矩阵为n*n, 分解的项数为 m

　　n=2^N ;  m=4^N-1

---

　　上面2部分结合起来看，对于一些特殊的幺正门，如 CZ，CNOT，swap 门，我们可以直接写出按小矩阵的分解式，也可以确定对应的‘相位参数’ 和 ‘ 转角参数 ’。

　　详情见 cdf 文件：Unitary4_factor.cdf