详解隐马尔科夫模型

隐马尔科夫模型

摘要

本文重点讲解隐马尔科夫(HMM)模型的模型原理，以及与模型相关的三个最重要问题：求解、解码和模型学习。

隐马尔科夫模型的简单介绍

为了方便，下文统一用HMM代替隐马尔科夫模型。HMM实际上是一种图概率模型。之所以叫做隐马尔科夫模型，是因为模型与普通的马尔科夫模型不同的是，HMM含有隐变量空间，并且遵循马尔科夫假设。这样说太抽象，我们看下图：

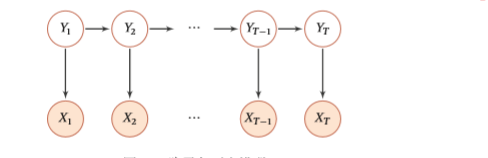
其中(Y_iin Q={q_1,q_2,...,q_N})，(X_i in V={v_1,v_2,...,v_M})。并且记观测序列(X = X_1,X_2,...,X_T)

隐状态序列(Y = Y_1,Y_2,...,Y_T)。我们首先介绍HMM三个重要参数，然后下面再解释这些参数的具体物理含义。

[状态转移矩阵： A = [a_{ij}]N imes N \ a_{ij} =P(Y_t=q_j|Y_{t-1}=q_i),i=1,2,...,N\ 观测概率矩阵: B = [b_{jk}]N imes M \ b_{jk} = P(X_t=v_k|Y_t=q_j), j = 1,2,...,N;k=1,2,...,M\ 初始分布： pi=[pi_1,pi_2,...,pi_N]\ pi_i = P(Y_0=q_i),i = 1,2,...,N ]

也就是说，状态转移概率决定了状态间的单步转移情况，而观测发射矩阵决定了从隐状态到观测状态的转移情况。而初始分布决定了模型的状态初始分布。为了叙述方便，我们记上面的参数为(lambda=(A,B,pi))

HMM有如下两个假设，齐次性质假设和观测独立性假设，分别叙述如下：

• 齐次马尔科夫假设：

[P(Y_t|X_1,...,X_{t-1},Y_1,...,Y_{t-1})=P(Y_t|Y_{t-1}) ]

也就是任何时刻的隐藏状态只与上一时刻的隐藏状态有关，与其他的隐藏状态和观测状态无关。

• 观测独立性假设：

[P(X_t|X_1,...,X_T,Y_1,...,Y_T)=P(X_t|Y_t) ]

即任意时刻的观测只由其同时刻的隐状态所决定，与其他隐藏状态和观测状态无关。

为了更形象的理解这个模型，下面举一个我觉得比较贴切的例子。

假设有两个人分别记为P1和P2，他们中间隔了一堵墙。其中P1被关在了墙里面，P2在外面。这两个人仅仅能通过一个窗子交流。两个人分别有以下的特点：P1记性特别差，只能记住上一次说过的单词。并且每次说话时也只受上一次说话内容所影响。而P2可以看成一个特殊的转录机，他每次说的单词都只受P1当前说的单词所影响。并且P2有一个很长的纸带，会把每次说的单词记录下来。并且假设P1和P2的词汇表都是有限的。

• 如果给定P2的文本片段，我们能否给出该文本片段的概率(已知模型参数(lambda))

• 给定P2的文本片段，假设我们已经知道了P1的词汇表，我们能否给出P1最可能说了哪段话（已知模型参数(lambda))

• 给定大量的(P2,P1)文本对片段，能否推测出模型参数(lambda),或者仅仅给出大量的P2文本片段，能否学出模型参数(lambda)

实际上面的三个问题就对应着预测，解码和模型学习的三个问题。并且如果P1的词汇表是分词标记标签，P2的词汇表是汉语，那么所对应的就是分词问题。把P1的词汇表是命名实体标签，P2的词汇表是汉语，那么所对应的问题实际上就是命名实体识别（NER）问题。

如果我们不关心模型的具体使用，只是关心HMM是一个什么样的模型，那么到这里完全可以将模型说明白。但是我们要更细致的了解HMM的话（从代码层面上）那么还是逐一解决上述三个重要的问题。

预测问题

所谓的预测问题，实际上是求下面的序列概率：

[p = P(X_1,X_2,...,X_T;lambda) ]

根据全概率公式我们有：

[egin{align*} p&=P(X_1,X_2,...,X_T;lambda)\ &=sum_{Y}P(X_1,X_2,...,X_t,Y_1,Y_2,...,Y_t;lambda) end{align*} ]

其中(Y)是隐状态空间的内所有组合，显然当隐状态空间特别大时，如果通过简单的枚举加和方式，面临着指数爆炸这一难题（简单的分析可知，上述的求和复杂度是(O(N^T))）。

通过上述分析可知，高效的求解序列概率的关键在于求解联合概率。根据链式法则及HMM的假设我们可以得到如下公式：

[egin{align*} P(X_{<=T},Y_{<=T};lambda)& = P(X_1,X_2,...,X_T,Y_1,Y_2,...,Y_T;lambda) \ &=P(X_T,Y_T|X_1,...,X_{T-1},Y_1,...,Y_{T-1}) cdot P(X_1,...,X_{T-1},Y_1,...,Y_{T-1})\ &=P(X_T|Y_T) cdot P(Y_T|Y_{T-1})cdot P(X_{<T},Y_{<T}) end{align*} ]

其中前两步分别是观测独立假设和齐次转移假设，最后一步是我们的递归定义。实际上上面的公式还能进一步拆分（根据递归定义拆解下去即可），这里不再展开说明。

根据链式法则，我们可以有以下结论，(T)时刻的概率计算仅仅依赖于(T-1)时刻，又涉及到指数状态空间枚举，那么实际上一定会存在着大量的重复计算，这样我们就会想用动态规划来进行优化。（这样的思考确实有些跳跃，实际上我在刚刚接触HMM时，也对于其中反复运用的动态规划感到跳跃，但是等我刷过一些算法题目之后，再回头看HMM，其中运用的动态规划便顺理成章了。

首先我们定义(alpha_{t,j}) 为(t)时刻对应的(Y_{t}=q_j且观测序列为X={X_1,...,X_t})的全（路径）概率。那么显然根据上面的定义，我们有：

[P(X_{<=T};lambda) = sum_{j=1}^Nalpha _{T,j} ]

并且，特别的，对于(t=1)时，我们引入上面的初始分布：

[alpha_{1,j} = pi_jcdot b_{j,X_1} ]

总结上面的算法，伪代码叙述如下：

输入：观测序列X,模型参数 lambda = (A,B,pi)
输出：序列X所对应的概率p

[egin{align*} &初始化： alpha_{1,j} = pi_jcdot b_{j,X_1}\ &动态递推：alpha_{t,j} = sum_{i=1}^Nalpha_{t-1,i}cdot a_{i,j}cdot b_{j,X_t}\ &结束求和： p = sum_{j=1}^N alpha_{T,j} end{align*} ]

对应的python代码(片段）如下：

def forward_alpha(self,label_seq):
    T = len(label_seq)
    label_seq_idx = self.label_to_idx(label_seq)
    init_label_idx = label_seq_idx
    pre_alpha = [self.pi[j] * self.b[j][init_label_idx] for j in range(self.N)]
    for t in range(1,T):
        tmp_label_idx = label_seq_idx[t]
        tmp_alpha = [self.sum_vector([pre_alpha[i]*self.a[i][j] * b[j][tmp_label_idx]])
                     for j in range(self.N)]
        pre_alpha = tmp_alpha
     return self.sum_vecotr(tmp_alpha)

解码问题

解码问题是指给出观测序列，我们给出与之相对应的概率最大的隐序列，形式化表述如下：

[Y^* = argmax_{Y}P(Y|X;lambda) ]

为了方便，我们将条件概率(P(Y|X;lambda))记为(p)，由于HMM并没有直接建模条件概率，因此我们需要将其展开，下面推导如何求解(Y^*),对于同一个序列(X),(P(X;lambda))都相同，所以有以下公式成立：

[egin{align*}Y^*&=argmax_YP(Y|X;lambda)\&=argmaxfrac{P(Y,X;lambda)}{P(X;lambda)}\&=argmaxP(Y,X;lambda)end{align*} ]

最后一步和上面的前向计算公式何其的相似啊，不考虑效率的话，我们同样可以通过枚举隐状态空间的所有的可能，然后计算一个最大值，但是这样又面临着指数爆炸的问题。因此我们需要著名的viterbi解码算法，实际上viterbi解码算法就是动态规划，但是由于针对这样的解码问题太著名了，所以专门有了这种著名的称呼。既然viterbi是动态规划算法，那么必然少不了定义转移状态，定义(delta_t(j))为下面的概率：

[delta_t(j)=P(X_{<=t},Y_{<t}^*,Y_t=q_j) ]

根据以上定义，显然有以下关系成立：

[egin{align*}p^*&=P(Y^*,X)\&=maxP(Y,X)\&=maxP(X_{<=T},Y^*_{<T},Y_t=q_j),j=1,...,N\&=maxdelta_T(j),j=1,...,Nend{align*} ]

之所以上述公式成立，我们可以这样思考，假设从开始时刻1到结束时刻(T)的最优路径为

[Y*={q_1^*,...,q_t^*,...,q_T^*} ]

那么，显然显然从(t)时刻到(T)时刻的所有以(q_t^*)开始，以(q_T^*)结尾的所有路径中，上述路径一定是最优的那一条，入若不然，那么我们将其替换为另外那条最优的，则得到了另外一条全局最优的路径，这显然和上面的定义矛盾。所以当我们已知从开始时刻1到(t)时刻的最优路径之后，便可以得到下一步的最优路径了。递推转移公式如下：

[delta_t(j)=maxdelta_{t-1}(i)cdot a_{i,j}cdot b_{j_,X_t},i=1,2,...,N ]

如果这对这步骤的递推理解上有些跳跃的话，请将上述(delta_t(j))的定义写出来，然后结合HMM的两个基本假设，便十分清楚了。

重新整理上面的求解最大概率的步骤如下：

[egin{align*}初始化&:delta_1(j)=pi_jcdot b_{j,X_1}\递归求值&:delta_t(j)=max(delta_{t-1}(i)cdot a_{i,j}cdot b_{j,X_t}),t=2,...,T;{i,j}=1,...,N\返回最优值&:p^*=maxdelta_T(j),j=1,..,Nend{align*} ]

上述便是利用viterbi来求解最优路径所对应概率的过程，但是别忘了，我们是为了求出最优概率所对应的那条路径，所以我们还需要通过回溯的方法去求得最优路径，思想就是通过像深度优先搜索那样，每次记录当前状态的上一状态的最优值，这样，从最后时刻以此回溯，便能够找出所有的最优路径。同样的，这也是一个动态规划的过程，我们记(phi_t(j))为(t)时刻隐藏状态所对应的(t-1)时刻最优路径所对应的状态值，那么显然有以下递推关系成立：

[egin{align*}初始化&: phi_1(j) = 0,j=1,2,...,N\递推&:phi_t(j) = argmaxdelta_{t-1}(i)cdot a_{i,j},t=2,3,...,T;{i,j}=1,...,N\回溯求解初始化&:Y_T^*=argmaxdelta_T(j),j=1,2,...,N\回溯求解&:Y_{t-1}^*=phi_t(Y_t^*),t=T,T-1,...,2\返回解码结果&:Y^*=reversed(Y_T^*,Y_{T-1}^*,...,Y_1^*)end{align*} ]

对照上面的公式，请认真思考两个关键的问题:

• 为什么(phi_t(j))要这样定义
• 上面的递推和求解最优概率的递推有什么不同，在什么地方有差异。

同样的，我们给出viterbi的python代码如下：

    def viterbi(self,label_seqs):
        label_seqs_idxs = [self.label_to_idx.get(label,label_to_idx['unk']) 
                           	    for label in label_seqs]
        T = len(label_seqs)
        last_alpha,tmp_alpha = [],[]
        start = label_seqs_idxs[0]
        last_alpha = [self.pi[i] * self.B[i][start] for i in range(self.N)]
        parent_state = [[] for j in range(T)]
        for t in range(1,T):
            label = label_seqs_idxs[t]
            tmp_alpha = [max([last_alpha[j] * self.A[j][i] * self.B[i][label] 
 							for j in range(self.N)])
                         		for i in range(self.N)]
            parent_state[t] = [self.argmax([last_alpha[j] * self.A[j][i] 
                            for j in range(self.N)])
                         		for i in range(self.N)]
            last_alpha = tmp_alpha
        ans = []
        parent = self.argmax(tmp_alpha)
        ans.append(parent)
        for t in range(T-1,0,-1):
            parent = parent_state[t][parent]
            ans.append(parent)
        return max(tmp_alpha),list(reversed(ans))

同样的，完整的代码戳这里，代码写的应该还所清晰，所求解的例子也是统计学习方法的例题，建议动手写一下代码，以便深刻理解这个过程。

实验

实验后续补上，计划在人民日报语料上做命名实体识别，并和神经网络进行比较。

参考文献：

《统计学习方法》第二版，李航，隐马尔科夫模型

《神经网络与深度学习》，邱锡鹏，概率图模型