机器学习(六) 梯度下降法 (下)

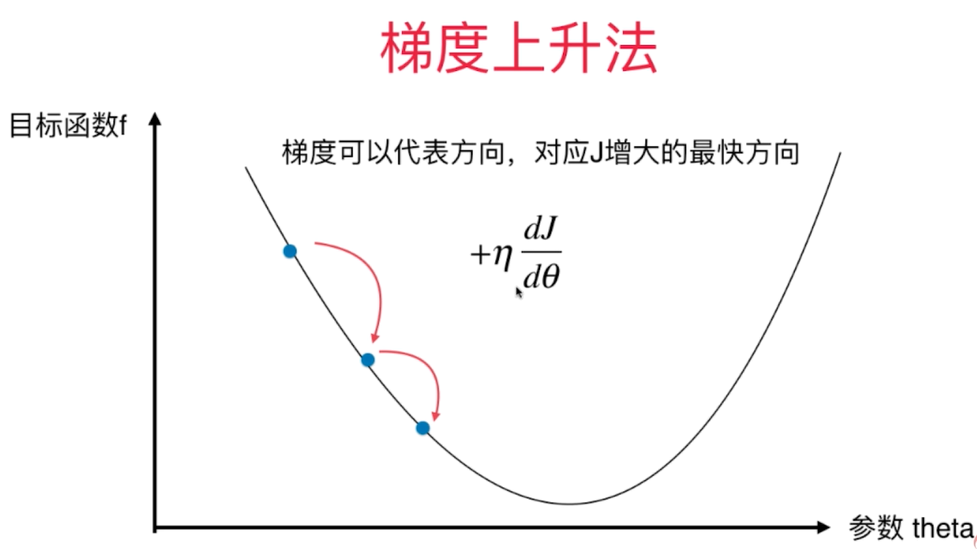
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景：一个人被困在山上，需要从山上下来(i.e. 找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走，同理，如果我们的目标是上山，也就是爬到山顶，那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷

作者：六尺帐篷
链接：https://www.jianshu.com/p/c7e642877b0e
來源：简书
简书著作权归作者所有，任何形式的转载都请联系作者获得授权并注明出处。

五、梯度下降法中的向量化和数据标准化

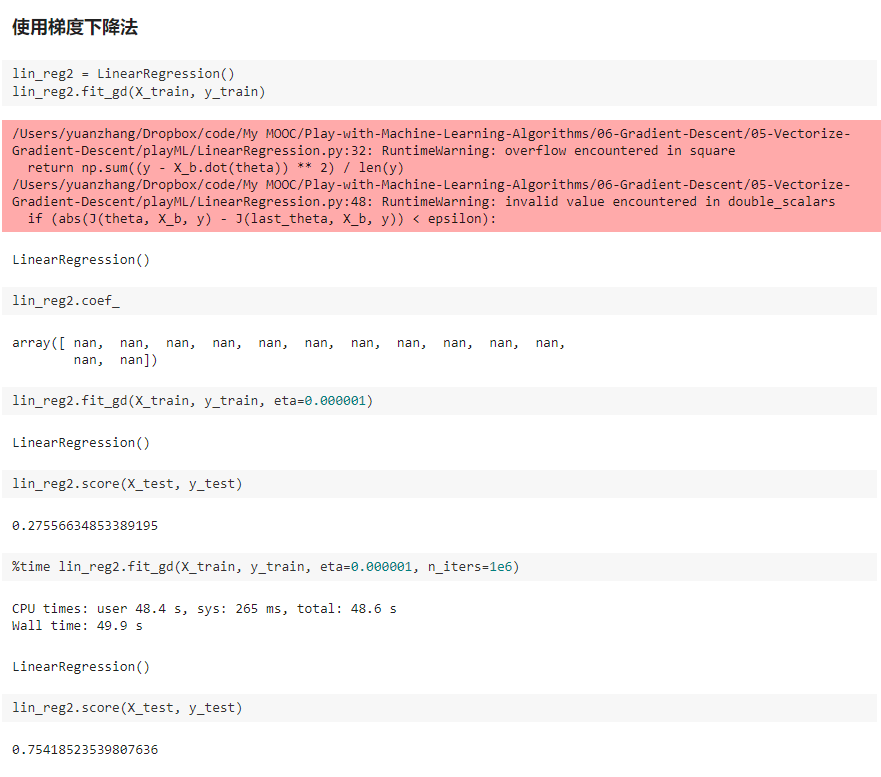
六、随机梯度下降法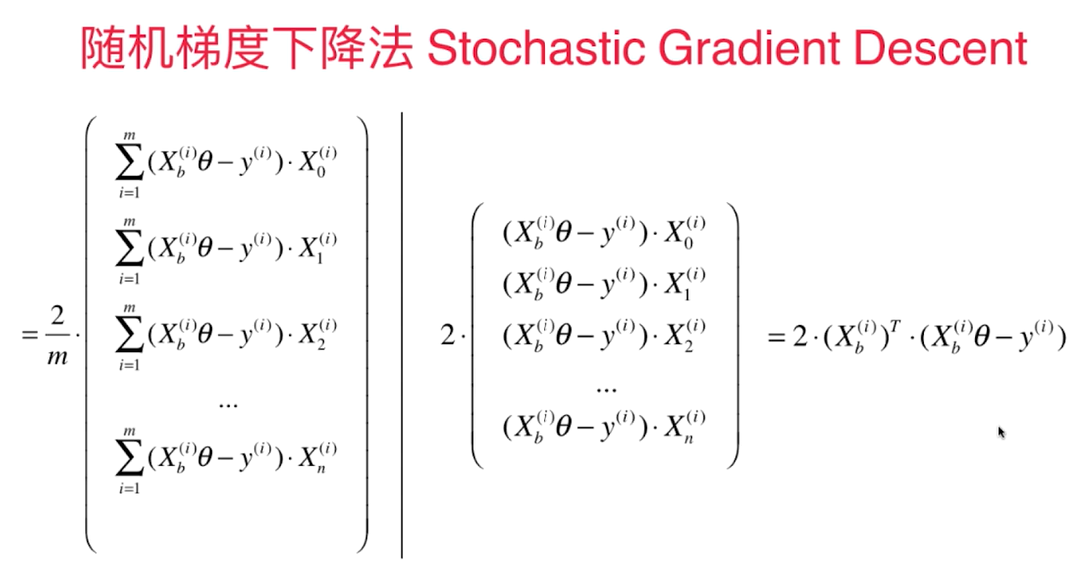

 

 

 

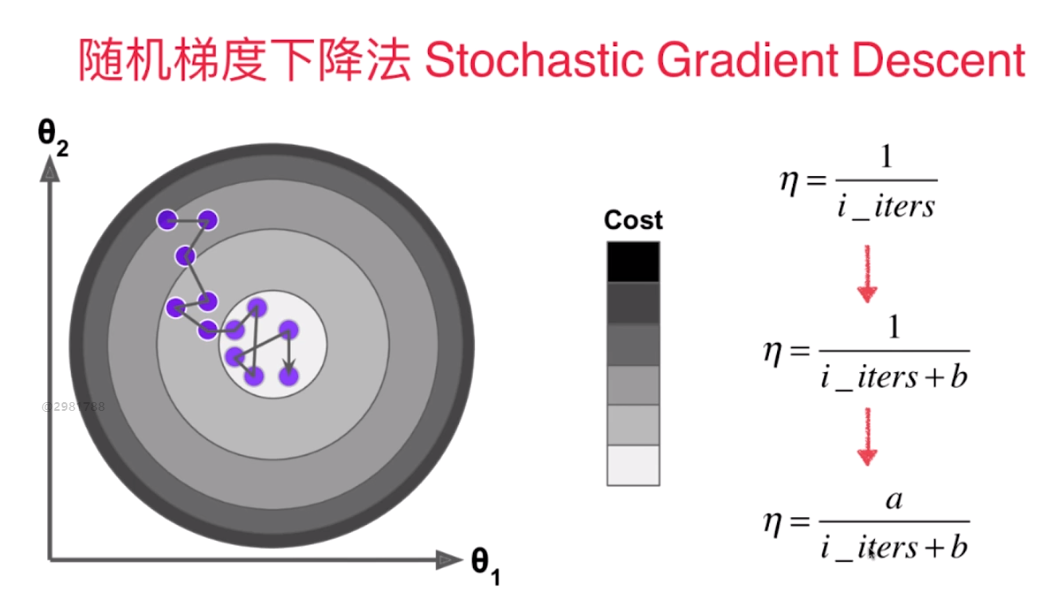
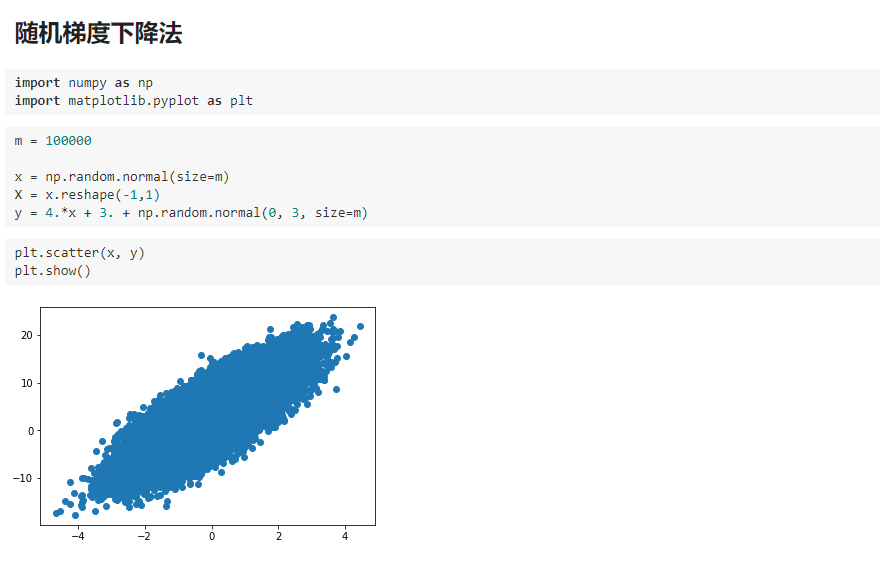
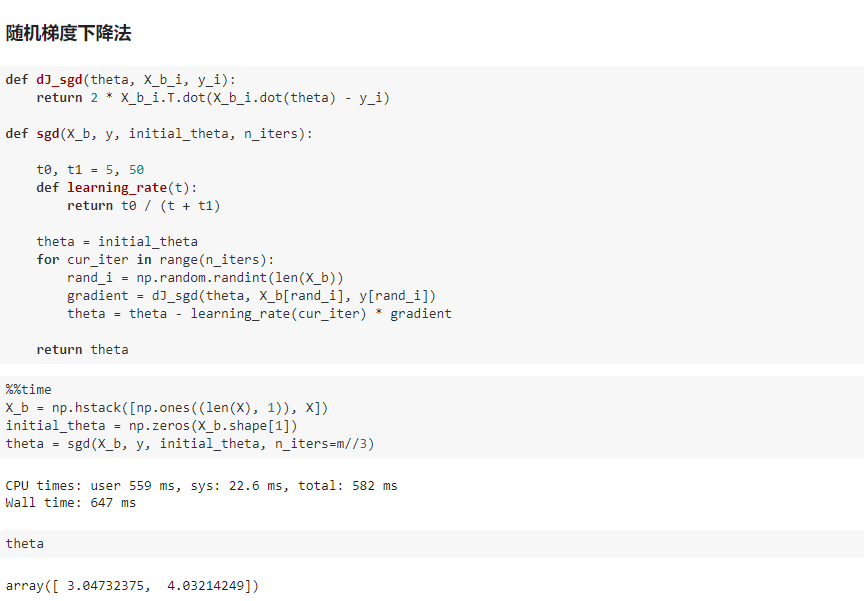
七、scikit-learn中的随机梯度下降法

LinearRegression.py

import numpy as np
from .metrics import r2_score

class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], 
            "the size of X_train must be equal to the size of y_train"

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def fit_bgd(self, X_train, y_train, eta=0.01, n_iters=1e4):
        """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], 
            "the size of X_train must be equal to the size of y_train"

        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
            except:
                return float('inf')

        def dJ(theta, X_b, y):
            return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)

        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

            theta = initial_theta
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break

                cur_iter += 1

            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def fit_sgd(self, X_train, y_train, n_iters=50, t0=5, t1=50):
        """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], 
            "the size of X_train must be equal to the size of y_train"
        assert n_iters >= 1

        def dJ_sgd(theta, X_b_i, y_i):
            return X_b_i * (X_b_i.dot(theta) - y_i) * 2.

        def sgd(X_b, y, initial_theta, n_iters=5, t0=5, t1=50):

            def learning_rate(t):
                return t0 / (t + t1)

            theta = initial_theta
            m = len(X_b)
            for i_iter in range(n_iters):
                indexes = np.random.permutation(m)
                X_b_new = X_b[indexes,:]
                y_new = y[indexes]
                for i in range(m):
                    gradient = dJ_sgd(theta, X_b_new[i], y_new[i])
                    theta = theta - learning_rate(i_iter * m + i) * gradient

            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.random.randn(X_b.shape[1])
        self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, 
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), 
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

 

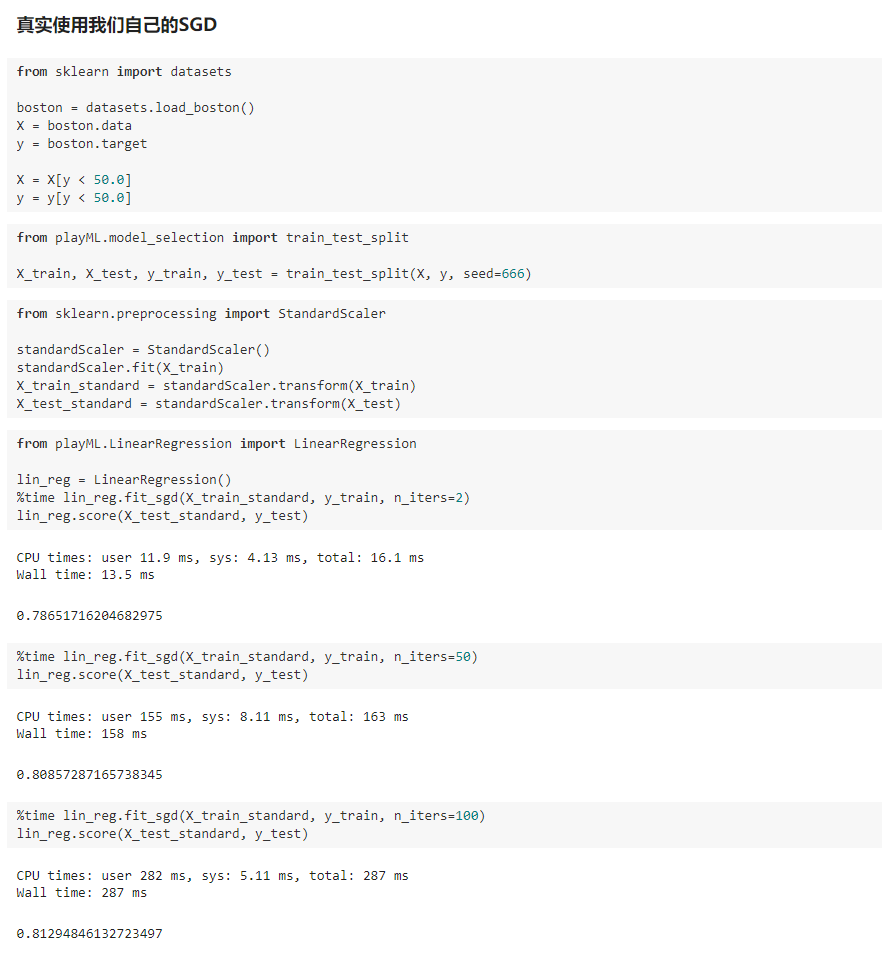
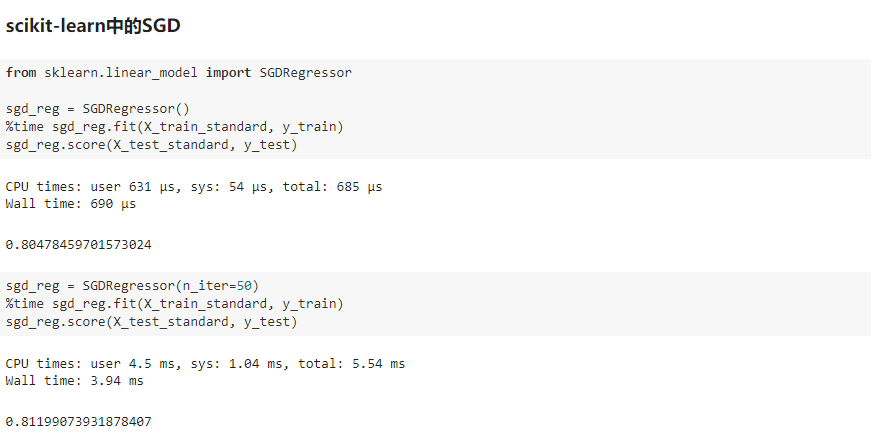
八、如何确定梯度计算的准确性？调试梯度下降法

 

 

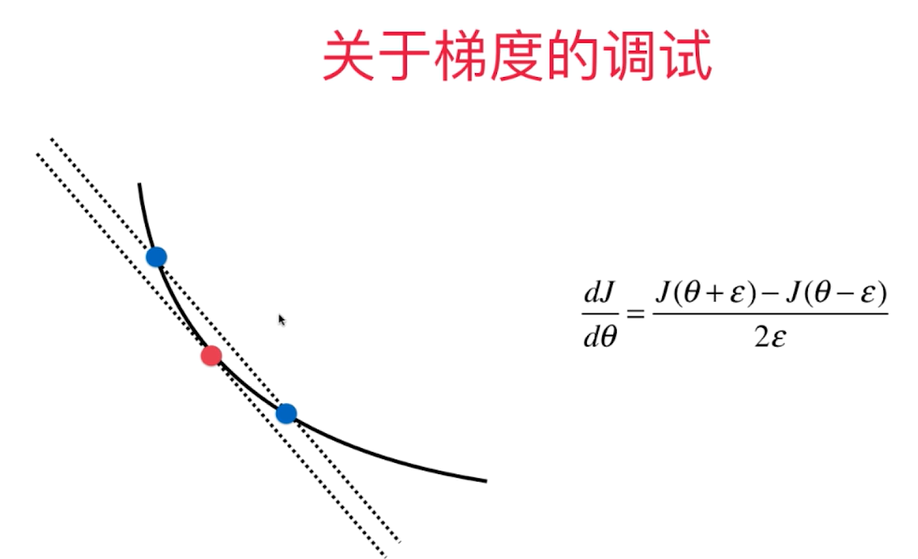
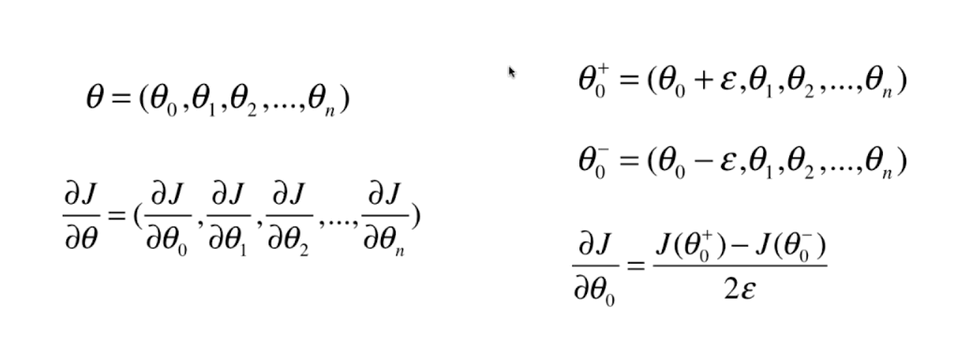
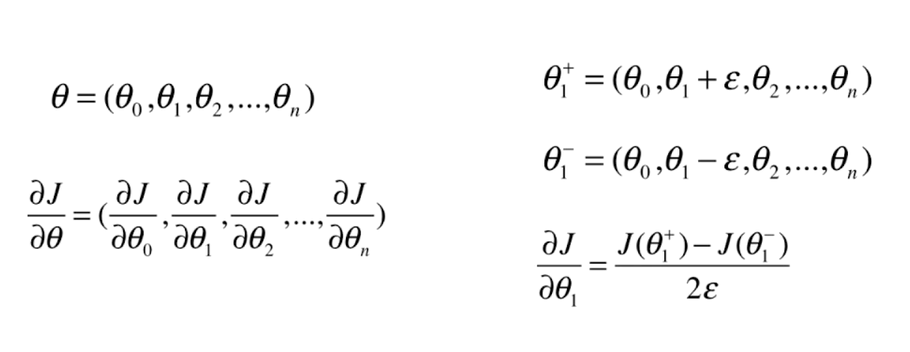
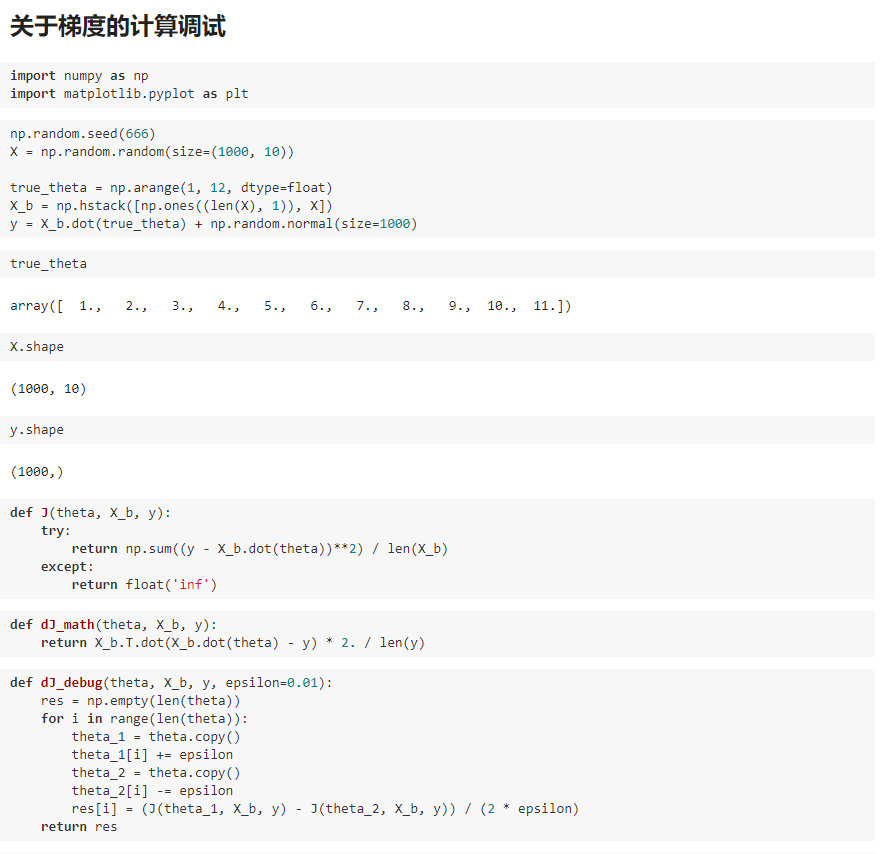
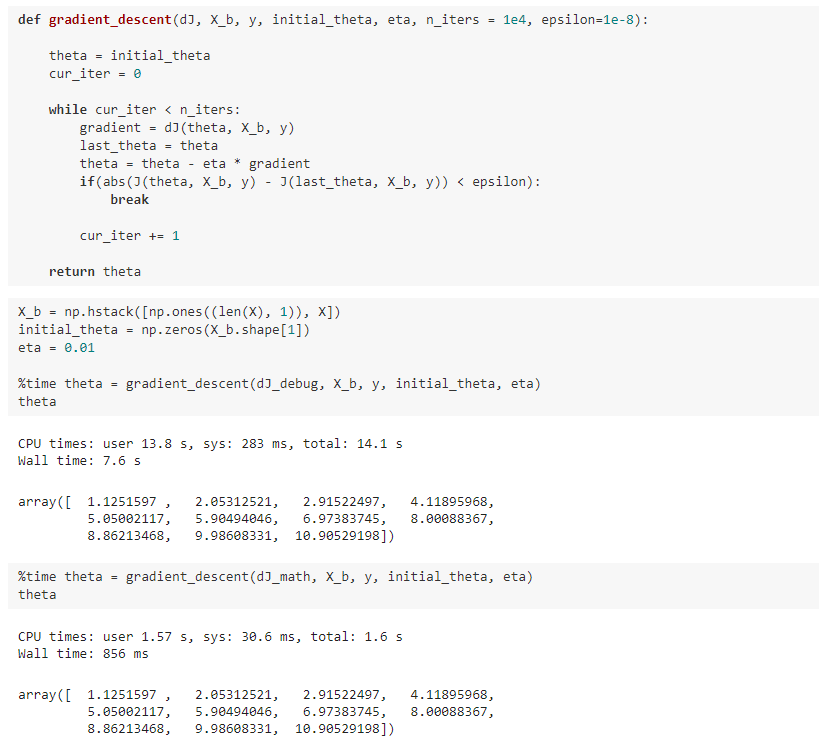
九、有关梯度下降法的更多深入讨论

  我写的文章只是我自己对bobo老师讲课内容的理解和整理，也只是我自己的弊见。bobo老师的课 是慕课网出品的。欢迎大家一起学习。