当插值的要求涉及到对插值函数导数的要求时,普通插值问题就变为埃尔米特插值问题。拉格朗日插值和牛顿插值的要求较低,只需要插值函数的函数值在插值点与被插函数的值相等,以此来使得在其它非插值节点插值函数的值能接近被插函数。但是有时候要求会更高,不仅要插值函数与被插函数在插值节点函数值相等,而且要求它们的导数相等。
其实此时的情况并没有变得复杂,解决这个问题的思路与拉格朗日插值法的思路是相同的,不同点在于插值条件的约束函数增加了导数一项,原来由于0~n插值节点有n+1个插值节点,需要求出n+1个线性方程的解,(因为实打实的去求这样一个线性方程组的难度颇高)也就是需要构造一个不超过n+1-1 = n次的多项式,这里减1是因为n次多项式会解出n+1个解,还有一个常数。
当每一个插值节点再有一个对于导数的约束条件时,此时线性方程变成了2*(n + 1)= 2n + 2个,也就是需要构造一个不超过2n+1次的多项式。
构造出的埃尔米特插值函数应该是这样一个形式:
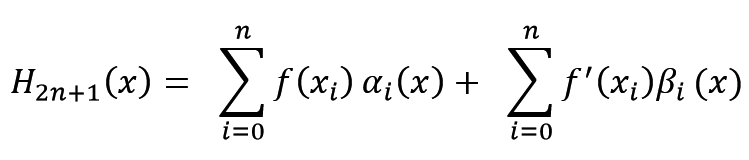
可以看出就是再拉格朗日插值函数的基础上添加对导数的约束。
构造埃尔米特插值的关键时构造基函数![]() 与
与![]() 。
。
如何构造这两个基函数我并不了解,但是可以想办法网上凑,只需要他们满足以下约束即可:
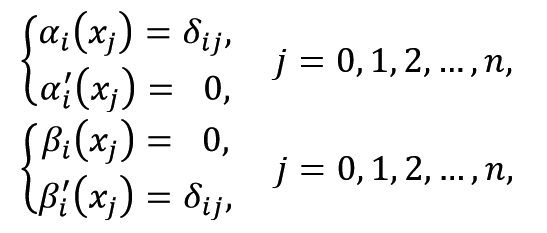
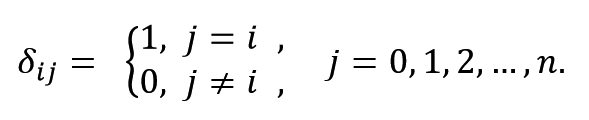
我在这里贴一个满足要求的![]() 与
与![]() 。
。
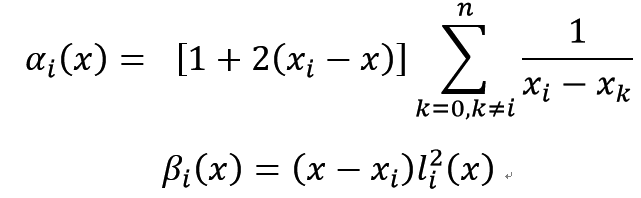
其中![]() 为拉格朗日插值基函数的平方。
为拉格朗日插值基函数的平方。
将以上两个基函数带入埃尔米特插值多项式便得到了插值函数。
开始贴代码:
首先贴的是拉格朗日插值基函数:
"""
@brief: 获得拉格朗日插值基函数
@param: xi xi为第i个插值节点的横坐标
@param: x_set 整个插值节点集合
@return: 返回值为参数xi对应的插值基函数
"""
def get_li(xi, x_set = []):
def li(Lx):
W = 1; c = 1
for each_x in x_set:
if each_x == xi:
continue
W = W * (Lx - each_x)
for each_x in x_set:
if each_x == xi:
continue
c = c * (xi - each_x)
# 这里一定要转成float类型,否则极易出现严重错误. 原因就不说了(截断误差)
return W / float(c)
return li
接着根据插值节点获得埃尔米特插值多项式需要的两个基函数:
"""
@brief: 获得埃尔米特插值基函数α(x) notice: 非求导部分基函数
@param: xi xi为第i个插值节点的横坐标
@param: x_set 整个插值节点集合
@return: 返回值为参数xi对应的插值基函数
"""
def get_basis_func_alpha(xi, x_set = []):
def basis_func_alpha(x):
tmp_sum = 0
for each_x in x_set:
if each_x == xi:
continue
tmp_sum = tmp_sum + 1/float(xi - each_x)
return (1 + 2*(xi-x) * tmp_sum) * ((get_li(xi, x_set))(x)) ** 2
return basis_func_alpha
"""
@brief: 获得埃尔米特插值基函数β(x) notice: 求导部分基函数
@param: xi xi为第i个插值节点的横坐标
@param: x_set 整个插值节点集合
@return: 返回值为参数xi对应的插值基函数
"""
def get_basis_func_beta(xi, x_set = []):
return lambda x : (x - xi) * ((get_li(xi, x_set))(x)) ** 2
最后便可以构造埃尔米特插值函数了:
"""
@brief: 获得埃尔米特插值函数
@param: x 插值节点的横坐标集合
@param: fx 插值节点的纵坐标集合
@param: deriv 插值节点的导数集合
@return: 参数所指定的插值节点集合对应的插值函数
notice:
经过对拉格朗日插值法, 牛顿插值法, 埃尔米特插值法的测试发现, 内插效果很好,
外插基本无法使用,误差极大(不能叫误差, 应该叫错误).
"""
def get_Hermite_interpolation(x = [], fx = [], deriv = []):
set_of_func_alpha = [] # α(x)基函数集合
set_of_func_beta = [] # β(x)基函数集合
for each in x: # 获得每个插值点的基函数
tmp_func = get_basis_func_alpha(each, x)
set_of_func_alpha.append(tmp_func) # 将集合x中的每个元素对应的插值基函数保存
tmp_func = get_basis_func_beta(each, x)
set_of_func_beta.append(tmp_func) # 将集合x中的每个元素对应的插值基函数保存
def Hermite_interpolation(Hx):
result = 0
for index in range(len(x)):
result = result + fx[index]*set_of_func_alpha[index](Hx) + deriv[index]*set_of_func_beta[index](Hx) #根据根据拉格朗日插值法计算Lx的值
return result
return Hermite_interpolation
下面看一下效果:

对以上几个插值节点进行插值后获得了如下效果:
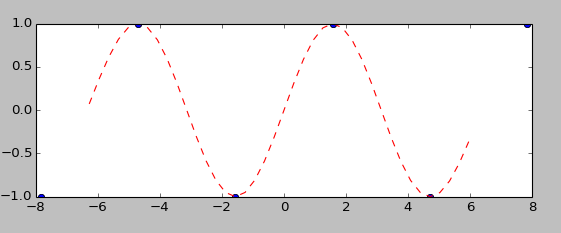
效果非常棒。
以上图像的测试代码如下:
"""
demo:
"""
if __name__ == '__main__':
''' 插值节点, 这里用二次函数生成插值节点,每两个节点x轴距离位10 '''
import math
sr_x = [(i * math.pi) + (math.pi / 2) for i in range(-3, 3)]
sr_fx = [math.sin(i) for i in sr_x]
deriv = [0 for i in sr_x] # 导数都为 0
Hx = get_Hermite_interpolation(sr_x, sr_fx, deriv) # 获得插值函数
tmp_x = [i * 0.1 * math.pi for i in range(-20, 20)] # 测试用例
tmp_y = [Hx(i) for i in tmp_x] # 根据插值函数获得测试用例的纵坐标
''' 画图 '''
import matplotlib.pyplot as plt
plt.figure("play")
ax1 = plt.subplot(211)
plt.sca(ax1)
plt.plot(sr_x, sr_fx, linestyle = ' ', marker='o', color='b')
plt.plot(tmp_x, tmp_y, linestyle = '--', color='r')
plt.show()
通过观察以上的原理观察,实际上在以后遇到更高要求的插值问题时,比如要求插值函数与被插函数三次,四次导数相等,我们也是可以利用类似的方法,只是构造相应的基函数可能需要一番功夫,计算复杂度也会上升。