分段二次插值——用Python进行数值计算

　　事实上在实际使用中，高次插值显然是很不适合的，高次插值将所有样点包涵进一个插值函数中，这是次幂高的原因。高次计算复杂，而且刚开始的一点误差会被方的很大。因此将整个区间分为若干个小区间，在每一个小区间进行插值这样更好，实现容易，也方便在一些嵌入式设备上使用。有不少需要插值方法的场景是在嵌入式的应用中。

　　我以等距节点的二次插值为例，以每三个节点为一个子区间。

　　等距节点二次插值很好写，由于每个区间只有三个插值节点，计算差商也不必使用拉格朗日插值中使用的递归，直接列表达式也很简单（实际上等距节点二次插值就是只有三个节点的拉格朗日插值，只是此时在定义域内，有很多个拉格朗日插值函数，每个子区间对应一个）。递归的副作用相当的明显，尽管写成尾递归可以减小副作用，但是能避免递归还是避免吧。

　　分段插值函数可以表示为：

　　

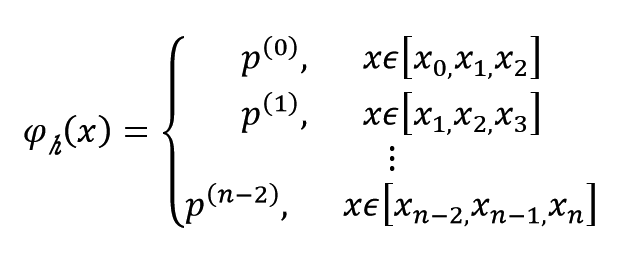
　　每一个插值函数表达式：

　　

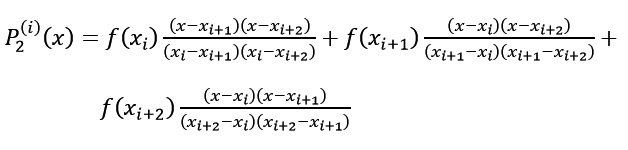
　　如上，不需要用递归求差商，方便很多。一个函数即可搞定。

　　

"""
@brief: 获得分段二次插值函数
@param: x       插值节点的横坐标集合
@param: fx      插值节点的纵坐标集合  
@return: 参数所指定的插值节点集合对应的插值函数
"""    
def get_sub_two_interpolation_func(x = [], fx = []):
      
    def sub_two_interpolation_func(Lx):
        result = 0
        for index in range(len(x)-2):
            if Lx >= x[index] and Lx <= x[index+2]:
                result = fx[index]*(Lx-x[index+1])*(Lx-x[index+2])/(x[index]-x[index+1])/(x[index]-x[index+2]) + 
                         fx[index+1]*(Lx-x[index])*(Lx-x[index+2])/(x[index+1]-x[index])/(x[index+1]-x[index+2]) + 
                         fx[index+2]*(Lx-x[index])*(Lx-x[index+1])/(x[index+2]-x[index])/(x[index+2]-x[index+1])
        return result
            
    return sub_two_interpolation_func
    

　　

     
"""
demo:
"""
if __name__ == '__main__':   

    ''' 插值节点, 这里用二次函数生成插值节点，每两个节点x轴距离位10 '''
    sr_x = [i for i in range(-50, 51, 10)]
    sr_fx = [i**2 for i in sr_x]
    
    Lx = get_sub_two_interpolation_func(sr_x, sr_fx)            # 获得插值函数
    tmp_x = [i for i in range(-45, 45)]     # 测试用例
    tmp_y = [Lx(i) for i in tmp_x]          # 根据插值函数获得测试用例的纵坐标
        
    ''' 画图 '''
    import matplotlib.pyplot as plt
    plt.figure("play")
    ax1 = plt.subplot(111)
    plt.sca(ax1)
    plt.plot(sr_x, sr_fx, linestyle = ' ', marker='o', color='b')
    plt.plot(tmp_x, tmp_y, linestyle = '--', color='r')
    plt.show()

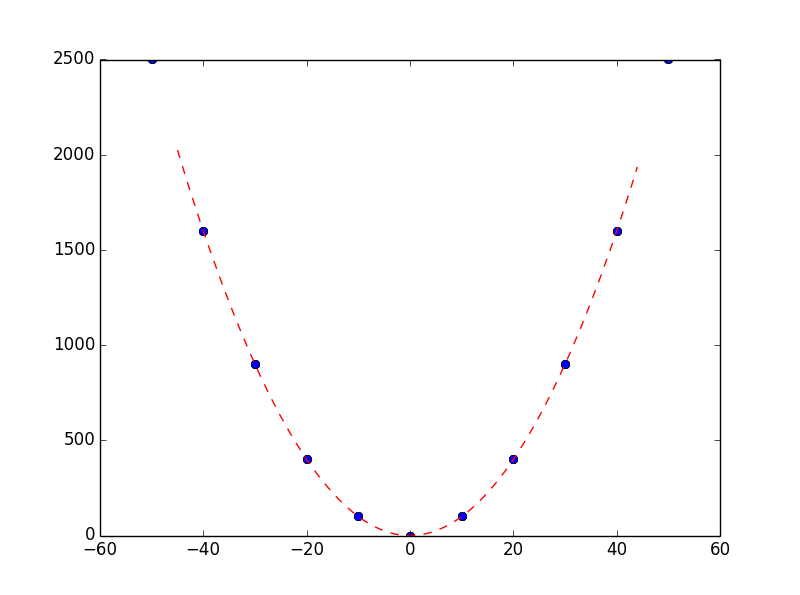
　　　　插值函数图像：