差分隐私是为了在敏感数据上进行数据分析而发展起来的一套机制,通过混淆数据库查询结果,来实现数据在个人层面的隐私性,并且保证查询结果近似正确。这篇文章通过一些例子简要介绍差分隐私的提出动机和思想,主要参考Dwork的The Algorithmic Foundations of Differential Privacy[1]和CUHK的CSCI 5520[2]。
1.差分隐私的直观理解(intuitively)
假如我们现在有一个学生表,有三个字段:姓名、性别、考试通过情况。

其中呢,姓名和性别是可以公开的,考试通过情况是个人隐私。我们开放这个数据的查询,但是不想暴露个人的隐私信息——考试通过情况。
现在呢有人想访问一些关于这个数据的信息,要查询Orhan的成绩是什么。这个查询会直接返回隐私信息,我们当然会拒绝这种形式的查询。
用户查询“多少个学生通过了这个考试”,我们认为这种查询涉及到的是总体的信息,没有涉及到个人的隐私信息,可以响应这个查询。
但是查询“有多少个女生没通过这个考试”,乍一看好像没有泄露敏感信息,但是在上面这个数据例子中,是会泄露的,因为只有两个女生(这个信息是公开的),查询响应会是2,能够推导出Aisha和Erica没有通过。
再来看一个常见的例子,医院开放了它们的医疗数据给研究者用于做各种统计分析,为了保护患者隐私,通常会移除数据中的姓名、身份证号等再发布。但是,就算移除了身份信息,利用一些在外部得到的附加数据,也可能会泄露个人的敏感信息,比如通过把开放的医疗数据表与其他渠道得到的带有某人属性(生日、性别等)的数据表进行比对,就能够在原表中锁定对应的个人,从而得到敏感信息。
所以我们需要一种机制,能够对用户查询提供有用的响应,又能够保护数据中的个人隐私。然而现实是,又提供完全精确的查询响应,又能够完全保护隐私,这种条件成立的场景很少见。但是,我们可以通过随机化或近似查询的响应,放松一点精确性,但是数据有较好的隐私性。
结合上面第一个例子,我们可以设计一种随机机制,当张三对数据发起请求查询q,我们不返回给他一个真实的响应A,而是返回A+N,这里N是一个随机变量,它有如下PMF(概率质量函数:离散随机变量在各特定取值上的概率):
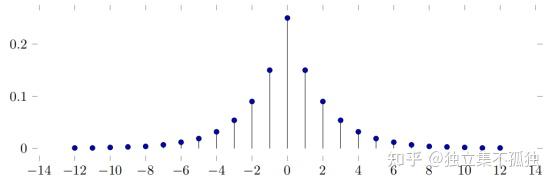
如果查询q的真实响应是A,返回给张三的结果也是A的概率是25%,返回范围在[A-1, A+1]内的概率是55%(25%+30%),返回范围在[A-2, A+2]内的概率是73%,以此类推。
当张三发起请求“有多少个女生没通过这个考试”,我们通过以上机制返回响应1,那张三就比较难断定真实的响应是0,1还是2。假如张三在发起查询前,通过查询整体的通过率,可以认为每个人未通过考试的概率是40%,这个是张三现在对这个数据的认识。那返回给他有1个女生没有通过考试的结果后,张三的认识会有什么变化呢,比如,张三可以认为Aisha未通过考试的概率是多少呢?(答案是张三对数据的认识基本没什么变化,分析如下)
让AF和EF分别表示Aisha和Erica未通过考试,我们想要计算
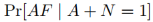
由贝叶斯公式
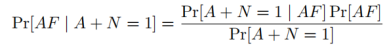
其中,
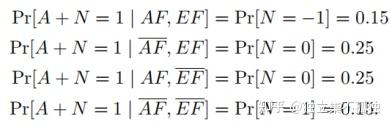
通过平均AF和BF的各种情况,得到
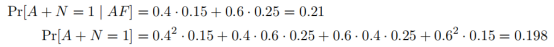
最终得到
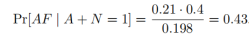
我们可以从以上的计算中看到,张三知道“有多少个女生没通过这个考试”的近似查询结果后,认为Aisha未通过考试的概率从原来的40%变化为了43%。我们可以认为在查询前后,张三对数据中个人隐私的“认知”或者“知识”几乎没有发生变化,对精确的查询结果加上随机变量噪声的近似方式,加强了数据的隐私性。
2.隐私的定义
下面我们用数学语言来描述“在查询前后对单个人的隐私认知几乎不发生变化”(semantic privacy),即语义隐私,然后给出一种差分隐私的定义(differential privacy),最后证明这两种隐私定义的关系。
我们先约定一些符号:
是一个集合,数据库的每一行在这个集合里取值,比如
是所有的三元组(姓名,性别,考试通过情况)组成的集合,我们固定数据库的行数为
,那么一个数据库
是幂集
(
的所有子集组成的集合)中的一个元素。查询是一个函数
,输入数据库
,输出某些值。
为附加到查询q的随机机制,输入一个数据库
,得到一个随机化的查询结果(对应上个例子的A+N这个操作)
为数据库随机变量,
表示数据库第
行内容
为定义在数据库行上的映射,比如输出考试通过情况
表示概率分布
定义1 一个定义域为 的机制
,如果对于每个
,每个数据库
,每种
,每种可能的
的输出
,都满足
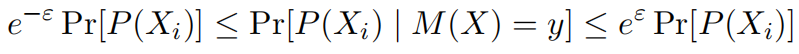
则说机制M满足ε-语义隐私。
我们来看一个极端的设定,当 ,得到
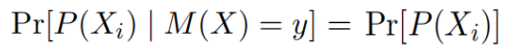
也就是说在得到 的查询响应y前后,
在第
行上的概率是完全相同的,也可以说在第
行上的先验概率和后验概率是相同的,观察
的响应后不会揭露第
行任何的附加信息。满足这种情况的机制
有极好的隐私性,但是也不会提供关于这个数据库的任何信息了。所以,一般让ε 取一个比较小的数,比如0.05,让
满足这种条件就可以了,前后的概率仍然相似,又能通过
获得一些有用的信息。
下面我们定义差分隐私,差分隐私比语义隐私在使用上更方便,并且差分隐私蕴含语义隐私。
定义2 如果对于每一对只有一行不相同的数据库 和
,以及每种可能的
的输出
,都满足
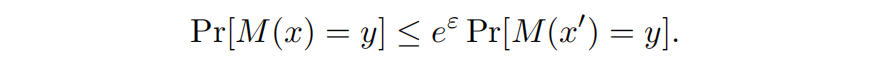
则说机制M满足ε-差分隐私。
我们再来看当 的情况,得到
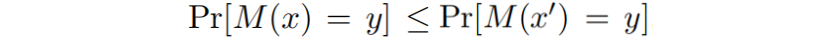
然后调换 和
的角色,我们可以得到另一个方向的不等式,结合通过这两个不等式只有得到
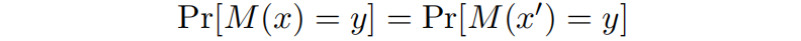
因为这个等式对所有的 都成立,只有
和输入没半毛钱关系才行,也就是说独立于输入,那这个查询自然不会反映这一对输入的数据库的信息。也是一般让ε 取一个比较小的数,得到一些折中。
通过调换 和
的角色,我们也能得到

直白地说,就是只有一行不同的两个数据库,进行查询机制 后,这两个数据库分别得到的结果有相似的概率分布。
那语义隐私与差分隐私有什么关系呢?可以证明,如果 是满足ε-差分隐私的,则
是满足ε-语义隐私。证明过程可参考[2]
而且使用差分隐私的定义比语义隐私要更方便,要验证一个机制是满足差分隐私,我们只需要证明对于每一对只有一行不同的数据库,这个机制的不能充分区分它们,而不是像语义隐私,要考虑每个数据库、每一行、每种 的先验和后验概率。
3.拉普拉斯机制
拉普拉斯机制是一种满足差分隐私的机制,主要是应用在计数查询(查询返回的是非负整数组成的向量,为了讨论方便,只考虑查询返回为一个非负整数的情况)
拉普拉斯机制定义为 ,其中
是对数据库
的真实计数查询,
是概率分布为拉普拉斯分布的随机变量,拉普拉斯分布为
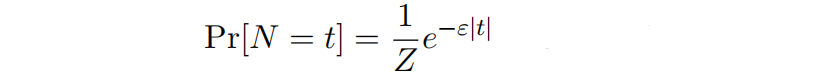
其中 是整数,
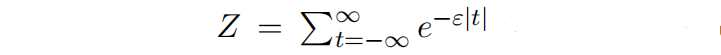
是归一化系数。
这个机制正是第一节我们讨论的那个加入噪声的例子,我们就来证明,拉普拉斯机制是ε-差分隐私的。
让 和
为一对只有一行不相同的数据库,由于
是计数查询,所以
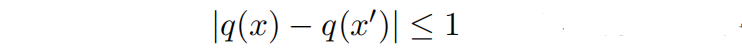
对于每一个 ,
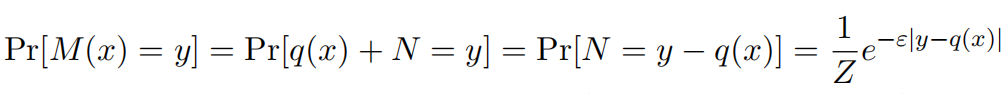
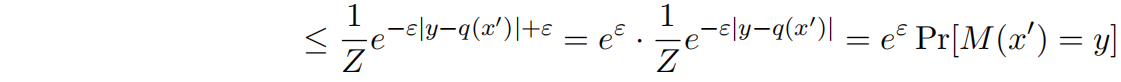
其中上述式子中的不等式使用绝对值不等式公式可以容易得到。
所以,拉普拉斯机制是ε-差分隐私的。
总结
首先通过描述个人隐私泄露的例子,引出了一种加入噪声的保护机制(其实就是拉普拉斯机制)。通过查询前后对单个人数据的认知变化,开始形式化地定义语义隐私、差分隐私,以及两种隐私的关系,最后,正式介绍在计数查询上的拉普拉斯机制,以及证明了拉普拉斯机制就是满足ε-差分隐私的。后续,我们将更加充分和正式地开始对差分隐私进行探讨。
参考
https://zhuanlan.zhihu.com/p/402402476
- ^The Algorithmic Foundations of Differential Privacy https://www.cis.upenn.edu/~aaroth/Papers/privacybook.pdf
- ^abhttp://www.cse.cuhk.edu.hk/~andrejb/csci5520/