树:有n(n>=0)个节点的有限集合 ,n=0时为空树,n=1只有一个根节点,n>1有子节点的树
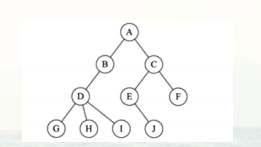
子树:B C 是A的子树,D是B的子树
根节点:A是树的根节点,一个树最多只有一个根节点
度:拥有子节点的个数。A的度为2,B的度为1
树的层次:A是在第一层,G在第四层
注:树最多只有一个根节点,一个子节点最多只有一个父节点。同一层的节点不会相交的
一个树的存储结构:树可以用顺序存储和链式存储。具体用那种看树的复杂度
树的关系比较复杂时使用链式存储。
链式存储的种类:
双亲表示法:存储节点的数据和父节点的地址,这种存储方式找父节点方便,不能找子节点

孩子表示法:存储节点自己的数据和他的子节点的地址,寻找子节点方便,找不到父节点,比较浪费资源

孩子兄弟表示法:存储自己的数据和左节点和自己右边的兄弟。,节省的存储空间

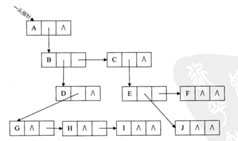
二叉树:每个节点最多有2和子节点称为二叉树
满二叉树:除了最后一层,其他层的节点的都是有两个节点。

完全二叉树:在满二叉树的基础上,最后一层可以少一些叶子节点,但少的节点的位置只能从最后一层的右边开始,少的子节点必须要连续。
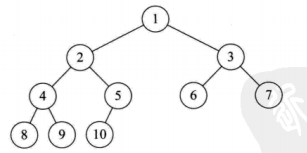
二叉树的一些性质:
1:二叉树的第N层最多有2^(n-1)个节点
2:深度为K的二叉树,整个二叉树的节点数为2^n-1个节点
3:一个二叉树有N个节点,第一个节点为1,把节点按循序排列,第i个节点的父节点为i/2
第n个节点的左节点为2n,右节点为2n+1;
2n>N则该节点没左节点,2n+1>N没有右节点
二叉树的存储:一般根据数的复杂度来确定,不过二叉树一般用顺序存储。因为二叉树一般结构比较简单。
顺序存储:把节点按满二叉树给每个节点编号,即使没这个节点也标号,把这些节点按编号存储到数组中,空节点对应的数组存储的是空节点。
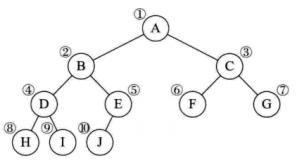

如果使用链式存储二叉树
把节点的数据存储起来,在存储该节点的左节点和右节点的地址信息
二叉树的四种遍历方法:
前序遍历:先访问当前节点,在访问左节点在访问右节点。
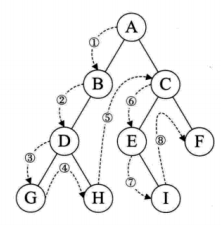
访问顺序:A B D G H C E I F
中序遍历:先遍历访问左节点在访问自身在访问右节点
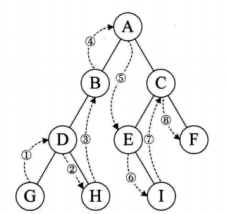
访问顺序:G D H B A E I C F
后序遍历:先遍历访问左节点在遍历访问右节点,最后输出当前节点。
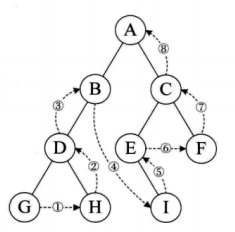
访问顺序:G H D B I E F C A
层序遍历:一层一层从上往下遍历,同一层从左往右遍历。
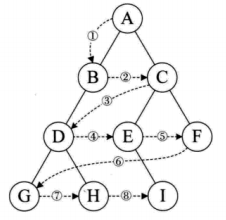
遍历:A B C D E F G H I
使用顺序存储存储数据之间关系为二叉树结构的数据
一般我们数据的结构为满二叉树或完全二叉树时我们使用顺序存储这些数据:把所有的节点按顺序编号,按编号顺序存入数组中,实现顺序存储。
一些普通的二叉树我们也使用顺序存储来存储这些数据,具体实现:把普通二叉树转化成完全二叉树,空节点也要编号,空节点用1代替数据,按顺序把所有的节点编号,按编号把数据存储到数组中,实现数据的顺序存储。
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace EndTraverTree { class Program { //数据之间的关系是二叉树结构,现在我们把二叉树结构的数据按顺序存储,为了用顺序存储我们需要把二叉树补成满二叉树或完全二叉树,空节点的数据设为1 static void Main(string[] args) { //假设数据是字符型,数据之间的关系是二叉树结构,为了用顺序存储我们把二叉树转换成完全二叉树 char[] tree = new char[] { 'A','B','C','D','E','1','F','1','G','H','1','1','1','1','N'}; iTree<char> Tree = new iTree<char>(tree.Length); for (int i = 0; i < tree.Length; i++)//把数据存储到二叉树结构的类中 { Tree.Add(tree[i]); } Tree.EndTree();//对二叉树的数据进行后续遍历 Tree.Layer();//对二叉树的数据进行层序遍历 Console.ReadKey(); } } }
namespace EndTraverTree { public class iTree<T> { private T[] data; private int count = 0; /// <summary> /// 构造函数,再构造这个对象时设置重载的 /// </summary> /// <param name="capacity"></param> public iTree(int capacity) { data = new T[capacity];//在创建这个对象时,用重载确定二叉树数组的大小。 } /// <summary> /// 空的构造函数 /// </summary> public iTree() { } /// <summary> /// 把数据按顺序存储到二叉树中 /// </summary> /// <param name="item"></param> /// <returns></returns> public bool Add(T item) { if(count>=data.Length) { return false; } data[count] = item; count++; return true; } }
使用顺序存储的二叉树的四种遍历方式
顺序存储二叉树的前序遍历
public void first() { FristTree(0); } /// <summary> /// 前序遍历二叉树,使用分治算法 /// </summary> /// <param name="index"></param> private void FristTree(int index) { if (index >= data.Length || data[index].Equals('1')) { return; } int number = index + 1;//当前节点的编号 int LeftNumber = number * 2;//左节点的编号 int RightNumber = number * 2 + 1;//右节点的编号 Console.WriteLine(data[index]); FristTree(LeftNumber - 1); FristTree(RightNumber - 1); }
顺序存储二叉树的中序遍历
public void MiddleTree() { Middle(0); } /// <summary> /// 中序遍历二叉树,使用分治算法 /// </summary> /// <param name="index"></param> private void Middle(int index) { if (index >= data.Length || data[index].Equals('1')) { return; } int number = index + 1;//当前节点的编号 int LeftNumber = number * 2;//左节点的编号 int RightNumber = number * 2 + 1;//右节点的编号 Middle(LeftNumber - 1); Console.WriteLine(data[index]); Middle(RightNumber - 1); }
顺序存储二叉树的后序遍历
public void EndTree()
{
EndTree(0);
}
/// <summary>
/// 后序遍历二叉树,使用分治算法
/// </summary>
/// <param name="index"></param>
private void EndTree(int index)
{
if (index >= data.Length || data[index].Equals('1'))
{
return;
}
int number = index + 1;//当前节点的编号
int LeftNumber = number * 2;//左节点的编号
int RightNumber = number * 2 + 1;//右节点的编号
EndTree(LeftNumber - 1);
EndTree(RightNumber - 1);
Console.WriteLine(data[index]);
{
EndTree(0);
}
/// <summary>
/// 后序遍历二叉树,使用分治算法
/// </summary>
/// <param name="index"></param>
private void EndTree(int index)
{
if (index >= data.Length || data[index].Equals('1'))
{
return;
}
int number = index + 1;//当前节点的编号
int LeftNumber = number * 2;//左节点的编号
int RightNumber = number * 2 + 1;//右节点的编号
EndTree(LeftNumber - 1);
EndTree(RightNumber - 1);
Console.WriteLine(data[index]);
}
顺序存储二叉树的层序遍历
/// <summary> /// 二叉树的层序遍历 /// </summary> public void Layer() { for (int i = 0; i < data.Length; i++) { if(data[i].Equals('1'))//判断是否为空节点,空节点就跳过 { continue; } Console.WriteLine(data[i]);//按层序遍历输出所有不为空的节点 } }
使用链式存储存储数据之间关系为二叉树结构的数据
一般的二叉树可以使用顺序存储也可以使用链式存储,使用链式存储我们的每个节点要存储数据的值以及数据的左右子树和节点的父节点。
二叉排序树类型的数据是一定要用链式存储的
二叉排序树:所有的左节点值要小于他的父节点,有右节点的值要大于他的父节点
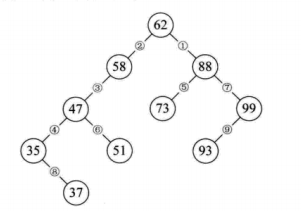
二叉排序树的优点:查找数据方便,数据的排序也方便,插入也方便。
数据的结构是二叉排序树使用链式存储用代码实现:使用整型数据举列
使用代码实现二叉排序树的链式存储:
在二叉排序树的链式存储中增加数据,查找数据,按大小输出数据,删除数据。
增加数据:根据二叉排序树的特点判断要添加的数据是那个节点的左或右节点,在链式表中设置这两个节点的关系。
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace Doubletree { class Program { static void Main(string[] args) { BiTree bitree = new BiTree(); int[] tree = new int[] { 62,58,88,47,73,99,35,51,93,37}; //将一个数据存储到一个节点上,bitree类是把节点按二叉排序结构来构造各个节点之间的关系 foreach (var item in tree) { bitree.Add(item); } } } } using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace Doubletree { /// <summary> /// 这里的数据是二叉排序树结构使用链式存储时,每个节点要存储的信息用BiNode这个类来存储 /// </summary> public class BiNode { //为了安全,将链表中的每个节点的parent RightChild LeftChild date等数据设为属性,保护这些值 //date是存储这个节点的数据的,parent属性是存储这个节点的父节点的地址的, RightChild属性是存储这个节点的右节点的地址的,LeftChild是存储这个节点的左节点的地址的 private BiNode parent = null; private BiNode RightChild = null; private BiNode leftChild = null; private int date = 0; public BiNode Parent { get { return parent; } set { parent = value; } } public BiNode RightChild1 { get { return RightChild; } set { RightChild = value; } } public BiNode LeftChild { get { return leftChild; } set { leftChild = value; } } public int Date { get { return date; } set { } } /// <summary> /// 创建一个构造函数,方便给类传入Date值 /// </summary> /// <param name="item"></param> public BiNode(int item) { date = item; } /// <summary> /// 类中必须有一个空构造函数 /// </summary> public BiNode() { } } } using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace Doubletree { public class BiTree { private BiNode root = null; /// <summary> /// 设置每个节点之间的关系(父节点,左节点,右节点)判断各个节点放置的位置 /// </summary> /// <param name="item"></param> public void Add(int item) { BiNode node = new BiNode(item);//创建一个节点,把数据用构造函数存储再节点中 //判断这个节点用二叉排序树结构放置的位置 if (root == null) { root = node;//如果根节点为空,将该节点设为根节点 } else//根节点不为空,查找该节点与别的节点之间的关系,是否为父节点。。。。。 { BiNode temp = root; while (true) { //数据之间的结构按二叉排序结构构造各个节点之间的关系 if (node.Date >= temp.Date)//大于父节点的子节点放在父节点的右边 { if (temp.RightChild1 == null)//判断右子树是否为空,空就把节点的地址存储到父节点的右子树变量上,以后用父节点的右子树变量就能访问到该节点 { temp.RightChild1 = node;//将子节点的地址存放在父节点的RightChild变量上,利用父节点的RightChild变量能访问子节点 node.Parent = temp;//将父节点的地址存储到子节点的Parent上,以后用该节点的parent变量能访问到父节点 break; } else { temp = temp.RightChild1; } } else//小于父节点的子节点放在父节点的左边,其他的同上 { if (temp.LeftChild == null) { temp.LeftChild = node; node.Parent = temp; break; } else { temp = temp.LeftChild; } } } } } }
查找数据 :判断要查找的值是否为该节点的值,不是就判断要查找的数据在该节点的左边或右边,如果该节点已是叶子节点还不是要找的值就判定要查找的值不再这个二叉树中
//查找用链式存储的二叉树的是否有该数据,有返回Tree没有返回False public void Find(int index)//传入要查找的数据 { bool istrue= Find(index, root); Console.WriteLine(istrue); } /// <summary> /// 从链式存储的二叉树tree中查找Index值 /// </summary> /// <param name="index"></param> /// <param name="tree"></param> /// <returns></returns> private bool Find(int index, BiNode tree) { if(index==tree.Date)//判断根节点是否为要查找的值 { return true; } else { //再二叉树的左右子树中查找传入的值 BiNode temp = tree; while(true) { if(index>temp.Date)//判断要查找的值在这个节点的右边 { if (temp.RightChild1 == null)//判断该节点是否为叶子节点,是叶子节点时,前面已知这个节点不是要查找的值,结束查找,返回查找的结果 { return false; } if (index==temp.RightChild1.Date)//如果这个节点的右节点是要查找的值,返回要查找的结果 { return true; } else//继续查找该节点的右节点的值与要查找的值的大小,用来判断要查找的值在该节点右节点的左右位置 { temp = temp.RightChild1;//判断下一个节点的左右节点是否为要查找的值 } } else if(index<temp.Date)//判断要查找的值在这个节点的左边 { if (temp.LeftChild == null)//同上 { return false; } if (index == temp.LeftChild.Date) { return true; } else { temp = temp.LeftChild; } } } } }
这里有一个优化的查找的方法
public bool OptimizerFind(int index) { BiNode temp = root; while (true) { if(temp==null)//该节点为空,则该值不再二叉排序树中,返回要查找的结果 { return false; } if (index == temp.Date)//该节点的值为要查找的值,返回查找结果 { return true; } if (index > temp.Date)//判断要查找的值在该节点的右子树中,在把该节点的右子节点与该值比较 { temp = temp.RightChild1;//对该节点的右节点进行判断循环 } else//判断要查找的值在该节点的左子树中,在把该节点的左子节点与该值比较 { temp = temp.LeftChild; } } }
按大小输出数据:按二叉排序树结构存储的数据他的中序遍历就可以把树中的数据从小到大输出。
public void InOrderTraverspl() { InOrderTraverspl(root); } /// <summary> /// 将链式存储的数据按中序遍历输出,因为是二叉排序树,所有中序遍历出的数据是按从小到大的顺序输出的 /// </summary> /// <param name="tree"></param> public void InOrderTraverspl(BiNode tree) { if(tree==null) { return; } InOrderTraverspl(tree.LeftChild); Console.WriteLine(tree.Date); InOrderTraverspl(tree.RightChild1); }
删除数据:删除数据分三种情况
第一删除的节点是叶子节点
第二删除的节点只有一个子节点
第三删除的节点有左右两个节点
一般满二叉树和完全二叉树使用顺序存储是方便查找它的父节点和子节点的,但一般二叉树使用顺序存储不方便查找父子节点,我们可以将二叉树构造成完全二叉树在使用顺序存储,但如果构造成完全二叉树需要浪费很多节点时,我们就把该二叉树结构的数据使用链式存储,存储这个节点的数据和父子节点的地址,以便以后查找。对于二叉排序树我们一般使用链式存储。
一般的二叉树使用链式存储时:我们也是把二叉树构造成完全二叉树,在把二叉树用链式存储起来,再把空节点删除。
