dp

题目描述

1191:棋盘分割
查看提交统计提示提问
总时间限制: 1000ms 内存限制: 65536kB
描述
将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

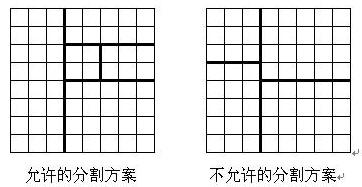
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的均方差最小。
均方差，其中平均值，xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n，求出O'的最小值。
输入
第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
输出
仅一个数，为O'（四舍五入精确到小数点后三位）。
样例输入
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
样例输出
1.633
来源
Noi 99

解题思路

一块棋盘一共有四种分割方式，竖着切然后一遍保留继续切，一边切掉，横着切，一边保留，一边切掉，对保留下来的那块棋盘，继续做同样的工作。

解题代码

#include <cstdio>
#include <cmath>
#include <cstring>

int board[9][9];
int sum[9][9];
int res[15][9][9][9][9];

int CalSum(int x1, int y1, int x2, int y2){
    return sum[x2][y2] + sum[x1-1][y1-1] - sum[x1-1][y2] - sum[x2][y1-1];
}

int min(int a, int b){
    return a < b ? a: b;
}

int Fanc(int n, int x1, int y1, int x2, int y2){
    
    int minf = 10000000;
    if(res[n][x1][y1][x2][y2] != -1)
        return res[n][x1][y1][x2][y2];
    if(n == 1){
        int temp = CalSum(x1, y1, x2, y2);
        res[n][x1][y1][x2][y2] = temp * temp;
        return temp * temp;
    }
    for(int i = x1; i < x2; i++){
        int left = CalSum(x1, y1, i, y2);
        int right = CalSum(i+1, y1, x2, y2);
        int temp = min(Fanc(n-1, x1, y1, i, y2) + right * right , Fanc(n-1, i+1, y1, x2, y2) + left * left);
        minf = min(minf, temp);
    }
    for(int j = y1; j < y2; j++){
        int up = CalSum(x1, y1, x2, j);
        int down = CalSum(x1, j+1, x2, y2);
        int temp = min(Fanc(n-1, x1, j+1, x2, y2) + up * up, Fanc(n-1, x1, y1, x2, j) + down * down);
        minf = min(minf, temp);
    }
    res[n][x1][y1][x2][y2] = minf;
    return minf;
}

int main(){
    int n;
    memset(sum, 0, sizeof(sum));
    memset(res, -1, sizeof(res));
    scanf("%d", &n);
    for(int i = 1; i < 9; i++){
        for(int j = 1, rowSum = 0; j < 9; j++){
            scanf("%d", &board[i][j]);
            rowSum += board[i][j];
            sum[i][j] += sum[i-1][j] + rowSum;
        }
    }
    double ans = n * Fanc(n, 1, 1, 8, 8) - sum[8][8] * sum[8][8];
    printf("%.3f
", sqrt((double)ans / (n*n)));
    return 0;
}