转自:勿在浮沙筑高台http://blog.csdn.net/luoshixian099/article/details/51908175
关于图的几个概念定义:
- 连通图:在无向图中,若任意两个顶点vi与vj都有路径相通,则称该无向图为连通图。
- 强连通图:在有向图中,若任意两个顶点vi与vj都有路径相通,则称该有向图为强连通图。
- 连通网:在连通图中,若图的边具有一定的意义,每一条边都对应着一个数,称为权;权代表着连接连个顶点的代价,称这种连通图叫做连通网。
- 生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
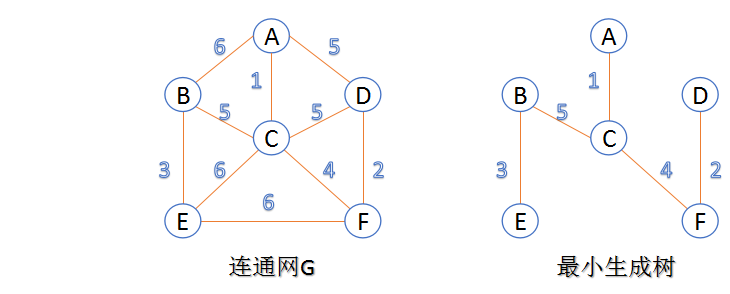
- 最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。
下面介绍两种求最小生成树算法
Kruskal算法
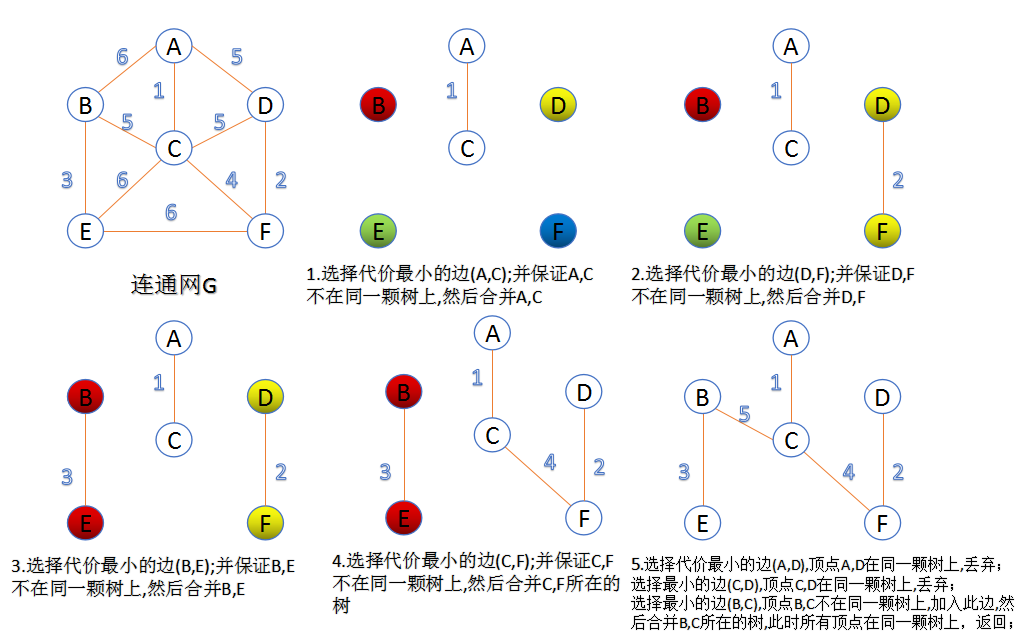
此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
1. 把图中的所有边按代价从小到大排序;
2. 把图中的n个顶点看成独立的n棵树组成的森林;
3. 按权值从小到大选择边,所选的边连接的两个顶点ui,vi应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
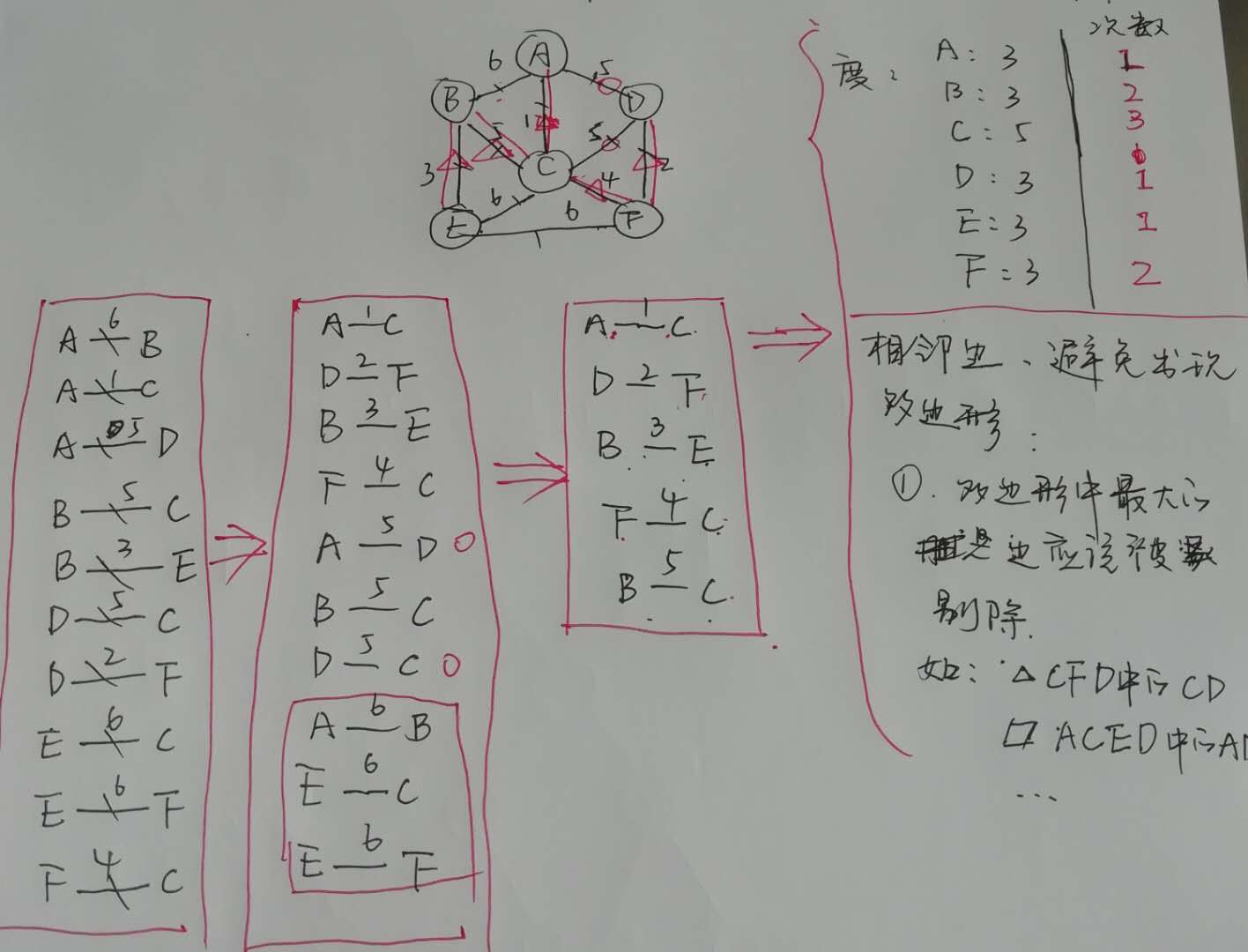
简单证明Kruskal算法
数学归纳法:对图的顶点数n做归纳,证明Kruskal算法对任意n阶图适用。
归纳基础:
- n=1,显然能够找到最小生成树(即本身)。
归纳过程:
- 假设Kruskal算法对n≤k阶图适用,那么,在k+1阶图G中,我们把最短边的两个端点a和b做一个合并操作,即把u与v合为一个点v',把原来接在u和v的边都接到v'上去,这样就能够得到一个k阶图G'(u,v的合并是k+1少一条边),G'最小生成树T'可以用Kruskal算法得到
- 我们证明T'+{<u,v>}是G的最小生成树
- 用反证法,如果T'+{<u,v>}不是最小生成树,最小生成树是T,即W(T)<W(T'+{<u,v>})。显然T应该包含<u,v>,否则,可以用<u,v>加入到T中,形成一个环,删除环上原有的任意一条边,形成一棵更小权值的生成树。而T-{<u,v>},是G'的生成树。所以W(T-{<u,v>})<=W(T'),也就是W(T)<=W(T')+W(<u,v>)=W(T'+{<u,v>}),产生了矛盾。于是假设不成立,T'+{<u,v>}是G的最小生成树,Kruskal算法对k+1阶图也适用
- 由数学归纳法,Kruskal算法得证
Prim算法
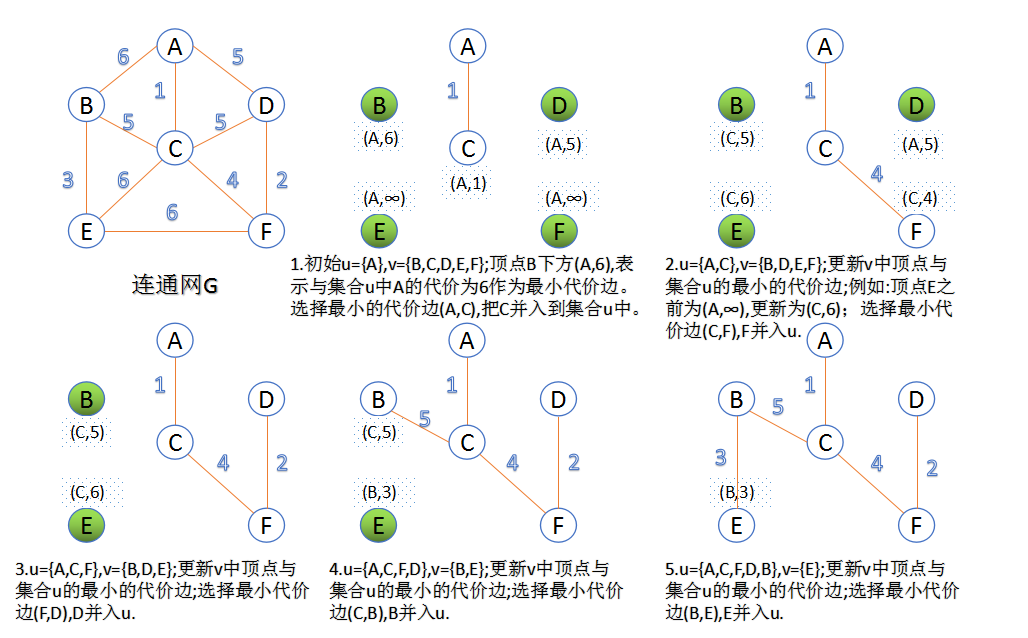
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
- 图的所有顶点集合为V;初始令集合u={s},v=V−u;
- 在两个集合u,v能够组成的边中,选择一条代价最小的边(u0,v0),加入到最小生成树中,并把v0并入到集合u中。
- 重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。
由于不断向集合u中加点,所以最小代价边必须同步更新;需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息,:
struct { char vertexData //表示u中顶点信息 UINT lowestcost //最小代价 }closedge[vexCounts]
简单证明prim算法
反证法:假设prim生成的不是最小生成树(替换法—与最优子结构证明相似)
- 设prim生成的树为G0
- 假设存在Gmin使得cost(Gmin)<cost(G0) 则在Gmin中必定存在<u,v>不属于G0
- 将<u,v>加入G0中可得一个环,且<u,v>不是该环的最长边(这是因为<u,v>∈Gmin)
- 这与prim每次生成最短边矛盾
- 故假设不成立,命题得证
完整代码

#include <iostream> #include <vector> #include <queue> #include <algorithm> using namespace std; #define INFINITE 0xFFFFFFFF #define VertexData unsigned int //顶点数据 #define UINT unsigned int #define vexCounts 6 //顶点数量 char vextex[] = { 'A', 'B', 'C', 'D', 'E', 'F' }; struct node { VertexData data; unsigned int lowestcost; }closedge[vexCounts]; //Prim算法中的辅助信息 typedef struct { VertexData u; VertexData v; unsigned int cost; //边的代价 }Arc; //原始图的边信息 void AdjMatrix(unsigned int adjMat[][vexCounts]) //邻接矩阵表示法 { for (int i = 0; i < vexCounts; i++) //初始化邻接矩阵 for (int j = 0; j < vexCounts; j++) { adjMat[i][j] = INFINITE; } adjMat[0][1] = 6; adjMat[0][2] = 1; adjMat[0][3] = 5; adjMat[1][0] = 6; adjMat[1][2] = 5; adjMat[1][4] = 3; adjMat[2][0] = 1; adjMat[2][1] = 5; adjMat[2][3] = 5; adjMat[2][4] = 6; adjMat[2][5] = 4; adjMat[3][0] = 5; adjMat[3][2] = 5; adjMat[3][5] = 2; adjMat[4][1] = 3; adjMat[4][2] = 6; adjMat[4][5] = 6; adjMat[5][2] = 4; adjMat[5][3] = 2; adjMat[5][4] = 6; } int Minmum(struct node * closedge) //返回最小代价边 { unsigned int min = INFINITE; int index = -1; for (int i = 0; i < vexCounts;i++) { if (closedge[i].lowestcost < min && closedge[i].lowestcost !=0) { min = closedge[i].lowestcost; index = i; } } return index; } void MiniSpanTree_Prim(unsigned int adjMat[][vexCounts], VertexData s) { for (int i = 0; i < vexCounts;i++) { closedge[i].lowestcost = INFINITE; } closedge[s].data = s; //从顶点s开始 closedge[s].lowestcost = 0; for (int i = 0; i < vexCounts;i++) //初始化辅助数组 { if (i != s) { closedge[i].data = s; closedge[i].lowestcost = adjMat[s][i]; } } for (int e = 1; e <= vexCounts -1; e++) //n-1条边时退出 { int k = Minmum(closedge); //选择最小代价边 cout << vextex[closedge[k].data] << "--" << vextex[k] << endl;//加入到最小生成树 closedge[k].lowestcost = 0; //代价置为0 for (int i = 0; i < vexCounts;i++) //更新v中顶点最小代价边信息 { if ( adjMat[k][i] < closedge[i].lowestcost) { closedge[i].data = k; closedge[i].lowestcost = adjMat[k][i]; } } } } void ReadArc(unsigned int adjMat[][vexCounts],vector<Arc> &vertexArc) //保存图的边代价信息 { Arc * temp = NULL; for (unsigned int i = 0; i < vexCounts;i++) { for (unsigned int j = 0; j < i; j++) { if (adjMat[i][j]!=INFINITE) { temp = new Arc; temp->u = i; temp->v = j; temp->cost = adjMat[i][j]; vertexArc.push_back(*temp); } } } } bool compare(Arc A, Arc B) { return A.cost < B.cost ? true : false; } bool FindTree(VertexData u, VertexData v,vector<vector<VertexData> > &Tree) { unsigned int index_u = INFINITE; unsigned int index_v = INFINITE; for (unsigned int i = 0; i < Tree.size();i++) //检查u,v分别属于哪颗树 { if (find(Tree[i].begin(), Tree[i].end(), u) != Tree[i].end()) index_u = i; if (find(Tree[i].begin(), Tree[i].end(), v) != Tree[i].end()) index_v = i; } if (index_u != index_v) //u,v不在一颗树上,合并两颗树 { for (unsigned int i = 0; i < Tree[index_v].size();i++) { Tree[index_u].push_back(Tree[index_v][i]); } Tree[index_v].clear(); return true; } return false; } void MiniSpanTree_Kruskal(unsigned int adjMat[][vexCounts]) { vector<Arc> vertexArc; ReadArc(adjMat, vertexArc);//读取边信息 sort(vertexArc.begin(), vertexArc.end(), compare);//边按从小到大排序 vector<vector<VertexData> > Tree(vexCounts); //6棵独立树 for (unsigned int i = 0; i < vexCounts; i++) { Tree[i].push_back(i); //初始化6棵独立树的信息 } for (unsigned int i = 0; i < vertexArc.size(); i++)//依次从小到大取最小代价边 { VertexData u = vertexArc[i].u; VertexData v = vertexArc[i].v; if (FindTree(u, v, Tree))//检查此边的两个顶点是否在一颗树内 { cout << vextex[u] << "---" << vextex[v] << endl;//把此边加入到最小生成树中 } } } int main() { unsigned int adjMat[vexCounts][vexCounts] = { 0 }; AdjMatrix(adjMat); //邻接矩阵 cout << "Prim :" << endl; MiniSpanTree_Prim(adjMat,0); //Prim算法,从顶点0开始. cout << "-------------" << endl << "Kruskal:" << endl; MiniSpanTree_Kruskal(adjMat);//Kruskal算法 return 0; }